By my99n — May 22, 2025

Category Theory คืออะไร แค่มีกลม ๆ กับลูกศรก็ใช่แล้วหรอ

นักคณิตศาสตร์มักหมกมุ่นกับการทำให้ความหมายของสิ่งต่าง ๆ นั้น 'ทั่วไป' มากขึ้น

นึกภาพคล้าย ๆ กับการที่เวลาพูดคำว่าผลไม้ คนทั่วไปก็อาจจะนึกถึงพวกแอปเปิ้ล มะละกอ กล้วย หรือส้ม แต่ถ้าเราขยายความหมายของคำว่าผลไม้ออกไปในทางชีววิทยาที่ว่า 'ส่วนของพืชที่พัฒนาแล้วจากรังไข่ของดอกไม้และมีหน้าที่ในการแพร่พันธุ์เมล็ด' แล้วล่ะก็ มะเขือเทศ พริก ฟักทอง หรือแตงกวา ก็จะต้องนับว่าเป็นผลไม้ด้วย

นักคณิตศาสตร์ก็ชอบทำอะไรประมาณนี้เช่นกัน เพียงแต่ไม่ได้ทำกับสิ่งของที่จับต้องได้ทั่วไป แต่ทำกับวัตถุในโลกคณิตศาสตร์มากกว่า

อย่างคำว่า 'เวกเตอร์' ที่เราเรียนในชั้นมัธยมว่าหมายถึงปริมาณที่มีทั้งขนาดและทิศทาง เขียนแทนได้ด้วยหัวลูกศรหรือคู่อันดับ นักคณิตศาสตร์พบว่าเวกเตอร์นั้นมีสมบัติที่น่าสนใจซึ่งลิสท์ออกมาได้ 10 ข้อ ยกตัวอย่างเช่น สมบัติสลับที่การบวก หรือสมบัติการกระจายการคูณสเกล่าเข้าไปในผลบวกของเวกเตอร์ เป็นต้น

แล้วนักคณิตศาสตร์ก็สังเกตว่านอกจากเวกเตอร์ที่เป็นหัวลูกศรแล้ว วัตถุอื่น ๆ ในคณิตศาสตร์อย่างเมทริกซ์ พหุนาม ลำดับ หรือแม้แต่ฟังก์ชัน ก็มีสมบัติ 10 ข้อที่ว่านี้เช่นกัน นักคณิตศาสตร์เลยบอกว่า โอเค งั้นนิยามใหม่ เราจะเรียกอะไรก็ตามที่มีสมบัติครบ 10 ข้อนั้นว่าเวกเตอร์หมดเลย และมองว่าเวกเตอร์ลูกศรที่เรารู้จักตอนเด็ก ๆ นั้นเป็นแค่กรณีเฉพาะของเวกเตอร์ในความหมายใหม่เท่านั้น

พอเราทำแบบนี้ แค่เราศึกษาเกี่ยวกับเวกเตอร์ ก็เท่ากับเราศึกษาเมทริกซ์ พหุนาม ลำดับ ไปพร้อม ๆ กัน ทฤษฎีที่เราได้นอกจากจะใช้ได้กับเวกเตอร์ที่เป็นลูกศร ก็ยังใช้ได้กับพหุนาม หรือวัตถุทางคณิตศาตร์อะไรก็ตามที่มีสมบัติ 10 ข้อนั้นด้วย ยิงปืนนัดเดียวได้นกหลายตัว

ในวิชาอื่น ๆ ก็ชอบทำประมาณนี้แหละครับ กรุปในวิชาพีชคณิตนามธรรม หรือปริภูมิเชิงโทโพโลจีในวิชาโทโพโลจี ก็เช่นกัน พวกมันคือการพยายามหานิยามบางอย่างมาครอบวัตถุทางคณิตศาสตร์หลาย ๆ อย่างที่มีสมบัติบางประการร่วมกันนั่นเอง

ทุกอย่างควรจะจบลงตรงนี้ คือตรงที่แต่ละวิชาก็ได้คอนเซ็ปทั่วไปบางอย่าง แล้วก็ศึกษาคอนเซ็ปนั้นในแง่มุมของตัวเอง สร้างทฤษฎีของเวกเตอร์ ของกรุป ของโทโพโลยี แต่กลับมีนักคณิตศาสตร์หัวใสรู้สึกตะหงิด ๆ ว่า ไอ้เจ้าคอนเซ็ปทั่วไปในแต่ละสาขาของคณิตศาสตร์เนี่ย มันมีส่วนที่คล้าย ๆ กันอยู่นะ คือมันมีก้อนอะไรสักอย่าง กับสิ่งที่ส่งก้อน ๆ นึงไปอีกก้อนหนึ่ง

อย่างในวิชาพีชคณิตเชิงเส้นนั้นมีการแปลงเชิงเส้นที่ส่งจากปริภูมิเวกเตอร์นึงไปหาอีกอันนึง กรุปก็ส่งหากันด้วยโฮโมมอร์ฟิซึม ปริภูมิเชิงโทโพโลจีก็มีฟังก์ชันต่อเนื่องไว้ใช้ส่ง จนเกิดเป็นความคิดที่ว่า หรือจริง ๆ แล้วเรามีแค่ทฤษฎีของคณิตศาสตร์อันเดียวพอ ไม่ต้องมีทฤษฎีของเวกเตอร์ ของกรุป ของโทโพโลยี แยกกัน

ใช่ครับ นั่นคือไอเดียหลักของวิชา Category Theory

Category Theory คือการพยายามสร้างคอนเซปทั่วไปของคอนเซปทั่วไปอีกที นั่นคือจากที่เรามองว่าแต่ละปริภูมิเวกเตอร์นั้นส่งหากันด้วยการแปลงเชิงเส้น มองกรุปว่าส่งหากันด้วยโฮโมมอร์ฟิซึม มองปริภูมิเชิงโทโพโลยีว่าถูกส่งหากันด้วยฟังก์ชันต่อเนื่อง เรามองของพวกนั้นเป็นก้อนอะไรสักอย่าง แทนด้วยสัญลักษณ์วงกลม แล้วแทนการส่งจากก้อนนึงไปอีกหาอีกก้อนนึงด้วยลูกศร และเรียกวงกลม ๆ กับลูกศรพวกนี้รวมว่า category

ซึ่งพอพูดแบบนี้ มันอาจจะฟังดูเหมือนว่าเราเอาอะไรมาวาด ๆ แล้วโยงลูกศรก็กลายเป็น category หมดเลยสิ แต่จริง ๆ แล้วไม่ใช่ครับ เพราะ category ไม่ใช่ก้อนกับลูกศรอะไรก็ได้ ก้อนและลูกศรเหล่านั้นต้องสอดคล้องกับเงื่อนไข 3 ข้อที่ว่า

ลูกศรจะต้องต่อกันได้ หมายถึงว่าถ้ามีลูกศร f ที่ลากจาก A ไป B กับลูกศร g ที่ลากจาก B ไป C มันจะมีลูกศรอีกอันนึงจาก A ไป C ที่เหมือนกับการลาก f แล้วลาก g ต่อ เรานิยามให้ ∘ หมายถึงการลากลูกศรต่อเนื่องกัน เช่น g∘f หมายถึงลาก g ต่อจาก f
ก้อนทุกก้อนต้องมีลูกศรเอกลักษณ์ ที่เริ่มลากและกลับมาจบที่ตัวมันเอง โดยลูกศรเอกลักษณ์ของก้อน A มักใช้สัญลักษณ์เป็น id_A หรือ 1_A และถ้าลาก f ต่อจากลูกศรเอกลักษณ์ หรือลากลูกศรเอกลักษณ์ต่อจาก f จะต้องเหมือนกับการลาก f อย่างเดียว นั่นคือ f∘1_A = f และ 1_B∘f = f เมื่อ f เป็นลูกศรจาก A ไป B
การต่อกันของลูกศรนั้นต้องเปลี่ยนกลุ่มได้ นั่นคือ ถ้าเรามีลูกศร f ที่ลากจาก A ไปหา B มีลูกศร g ที่ลากจาก B ไปหา C และลูกศร h ที่ลากจาก C ไปหา D นั่นคือ เราต้องได้ว่าลูกศร h ∘ (g ∘ f) นั้นต้องเท่ากับลูกศร (h ∘ g) ∘ f

ถ้าไม่เป็นไปตามสามข้อนี้ ก็ไม่ถือว่าเป็น category ครับ

รูปข้างล่างคือตัวอย่างของ category ง่าย ๆ ที่มีก้อน 3 ก้อน คือ A B C และมีลูกศร 6 ลูกศร นั่นคือเอกลักษณ์ทั้ง 3 และ f g กับ g∘f

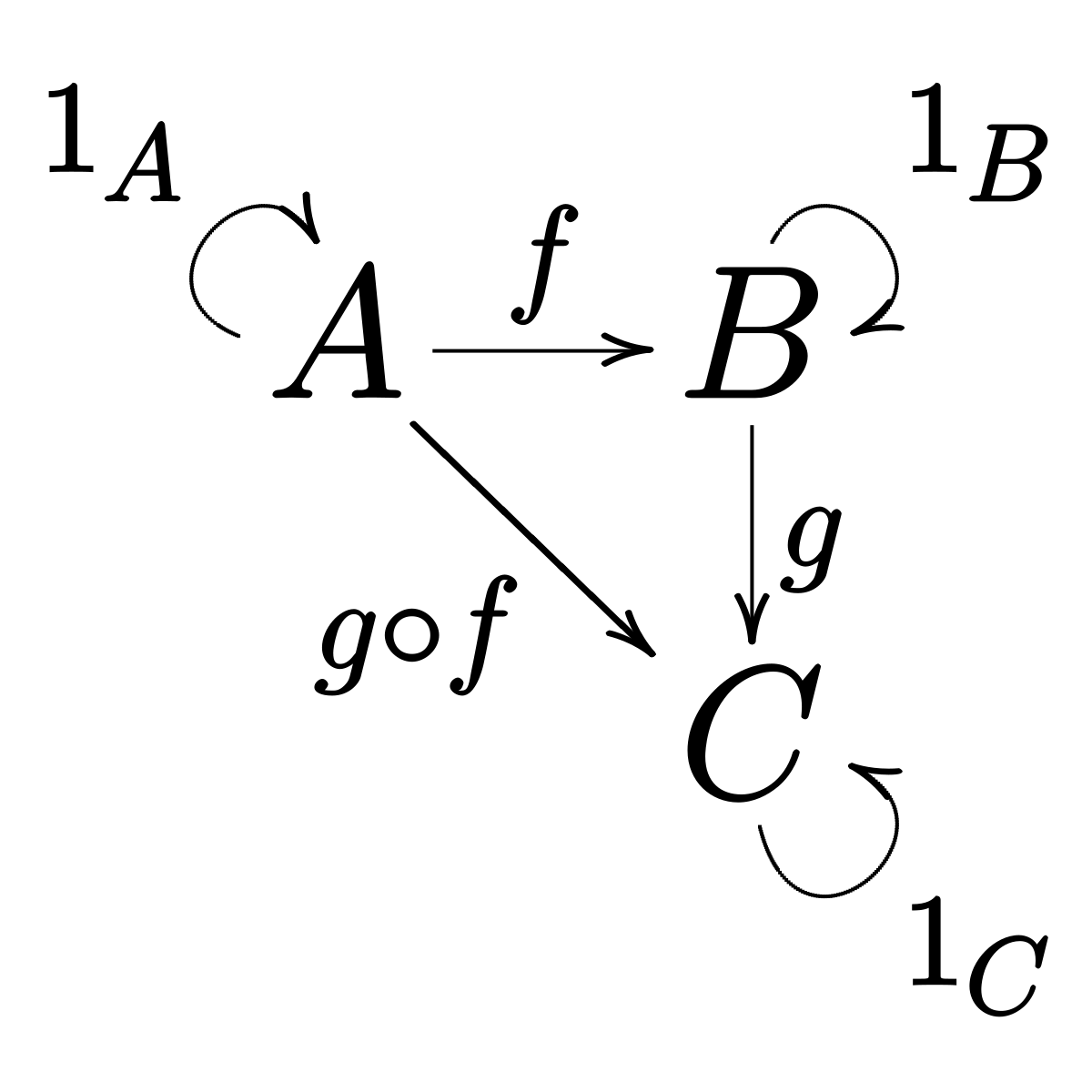
ซึ่งด้วยนิยามนี้ เราจะสามารถสร้าง category ของปริภูมิเวกเตอร์ ของกรุป และของปริภูมิเชิงโทโพโลยีได้ และทฤษฎีอะไรก็ตามที่จริงสำหรับ category มันก็จะไปจริงบนทุกปริภูมิเวกเตอร์ ทุกกรุป และทุกปริภูมิเชิงโทโพโลยีโดยอัตโนมัติ

คราวนี้ไม่ใช่แค่ยิงปืนนัดเดียวได้นกหลายตัวแล้ว แต่เรียกว่าได้นกหลายรังเลยจะเหมาะกว่า

ยกตัวอย่างเช่น เรารู้กันอยู่แล้วว่าตัวดำเนินการหลายตัวในคณิตศาสตร์ นั้นมีสมบัติที่เรียกว่าการมีผลลัพท์เพียงหนึ่งเดียว เช่น ผลคูณของจำนวนจริงสองจำนวน ค่าสูงสุดหรือต่ำสุดของจำนวนจริงสองจำนวน หรือตัวคูณร่วมน้อยและตัวหารร่วมมากของจำนวนเต็มสองจำนวน ซึ่งการพิสูจน์ความมีหนึ่งเดียวของผลลัพท์นี้นั้นก็ต้องใช้เทคนิคเฉพาะต่างกันไปตามแต่ละสาขา

แต่หากเราไปพิจารณาในระดับ category เราสามารถนิยามสิ่งที่เรียกว่า product และพิสูจน์ได้ว่ามันมีหนึ่งเดียวเสมอ เพราะฉะนั้นเราก็สามารถพิสูจน์การมีผลลัพท์เพียงหนึ่งเดียวของตัวดำเนินการต่าง ๆ ได้มากมาย เพียงแค่ต้องหาวิธีนิยามก้อนกับลูกศรที่ทำให้ product ที่ออกมาสอดคล้องกับตัวดำเนินการที่เราสนใจ

ดังนั้นคำพูดของ Eugenia Cheng ที่พูดไว้ว่า Category Theory คือ คณิตศาตร์ของคณิตศาสตร์อีกที จึงเป็นข้อสรุปที่ดีของวิชานี้ เพราะถ้าคณิตศาตร์คือศาสตร์ที่ว่าด้วยการศึกษารูปแบบของสิ่งต่าง ๆ Category Theory ซึ่งพยายามศึกษารูปแบบของวิชาต่าง ๆ ในคณิตศาตร์ก็ควรจะถูกเรียกว่าเป็นคณิตศาตร์ของคณิตศาสตร์อีกที

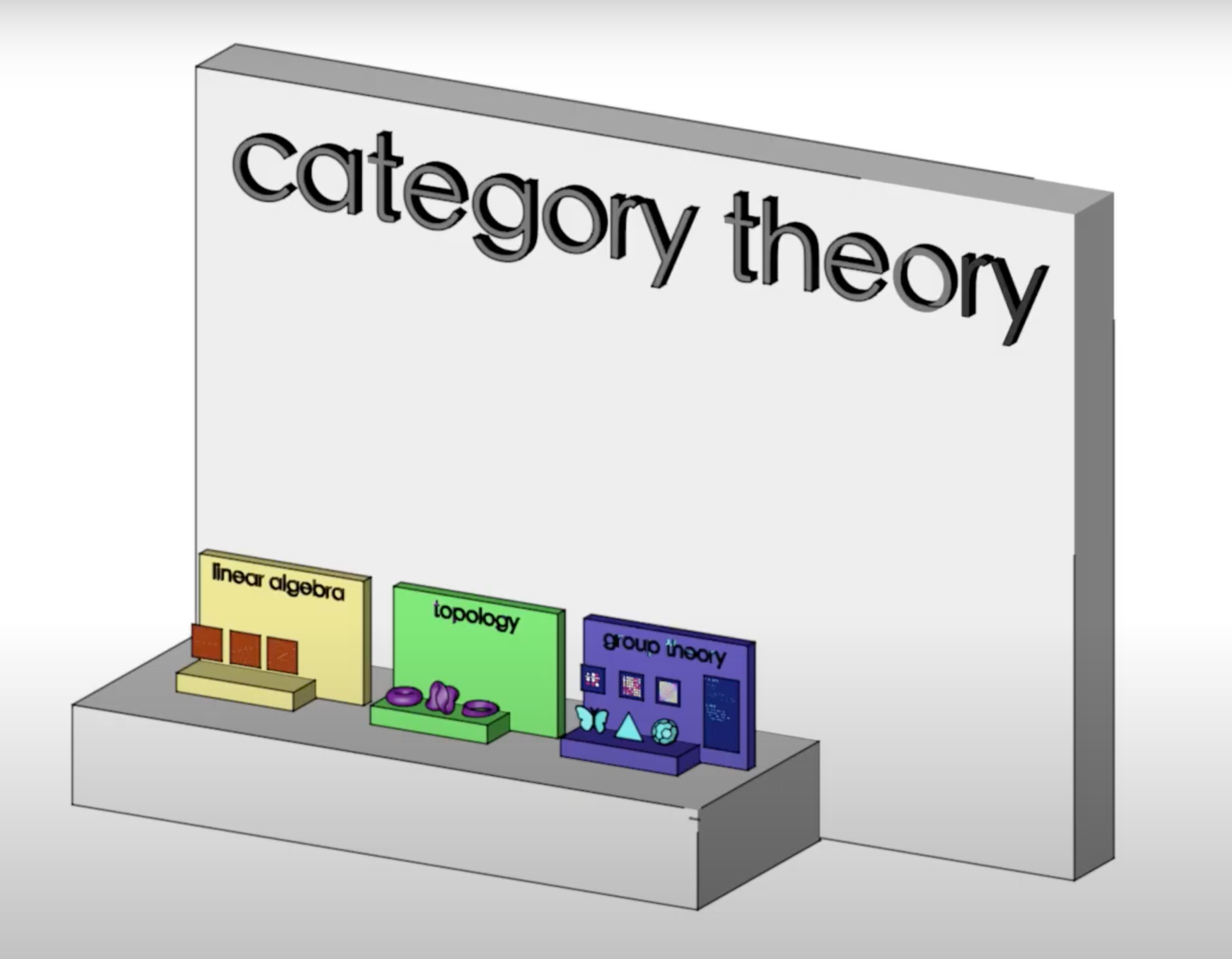
และด้วยความที่ Category Theory พยายามหารูปแบบที่นามธรรมมาก ๆ ในของที่ก็นามธรรมอยู่แล้ว มันเลยถูกเรียกอย่างไม่เป็นทางการอีกชื่อนึงว่าเป็น วิชานามธรรมไร้สาระ

แต่จริง ๆ แล้วมันก็คงไม่ต่างจากคณิตศาสตร์อีกหลายแขนงนั่นแหละครับ ที่ตอนถูกคิดขึ้นมาก็มักจะถูกมองว่าเป็นเรื่องนามธรรมไร้สาระเกินไปเสมอ เพราะตอนนี้วิชา Category Theory ก็เริ่มมีบทบาทสำคัญในหลากหลายสาขา อย่างเช่นในการเขียนโปรแกรมเชิงฟังก์ชัน ซึ่งโปรแกรมเมอร์นำแนวคิดของ Category Theory อย่างฟังก์เตอร์และโมนาดมาใช้เพื่อเขียนโปรแกรมให้ปลอดภัยขึ้นและลดโอกาสเกิดข้อผิดพลาด หรือการออกแบบระบบฐานข้อมูลที่สามารถเชื่อมต่อและทำงานร่วมกันได้ง่ายขึ้นด้วยโครงสร้างในวิชา Category Theory เช่น functor monad และอีกมากมาย

ก็เป็นเรื่องน่าสนใจ ว่าหลังจากนี้เราจะได้เห็น Category Theory ถูกนำไปใช้ในศาสตร์ไหนอีกบ้าง และมันจะยังเป็นแค่วิชานามธรรมไร้สาระไปได้อีกนานแค่ไหน

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

Category Theory คืออะไร แค่มีกลม ๆ กับลูกศรก็ใช่แล้วหรอ

เอกสารอ้างอิง

ใคร ๆ ก็รู้ว่าโดยทั่วไป Decision Tree นั้นดีกว่า Logistic Regression แต่ทำไมล่ะ