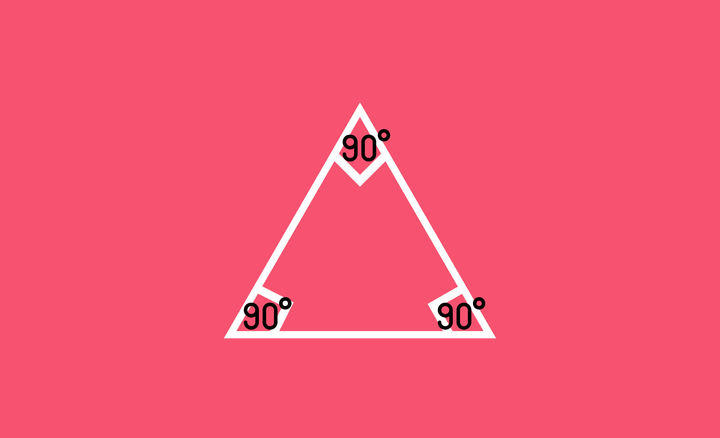
คุณเคยเห็น 7 เหลี่ยมที่ไหนบ้าง

สังเกตไหมครับว่า เราแทบไม่เคยเห็นรูปเจ็ดเหลี่ยมที่ไหนเลย
ลองมองดูของรอบ ๆ ตัวดูก็ได้ คุณจะพบว่าโลกของเรานั้นเต็มไปด้วยรูปร่างเดิม ๆ ซ้ำ ๆ เช่น โทรศัพท์ หนังสือ หรือจอที่คุณใช้อ่านบทความนี้ที่เป็นสี่เหลี่ยม ดาวทะเลที่มักจะมีหน้าตาเป็นห้าเหลี่ยม เกล็ดหิมะและรังผึ้งที่เป็นรูปหกเหลี่ยม หรือป้ายจราจรที่เป็นแปดเหลี่ยม
อ่าว แล้วเจ็ดเหลี่ยมล่ะ
ข้อสันนิษฐานหนึ่งว่าทำไมเราถึงไม่ค่อยเห็นเจ็ดเหลี่ยมก็คือ เพราะมันวาดยาก เอาแค่ถ้าผมบอกให้คุณวาดเจ็ดเหลี่ยมออกมาสักรูป คุณยังต้องนึกอยู่สักพักว่าหน้าตามันควรจะเป็นยังไง ต่างจากรูปสามเหลี่ยม สี่เหลี่ยม ห้าเหลี่ยม หกเหลี่ยม และแปดเหลี่ยมที่ยังพอนึกออก

ถ้ายังจำที่เราเคยเรียนตอนประถมได้ รูปสามเหลี่ยมนั้นมีมุมภายในเท่ากับ 180 องศา รูปสี่เหลี่ยมมีมุมภายในเท่ากับ 360 องศา หรือถ้าพูดในกรณีทั่ว ๆ ไปได้ว่า รูป n เหลี่ยมนั้นจะมีมุมภายในเท่ากับ (n-2) × 180 องศา
หมายความว่าแต่ละมุมของรูป n เหลี่ยมด้านเท่ามุมเท่าจะมีขนาดเท่ากับ (n-2) × 180 / n องศา
ซึ่งเมื่อแทนค่า n เท่ากับ 3 4 5 และ 6 ลงไปจะได้ว่า แต่ละมุมของสามเหลี่ยมด้านเท่ามุมเท่าจะมีขนาดเท่ากับ 60 องศา ของสี่เหลี่ยมเท่ากับ 90 องศา ห้าเหลี่ยมเท่ากับ 108 องศา และหกเหลี่ยมเป็น 120 องศา ซึ่งทุกเลขก็ดูสวยดี จนกระทั่งเมื่อแทนเลข 7 เราจะได้ว่ามุมแต่ละมุมของเจ็ดเหลี่ยมเป็น 128.571428... องศา ซึ่งดูไม่สวยเอาซะเลย

ในยุคกรีกโบราณ นักคณิตศาสตร์เชื่อว่าเราสามารถสร้างรูปเรขาคณิตต่าง ๆ ได้โดยใช้อุปกรณ์พื้นฐานคือวงเวียน และไม้บรรทัดแบบไม่มีสเกลที่เรียกว่าสันตรง ด้วยสองอุปกรณ์นี้ พวกเขาสามารถสร้างรูปร่างต่าง ๆ เช่นสามเหลี่ยม สี่เหลี่ยม ห้าเหลี่ยม และ หกเหลี่ยมได้สำเร็จ แบ่งมุมเป็นสองส่วนเท่า ๆ กัน หรือแม้แต่สร้างสี่เหลี่ยมจัตุรัสที่มีพื้นที่เป็นสองเท่าของรูปเดิมได้ จนเหมือนว่าพวกเขาจะสามารถวาดรูปทุกอย่างได้ด้วยแค่วงเวียนและสันตรงเท่านั้น
แต่ทุกอย่างพังลงที่เจ็ดเหลี่ยม เพราะไม่ว่าจะลองผิดลองถูกอยู่หลายครั้งยังไง พวกเขาก็ยังหาวิธีวาดเจ็ดเหลี่ยมด้านเท่ามุมเท่าไม่ได้เสียที จนเวลาผ่านไปประมาณ 2000 ปี นักคณิตศาสตร์ชาวฝรั่งเศสชื่อคุณ Pierre Wantzel ถึงสามารถพิสูจน์ได้ว่า เราไม่สามารถวาดรูปเจ็ดเหลี่ยมได้ด้วยแค่วงเวียนและสันตรง
นอกจากการวาดรูปเจ็ดเหลี่ยมจะทำได้ยากแล้ว อีกหนึ่งข้อสันนิษฐานที่น่าสนใจก็คือ เหตุผลที่เราไม่ค่อยเห็นรูปเจ็ดเหลี่ยมในชีวิตประจำวัน อาจเป็นเพราะมัน ไม่ค่อยมีประสิทธิภาพในแง่ของการเอามาเรียง
ภาพด้านล่างแสดงให้เห็นว่า รูปสามเหลี่ยม สี่เหลี่ยม และหกเหลี่ยมสามารถนำมาเรียงต่อกันบนระนาบได้แบบไม่มีช่องว่าง หรือเรียกว่า tessellation แต่รูปเจ็ดเหลี่ยมกลับไม่สามารถทำได้แบบนั้น หากผึ้งเลือกสร้างรังเป็นรูปเจ็ดเหลี่ยม แทนที่จะเป็นหกเหลี่ยมอย่างที่เป็นอยู่ในธรรมชาติ มันจะต้องสูญเสียพื้นที่ใช้งานระหว่างช่องถึง ประมาณ 10.8%

ที่มาภาพ: mathartfun, wikipedia
ความลับที่ทำให้สาม สี่ และหกเหลี่ยมด้านเท่าสามารถเอามาเรียงต่อกันจนเต็มพื้นที่ได้อยู่ที่ขนาดของมุมของมัน ซึ่งสามารถเอามาประกอบกันจนได้ 360 องศาพอดี
ดูรูปทางซ้าย แต่ละจุดที่เกิดขึ้นเป็นจุดที่สามเหลี่ยม 6 รูปต่อกัน นั่นก็เพราะว่ามุมแต่ละมุมของสามเหลี่ยมด้านเท่าคือ 60 องศา และ 60 × 6 มันครบ 360 องศาพอดี รูปถัดมาแต่ละจุดจะมีสี่เหลี่ยมต่อกัน 4 ชิ้น เพราะมุมของสี่เหลี่ยมเป็น 90 องศา และ 90 × 4 เท่ากับ 360 พอดี รูปถัดมาอีกก็จะเห็นว่าหกเหลี่ยมมีมุมละ 120 องศา พอเอา 3 อันมาต่อกันเลยได้ 360 องศาพอดี รูปเหล่านี้เลยสามารถเรียงต่อกันได้สนิท
ซึ่งรูปห้าเหลี่ยมหรือเจ็ดเหลี่ยมไม่สามารถปูพื้นได้แบบไม่มีช่องว่าง เพราะห้าเหลี่ยมด้านเท่ามีมุมภายในเท่ากับ 108 องศา และเมื่อนำห้าเหลี่ยมสามรูปมาต่อกันที่มุมเดียวกัน จะได้ผลรวมของมุมเท่ากับ 108 × 3 เท่ากับ 324 ซึ่งยังไม่ถึง 360 องศา จึงทำให้เกิดช่องว่างขึ้นเสมอเมื่อพยายามเรียงต่อกันบนระนาบ
แต่ช่องว่างนี้ไม่ได้เป็นข้อเสียเสมอไป เพราะมันเปิดโอกาสให้เราสามารถพับรูปห้าเหลี่ยมด้านเท่าที่ต่อกันนี้ให้กลายเป็นรูปสามมิติที่เรียกว่าทรง 12 หน้า (dodecahedron) ซึ่งเป็นทรงที่มีความโค้งเป็นบวก (positive curvature) นั่นคือพองออกข้างนอกเหมือนกับลูกบอลได้
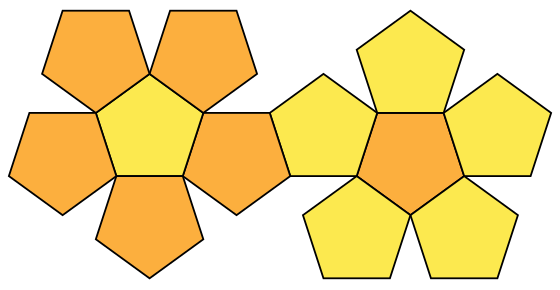
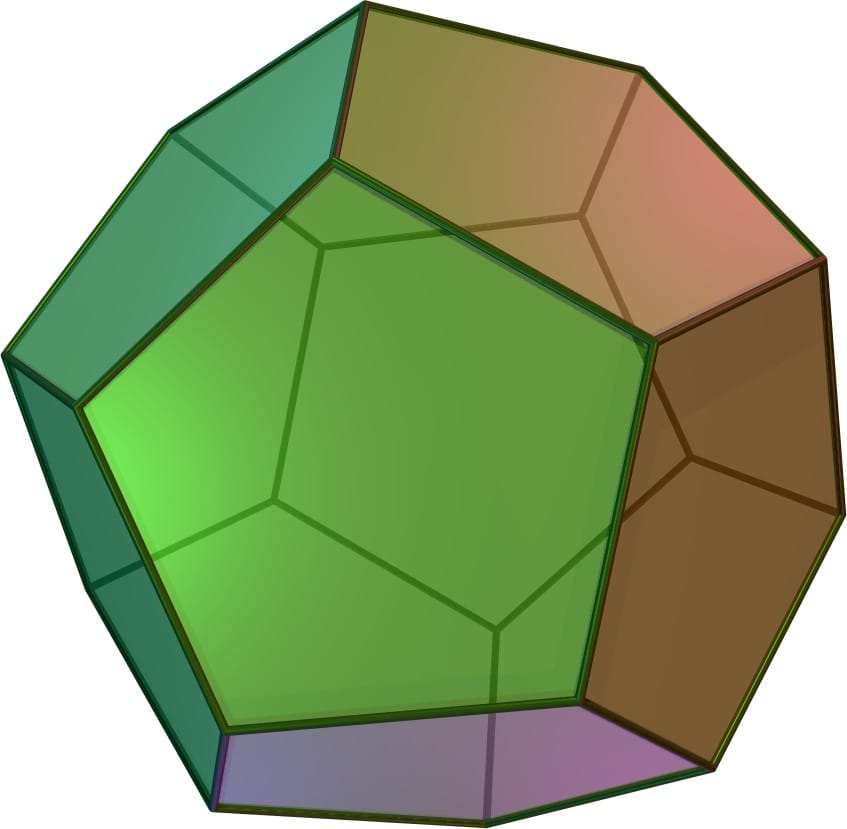
ที่มาภาพ: wikipedia
แนวคิดเรื่องความโค้งนี้ช่วยให้เราเข้าใจได้ว่า ทำไมลูกฟุตบอลแบบคลาสสิกจึงต้องประกอบด้วยรูปห้าเหลี่ยมและหกเหลี่ยมปนกัน เพราะหกเหลี่ยมด้านเท่าสามารถปูระนาบได้เต็มโดยไม่เหลือช่องว่าง จึงไม่สามารถสร้างเป็นรูปทรงโค้งสามมิติได้ ดังนั้นจึงต้องใส่รูปห้าเหลี่ยมปนเข้าไป เพื่อให้ผลรวมของมุมที่จุดยอดน้อยกว่า 360 องศาเล็กน้อย ทำให้สามารถโค้งตัวออกและสร้างเป็นทรงที่มีความโค้งเป็นบวกได้
ในธรรมชาติ นักเคมีพบว่าคาร์บอนสามารถเรียงตัวกันเป็นทรงกลม ซึ่งเป็นทรงเดียวกับฟุตบอลแบบคลาสสิกที่ประกอบขึ้นมาจากรูปห้าเหลี่ยมและหกเหลี่ยมที่เราเห็นกัน

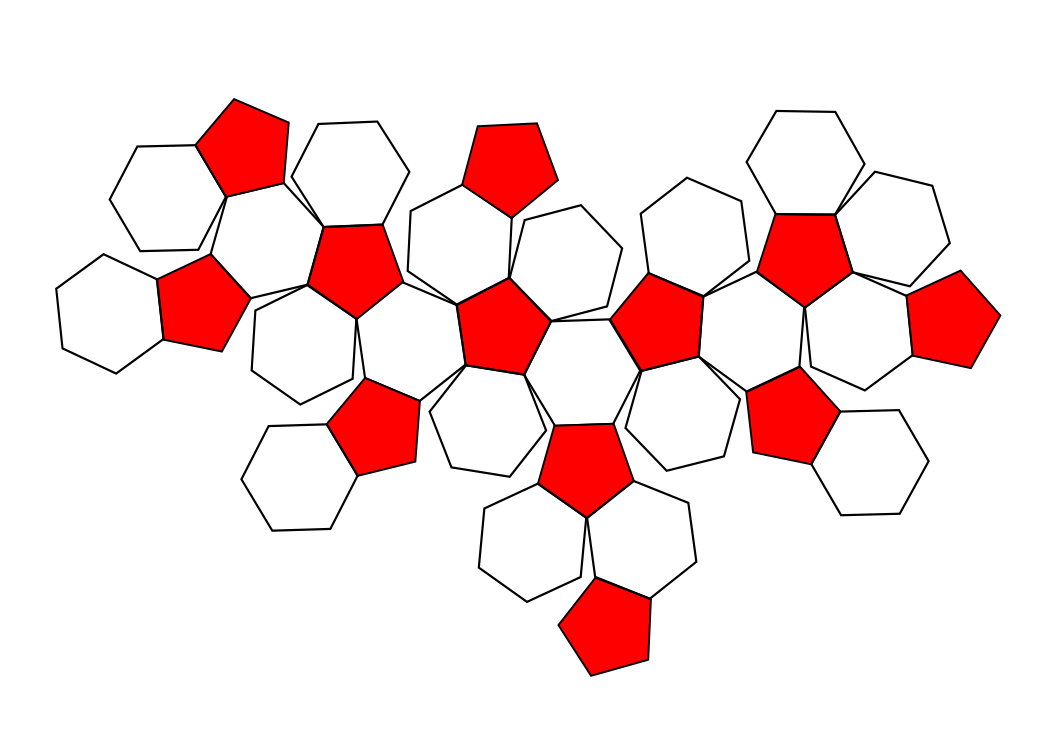
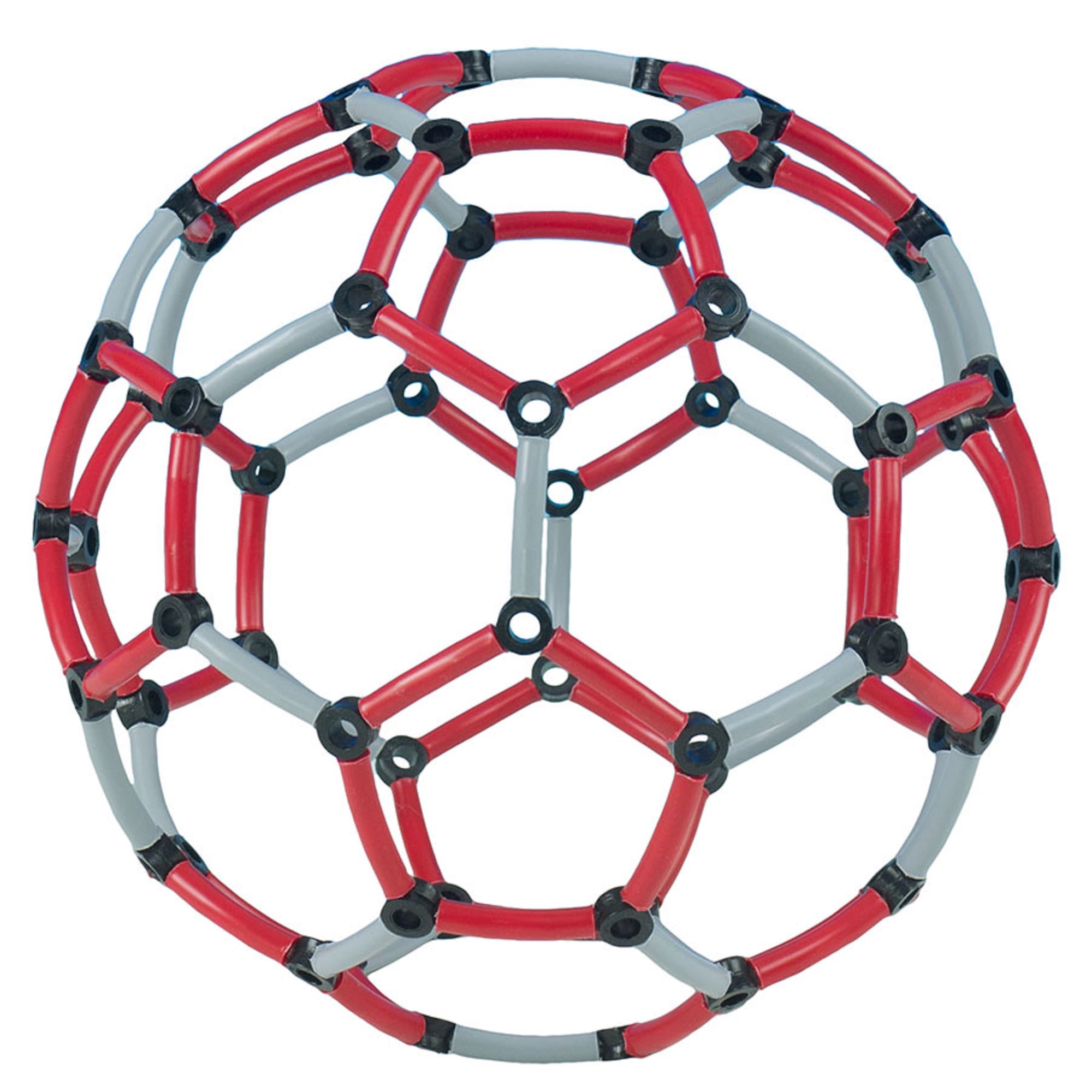
ที่มาภาพ: inannasknitting, hope-education, wikipedia
ในทางกลับกัน ทรงที่ประกอบขึ้นมาจากเจ็ดเหลี่ยมด้านเท่าจะมีความโค้งเป็นลบ (negative curvature) นั่นก็เพราะว่าถ้าเรานำเจ็ดเหลี่ยมสามอันมาต่อกัน มันจะมีมุมประมาณ 128.57 × 3 = 385.71 องศา ซึ่งเกิน 360 ไปนิดนึง หมายความว่ามันมีแนวโน้มจะดันออกจากกันในสามมิติ มันจึงจับตัวกันได้ไม่ดีนัก นั่นทำให้โมเลกุลที่มีโครงสร้างเจ็ดเหลี่ยมปนอยู่ด้วยนั้นพบได้ยากในธรรมชาติ นักวิทยาศาสตร์ต้องสังเคราะห์ขึ้นมาเพื่อให้มีรูปเจ็ดเหลี่ยมโดยเฉพาะ

สิ่งนี้เหมือนจะยิ่งตอกย้ำว่ารูปเจ็ดเหลี่ยมหาได้ยากในธรรมชาติ
แต่ในทางตรงกันข้าม ความโค้งที่เป็นลบของทรงที่ประกอบขึ้นมาจากเจ็ดเหลี่ยมนี่แหละ ที่ทำให้มันเข้ากันได้ดีกับเรขาคณิตที่มีความโค้งเป็นลบ นั่นคือพวก Hyperbolic Geometry ทั้งหลาย เราสามารถพิสูจน์ได้ว่า รูปเจ็ดเหลี่ยมด้านเท่าจะเป็นรูปที่เหมาะสมที่สุดที่จะเอามาใช้ปูพื้นผิวที่มีค่าความโค้งเป็นลบ นั่นคือปูได้เต็มพื้นที่โดยไม่มีช่องว่างเลย

สรุปก็คือ ที่เราไม่ค่อยเห็นรูปเจ็ดเหลี่ยมอยู่รอบตัวนั้นไม่ใช่เพราะมันแปลกประหลาดอะไร มันก็แค่ไม่ค่อยเข้ากับระบบเรขาคณิตแบบยุคลิดที่โลกของเราใช้อยู่เท่านั้นเอง
เพราะถ้ามีผึ้งอาศัยอยู่ในจักรวาลที่มีเรขาคณิตแบบ Hyperbolic ล่ะก็ พวกมันก็คงไม่เลือกสร้างรังเป็นหกเหลี่ยมเหมือนผึ้งในโลกของเรา แต่เลือกใช้เจ็ดเหลี่ยมที่วางต่อกันได้สนิทโดยไม่มีช่องว่างแทน
และเพจคณิตศาสตร์ในจักรวาลนั้นก็อาจจะกำลังเขียนบทความแล้วตั้งชื่อว่า "คุณเคยเห็น 5 เหลี่ยมที่ไหนบ้าง" อยู่ก็ได้
และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ