คุณรู้จักตัวเลขอะไรบ้าง

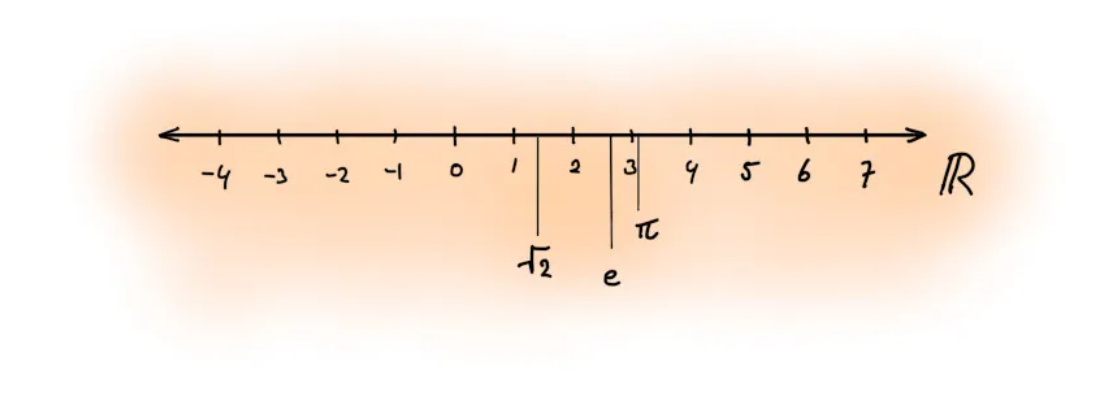
ถ้ามีคนมาถามคุณว่า คุณรู้จักตัวเลขอะไรบ้าง คุณจะตอบว่าอะไร

หลายคนคงเริ่มจากจำนวนนับ 1, 2, 3, 4, … ซึ่งเราได้เรียนรู้มาตั้งแต่อนุบาล หรือเมื่อเราโตขึ้นอีกนิด เราก็เริ่มรู้จักจำนวนเต็มที่รวมถึงเลขศูนย์และจำนวนลบ เช่น -1, -2, -3, ...

ต่อมาเราเรียนรู้ว่ามีตัวเลขที่อยู่ระหว่างจำนวนเต็มพวกนั้น นั่นคือเศษส่วนและทศนิยม ซึ่งช่วยให้เราแบ่งสิ่งของได้ละเอียดขึ้น และเมื่อโตขึ้นอีกหน่อย เมื่อเราเรียนรู้เรื่องเลขยกกำลังและการถอดรูท เราก็พบกับจำนวนที่ดูแปลกใหม่ขึ้น อย่างเช่นสแควร์รูท 2 ที่เรียกว่าจำนวนอตรรกยะ เพราะมันไม่สามารถเขียนเป็นเศษส่วนของจำนวนเต็มได้

คำถามคือคุณรู้จักจำนวนทั้งหมดที่มีในโลกนี้แล้วหรือยัง คุณอาจจะบอกว่าหมดแล้วสิ เพราะคุณครูสอนว่าจำนวนตรรกยะรวมกับจำนวนอตรรยะนั้นได้จำนวนจริง ซึ่งคือทั้งหมดแล้ว ถ้าไม่นับจำนวนเชิงซ้อนน่ะนะ

ก็ถูก ที่คุณพูดมาก็ถูก งั้นผมคงต้องเปลี่ยนคำถามใหม่เป็น คุณรู้จักจำนวนอตกรรยะทั้งหมดที่มีในโลกนี้แล้วหรือยัง

แรกเริ่มเดิมทีเรารู้จักจำนวนอตรรกยะผ่านการถอดราก ไม่ว่าจะเป็นรากที่สอง สาม หรือรากที่ n ใด ๆ หรือพูดให้ครอบคลุมกว่านั้นหน่อย เรารู้จักจำนวนอตรรกยะผ่านการแก้สมการพหุนามที่มีสัมประสิทธิ์เป็นจำนวนตรรกยะ เช่นสแควร์รูท 2 ที่ได้มาจากการแก้สมการ x²=2 หรือรากที่ 3 ของ 5 ที่ได้มาจาการแก้สมการ x³=5

การมองว่าจำนวนตรรกยะคือจำนวนที่ได้จากการแก้สมการพหุนามทำให้เราสามารถสร้างจำนวนอตรรกยะที่แปลกขึ้นได้ อย่างเช่น 

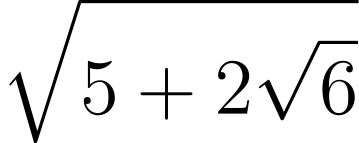
ที่เป็นคำตอบของสมการ (x² - 5)² = 24 ราวกับเราสามารถทำความรู้จักกับจำนวนอตรรกยะทั้งหมดในโลกนี้ได้ ด้วยการแก้สมการพหุนามที่มีสัมประสิทธิ์เป็นจำนวนตรรกยะ

แต่ไม่ใช่ฮะ เพราะในปี 1851 คุณ Joseph Liouville ได้ศึกษาเกี่ยวกับตัวเลขพิเศษตัวหนึ่ง

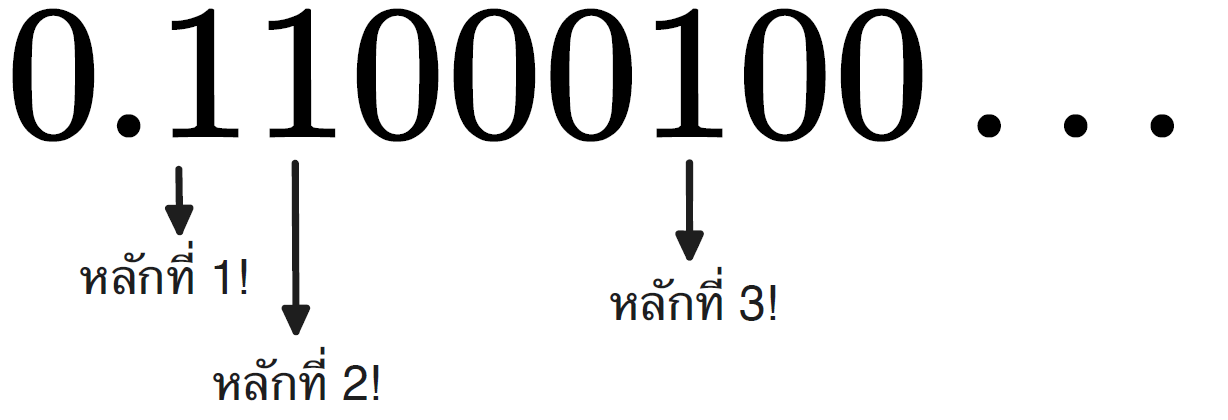
ที่นิยามให้เลขหลังจุดทศนิยมเป็น 0 ทุกหลักเลยยกเว้นหลักที่ 1! 2! 3! … และพบว่าตัวเลขนี้นั้นไม่ได้เป็นคำตอบของสมการพหุนามที่มีสัมประสิทธิ์เป็นจำนวนตรรกยะไหนเลย

เราเรียกจำนวนที่เป็นคำตอบของสมการพหุนามที่มีสัมประสิทธิ์เป็นจำนวนตรรกยะว่า algebraic number หรือจำนวนเชิงพีชคณิต และเรียกจำนวนที่ไม่ได้เป็นคำตอบของสมการพหุนามที่มีสัมประสิทธิ์เป็นจำนวนตรรกยะอะไรเลยว่า transcendental number หรือจำนวนอดิศัย

ตัวเลข 0.1100010… ที่ถูกค้นพบนั้น และถูกเรียกว่า Liouville number ซึ่งถือกันว่าเป็นจำนวนอดิศัยตัวแรก ๆ ที่โลกรู้จัก โดยนอกจาก Liouville number แล้ว นักคณิตศาสตร์ยังค้นพบว่า π และ จำนวนออยเลอร์ e นั้นก็เป็นจำนวนอดิศัย นั่นคือเราไม่มีวันหาพหุนามที่มีสัมประสิทธิ์เป็นจำนวนตรรกยะที่แก้ออกมาแล้วได้ π หรือ e ได้เลย

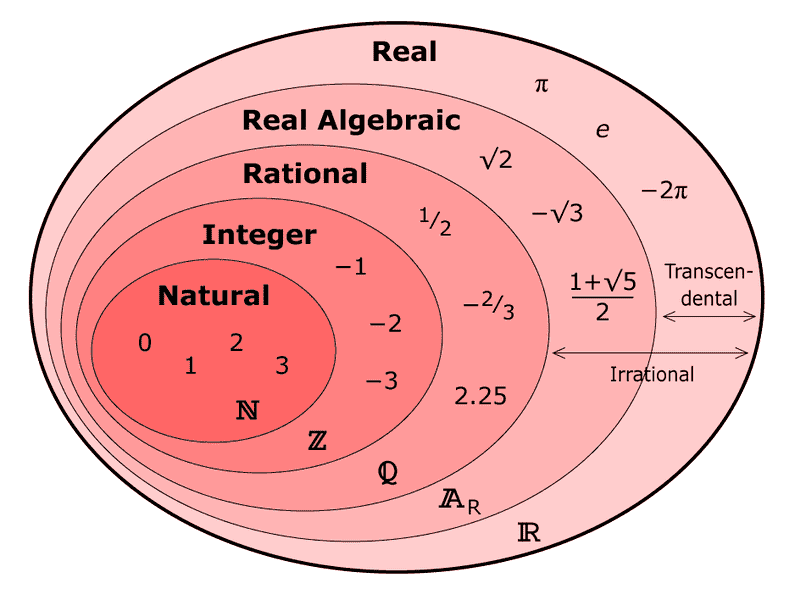
แม้เราจะรู้จักหน้าตาของจำนวนเชิงพีชคณิตเยอะแยะไปหมด แต่นักคณิตศาสตร์กลับสามารถพิสูจน์ได้ว่าจำนวนเชิงพีชคณิตนั้นมีปริมาณน้อยกว่าจำนวนอดิศัยมาก ในแง่ของจำนวนสมาชิกของเซตนั้น จำนวนเชิงพีชคณิตมีปริมาณแค่เท่ากับจำนวนเต็มเท่านั้น นั่นหมายความว่าถ้าเราเอามีดฟันลงไปแบบสุ่ม ๆ บนเส้นจำนวน เราแทบไม่มีโอกาสจะฟันโดนจำนวนเชิงพีชคณิตเลย เพราะการมีอยู่ของมันบนเส้นจำนวนนั้นเบาบางมากเมื่อเทียบกับจำนวนอดิศัย

แต่ในทางตรงกันข้าม ถึงแม้ว่าเราจะรู้ว่าจำนวนจริงแทบทั้งหมดคือจำนวนอดิศัย แต่จำนวนอดิศัยที่เรารู้จักหน้าตาหรือมีชื่อเรียกให้มันจริง ๆ กลับมีอยู่ไม่กี่ตัวเท่านั้น นั่นก็เพราะว่าการพิสูจน์ว่าจำนวน ๆ หนึ่งเป็นจำนวนอดิศัยไหมยากมาก ยากถึงขนาดที่ว่าในปัจจุบันนี้เราก็ยังไม่รู้ด้วยซ้ำว่า e + π, eπ, π^π และ e^eเป็นจำนวนอดิศัยหรือเปล่า

ยิ่งไปกว่านั้น จำนวนอดิศัยที่เราสามารถประมาณค่าได้ด้วยคอมพิวเตอร์กลับมีเพียงหยิบมือเดียว เช่น π และ e ในขณะที่จำนวนอดิศัยส่วนใหญ่นั้น นอกจากจะไม่รู้ว่ามันคืออะไร เราไม่สามารถคำนวณค่าประมาณของมันได้ด้วยซ้ำ นั่นหมายความว่า แม้เราจะรู้ว่าจำนวนอดิศัยนั้นมีอยู่จริงและมีอยู่มากมายขนาดไหน แต่เรากลับแทบไม่เคยได้เห็นหน้าตาของพวกมัน เรารู้เพียงว่ามันซ่อนตัวอยู่ที่ใดสักแห่งบนเส้นจำนวนจริง ที่เราก็ไม่อาจระบุตำแหน่งของมันได้อย่างแน่ชัด

ดังนั้น การดำรงอยู่ของจำนวนอดิศัยจึงเปรียบได้กับอากาศ คือกระจายอยู่ทั่วทุกที่ ยากจะรับรู้ถึงการมีอยู่ได้โดยตรง และมักถูกมองข้าม เพราะมันแทรกซึมอยู่ในช่องว่างระหว่างสิ่งที่เรามองเห็นและให้ความสำคัญ

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง
https://www.quantamagazine.org/recounting-the-history-of-maths-transcendental-numbers-20230627/
https://www.mathsisfun.com/numbers/transcendental-numbers.html
https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/An_Introduction_to_Number_Theory_(Veerman)/01%3A_A_Quick_Tour_of_Number_Theory/1.03%3A_Algebraic_and_Transcendental_Numbers