ถ้าตั้งชื่อบทความนี้ว่า "จริง ๆ แล้วบาสเกตบอลก็ไม่ได้มีอะไรไปมากกว่าการโยนเหรียญ?" ต้องมีทัวร์มาลงแน่ ๆ ดังนั้นผมจะไม่ทำหรอก

ในความรับรู้ของบางคน รวมทั้งผมเองในสมัยเด็ก กีฬากับคณิตศาสตร์ดูเป็นของที่อยู่กันคนละโลกสุด ๆ เพราะกีฬาดูเป็นอะไรที่ว่าด้วยพลังกำลัง ความว่องไวทางกาย และการทำงานเป็นทีม ต่างจากคณิตศาสตร์ที่ดูจะเป็นเรื่องหลักการ เหตุผล และการคำนวณ

งานวิจัยชิ้นที่ผมจะหยิบมาเล่าให้ฟังในบทความนี้มีชื่อว่า Random Walk Picture of Basketball Scoring หรือแปลเป็นไทยว่า ภาพการเดินแบบสุ่มของการทำคะแนนในบาสเกตบอล โดยคุณ Alan Gabel และคุณ Sid Redner เมื่อปี 2011

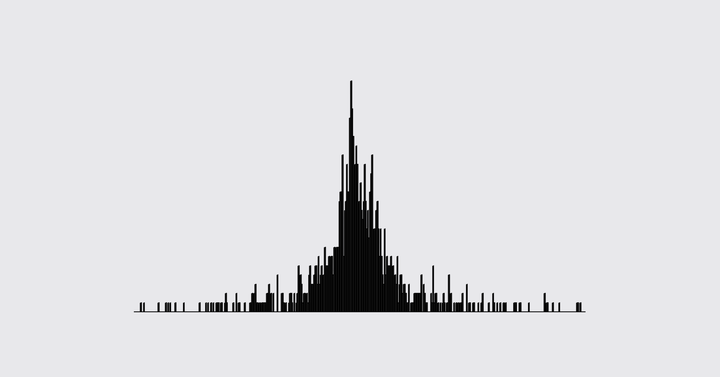
ซึ่งก่อนจะไปพูดถึงตัวงานวิจัย ผมขอปูพื้นฐานก่อนว่า Random Walk หรือการเดินแบบสุ่มนั้นคือคอนเซ็ปต์ทางคณิตศาสตร์ที่พูดถึงค่าที่มีความเปลี่ยนแปลงอย่างสุ่มตามเวลา สมมติว่าชายคนหนึ่งยืนอยู่ที่จุด 0 เขาจะโยนเหรียญหนึ่งครั้ง หากออกหัว เขาจะเดินไปทางข้างหน้าหนึ่งก้าว หากออกก้อย เขาจะเดินถอยหลังหนึ่งก้าว เส้นทางการเดินที่เกิดจากโยนเหรียญและเดินทีละก้าวอย่างนี้ไปเรื่อย ๆ นี่แหละฮะที่เรียกว่า Random Walk

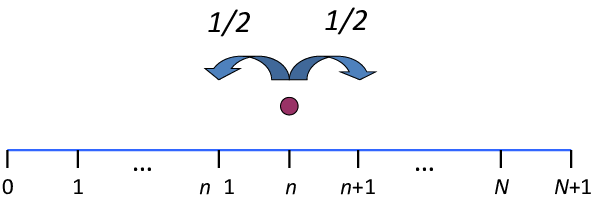
แนวคิดของ Random Walk นี้ฟังดูเรียบง่าย แต่กลับทรงพลังอย่างยิ่งในการนำไปอธิบายปรากฏการณ์ต่าง ๆ ในชีวิตจริง ไม่ว่าจะเป็นการเปลี่ยนแปลงของราคาหุ้น การเคลื่อนที่ของอนุภาคของของเหลว หรือแม้แต่ในเชิงชีววิทยาที่ใช้ศึกษาเส้นทางการหาอาหารของสัตว์

ในงานวิจัยเรื่อง Random Walk Picture of Basketball Scoring นักวิจัยได้นำใช้ข้อมูลแบบ play-by-play จากการแข่งขัน NBA ทั้งหมด 6087 เกมในช่วงฤดูกาล 2006/07 ถึง 2009/10 รวมถึงข้อมูลแพ้ชนะจาก 20 ฤดูกาลที่ผ่านมาวิเคราะห์

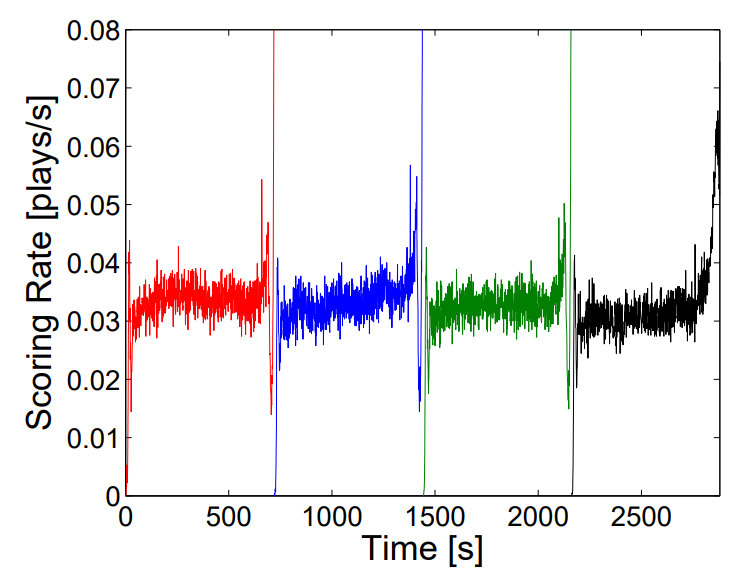
สิ่งแรกที่พวกเขาค้นพบจากการเอาข้อมูลมาวิเคราะห์คือ ระยะเวลาระหว่างการทำแต้มแต่ละครั้งมีลักษณะเป็นการกระจายแบบเอกซ์โพเนนเชียล (Exponential Distribution) ที่มีพารามิเตอร์คงที่แทบจะตลอดทั้งเกม นั่นคือ โอกาสที่การทำแต้มครั้งใหม่จะเกิดขึ้นไม่ได้ขึ้นอยู่กับเวลาในการทำแต้มครั้งก่อน ยกเว้นแค่ในช่วง 10 วินาทีแรก และ 24 วินาทีสุดท้ายของควอเตอร์ ที่อัตราการทำแต้มจะต่ำและสูงเป็นพิเศษตามลำดับ ซึ่งตีความได้ว่า เกมบาสเกตบอลมันไม่ได้มีช่วงเวลาที่ทำแต้มกันอย่างดุเดือดหรือหนักหน่วงเป็นพิเศษอย่างที่แฟนกีฬาเชื่อกัน หากมีก็เป็นแค่ความแปรปรวนที่เกิดจากความผันผวนตามธรรมชาติของกระบวนการสุ่มเท่านั้น

นอกจากนั้น ผู้วิจัยยังพบว่าลำดับการทำแต้มของกีฬาบาสเก็ตบอลยังสามารถอธิบายได้ด้วย random walk คล้ายกับการโยนเหรียญ แต่ไม่ใช่เหรียญธรรมดา ๆ ที่โอกาสออกหัวกับก้อยเท่า ๆ กันที่ 50% แบบที่เราคุ้นเคย

เหรียญที่ว่านี้เป็นเหรียญแบบพิเศษที่มีสมบัติ Anti-Persistence คือ หากรอบที่แล้วมันเพิ่งออกหัวไป รอบถัดไปโอกาสออกก้อยมันจะสูงเป็นพิเศษ ในบริบทของบาสเกตบอลก็คือ หลังจากที่ทีมหนึ่งทำแต้มได้ แต้มถัดไปมีแนวโน้มจะเป็นของอีกทีมมากกว่าจะเป็นทีมเดิมต่อเนื่องกัน อารมณ์ประมาณว่าผลักกันรุกผลัดกับรับ นอกจากนี้โอกาสที่ทีมใดทีมหนึ่งจะทำแต้มได้ยังขึ้นอยู่กับอีกปัจจัยนั่นคือจำนวนแต้มที่ตามอยู่ ผู้วิจัยเรียกสิ่งนี้ว่า Restoring Force

พวกเขาพบว่าทีมที่ตามจะมีแนวโน้มที่จะทำแต้มได้มากตามจำนวนแต้มที่ตามอยู่ สิ่งนี้สะท้อนถึงพฤติกรรมของมนุษย์ที่ทีมที่นำอยู่มักเล่นอย่างผ่อนคลายมากขึ้น ขณะที่ทีมที่ตามหลังพยายามเร่งเกมเพื่อกลับเข้าสู่การแข่งขัน โดยจากการเอาข้อมูลประมวลผลในแบบจำลอง Random Walk ที่สร้างขึ้นพบว่าได้ความน่าจะเป็นที่แต่ละทีมจะเป็นฝ่ายทำแต้มได้คือ

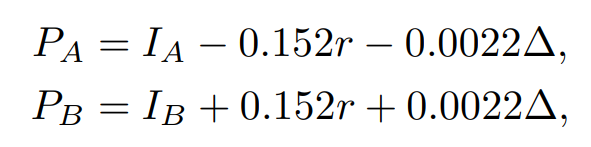
โดยที่ ตัวแปร P คือความน่าจะเป็นที่ทีมนั้นจะทำแต้มได้ ตัวแปร I คือความได้เปรียบจากความเก่งของทีม ตัวแปร r มีค่าเป็น +1 เมื่อแต้มที่แล้วเป็นของทีม A และมีค่าเป็น -1 เมื่อแต้มที่แล้วเป็นของ B และตัวแปร Δ คือผลต่างของแต้มระหว่างสองทีม ซึ่งแปลว่าหากแบบจำลองนี้ถูก เราจะสามารถจำลองแต้มของกีฬาบาสเกตบอลสักเกมได้ด้วยการโยนเหรียญที่กำหนดความน่าจะเป็นที่จะออกหัวและก้อยตามสมการนี้

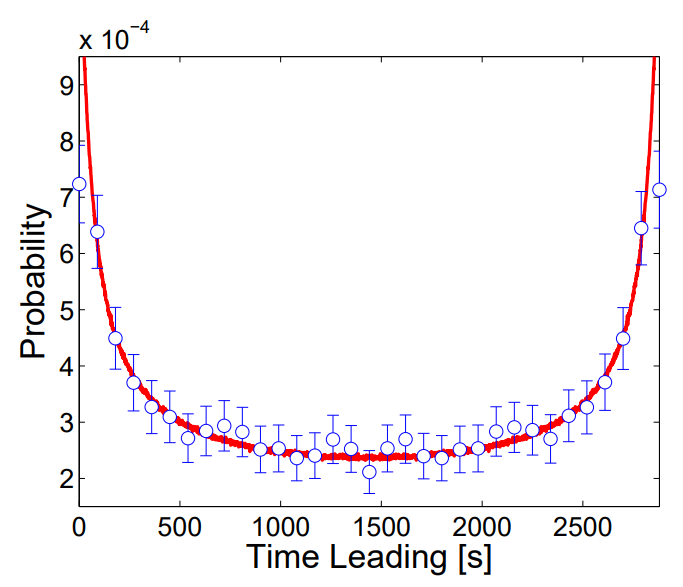
คำถามคือ แบบจำลอง Random Walk นี้อธิบายสิ่งที่เกิดขึ้นในสนามบาสได้ดีแค่ไหน คำตอบก็คือ จากข้อมูล 6087 เกมที่ผู้วิจัยใช้ รวมไปถึงบทความอื่น ๆ ที่ได้ลองเอาข้อมูลการแข่งขันในปีที่ใหม่กว่านั้นมาทดลองด้วย พบว่าแบบจำลองนี้อธิบายแต้มของบาสเกตบอลได้เป็นอย่างดี ค่าทางสถิติที่ได้จากการจำลองนั้นสอดคล้องกับข้อมูลจริง ยกตัวอย่างเช่นการแจกแจงระยะเวลาที่ทีมได้แต้มนำมีลักษณะคล้ายคลึงกับกฎอาร์คไซน์ (Arcsine Law) ของ Random Walk โดยจากกฎนี้ทำให้เราตีความได้ว่า มีโอกาสสูงมากที่ทีมหนึ่งจะมีคะแนนนำตลอดทั้งเกม ในขณะที่ความน่าจะเป็นที่ทั้งสองทีมจะผลัดกันได้คะแนนนำอย่างละเท่า ๆ กันนั้นมีน้อยกว่ามาก แต่สิ่งนี้ก็ไม่ได้หมายความว่าทีมที่ได้คะแนนนำมาตลอดทั้งเกมจะชนะเสมอไป จากที่เราเห็นกันไปแล้วว่าบาสเกตบอลเป็นกีฬาที่มีอัตราการทำแต้มที่สูงมาก ๆ ดังนั้นทีมที่คะแนนตามหลังก็มีโอกาสที่จะพลิกขึ้นมาเป็นเสมอหรือเฉือนชนะทีมที่ได้คะแนนนำมาตลอดทั้งเกมได้เหมือนกัน

อีกข้อสรุปที่ผมอยากเล่าจากงานวิจัยชิ้นนี้คือ จากการทดลองสร้างแบบจำลองด้วยคอมพิวเตอร์เพื่อวิเคราะห์ความสำคัญของแต่ละองค์ประกอบที่ส่งผลต่อความน่าจะเป็น ผลการจำลองแสดงให้เห็นว่าความแตกต่างของความเก่งของทีมไม่ใช่ปัจจัยสำคัญในการกำหนดผลลัพธ์ของเกม เนื่องจากเกมบาสเกตบอลมีความยาวที่จำกัด ทำให้ความแตกต่างที่ว่านั้นถูกกลบไปโดยความผันผวนแบบสุ่ม นั่นจึงทำให้บาสเก็ตบอลเป็นหนึ่งในกีฬาที่คาดเดาผลการแข่งขันได้ยาก

ไม่ใช่แค่งานวิจัยนี้ แต่แบบจำลองเพื่ออธิบายการเปลี่ยนแปลงของแต้มบาสเกตบอลถูกพัฒนาขึ้นมาอย่างต่อเนื่อง มีงานวิจัยหลายชิ้นที่พยายามใช้เครื่องมือทางคณิตศาสตร์ที่ซับซ้อนเพื่อมาอธิบายความผันผวนของแต้มที่เกิดจากลูกบอลสีส้ม ๆ ในสนามรูปสี่เหลี่ยมผืนผ้านี้ เดี๋ยวผมจะแปะลิงก์ไว้ให้เผื่อใครอยากไปตามอ่าน

แน่นอนว่าการได้เข้าใจอะไรบางอย่างอย่างลึกซึ้งเป็นความสนุกสำคัญอย่างหนึ่งของงานด้าน Math Modeling แต่ถ้ามองไปให้ไกลกว่านั้น การทำความเข้าใจคณิตศาสตร์ที่อยู่เบื้องหลังสิ่งต่าง ๆ ยังเป็นประตูไปสู่อะไรอีกมากมาย ทุกวันนี้นักสถิติและนักคณิตศาสตร์มีบทบาทสำคัญในการช่วยโค้ชและนักกีฬาเข้าใจประสิทธิภาพของทีมและตัวผู้เล่น ไม่เพียงเท่านั้น ความรู้ทางคณิตศาสตร์ยังถูกนำมาใช้เพื่อวางกลยุทธ์การแข่งขันแบบเรียลไทม์ผ่านการวิเคราะห์ข้อมูลเฉพาะหน้า การตัดสินใจว่าจะเปลี่ยนตัวผู้เล่นเมื่อไร จะบุกหรือรับในสถานการณ์ไหน ก็ล้วนต้องอาศัยหลักการคณิตศาสตร์และความน่าจะเป็นเข้ามาประกอบทั้งสิ้น จนเราอาจพูดได้ว่า คณิตศาสตร์ไม่ใช่แค่เครื่องมือในการเข้าใจเกม แต่ยังเป็นตัวเปลี่ยนเกมที่สามารถสร้างความได้เปรียบในการแข่งขันได้อย่างมหาศาล

พร้อมยังฮะ ผมจะขายของแล้วนะ

และสำหรับใครที่อยากรู้จักกับวิชา Math Modeling นี้ให้มากขึ้น ผมอยากชวนมาเรียน ‘Math Modeling 1.0’ กับผม พรรษ วติวุฒิพงศ์ นักคณิตศาสตร์ และเจ้าของเพจคณิตศาสตร์อย่างที่ควรจะเป็น รู้จักกับเครื่องมือทางคณิตศาสตร์เพื่อทำความเข้าใจระบบ กลไก และกฎระเบียบของธรรมชาติด้วยเครื่องมือทางคณิตศาสตร์ได้ที่

https://unfoldthedice.onlinecoursehost.com/courses

พิเศษ! Promotion รับปีใหม่
เพียงใส่โค้ด UFD2025 เมื่อซื้อคอร์สใดก็ได้
จะได้รับส่วนลด 25% ไปเลย
ตั้งแต่วันนี้ - 31 ธันวาคม 2567 เท่านั้น

สอบถามรายละเอียดเพิ่มเติมได้ทาง inbox เพจคณิตศาสตร์อย่างที่ควรจะเป็นเลยนะฮะ

เอกสารอ้างอิง
• Random Walk Picture of Basketball Scoring https://arxiv.org/pdf/1109.2825v1
• Is Basketball a Random Walk? https://hasithv.github.io/posts/projects/24-08-17-basketballrandomwalk/
• Modeling basketball play-by-play data https://linkinghub.elsevier.com/retrieve/pii/S095741741500617X
• A functional data approach to model score difference process in professional basketball games https://www.tandfonline.com/doi/full/10.1080/02664763.2016.1268106
• A gamma process based in-play prediction model for National Basketball Association games
https://linkinghub.elsevier.com/retrieve/pii/S0377221719309233