เราเทียบสัมประสิทธิ์ได้เสมอหรือเปล่า

การเทียบสัมประสิทธิ์เป็นสิ่งที่เราทำกันมาตั้งแต่เด็ก ๆ เช่น ในสมการพหุนาม

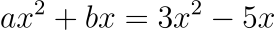
เราสามารถเทียบสัมประสิทธิ์ของแต่ละพจน์เพื่อสรุปว่า a = 3 และ b = -5 ได้ หรือแม้แต่สมการที่ซับซ้อนขึ้นอย่าง

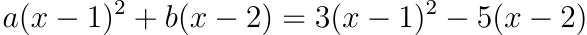
เราก็สามารถใช้วิธีเทียบสัมประสิทธิ์ของแต่ละพจน์เพื่อสรุปว่า a = 3 และ b = -5 ได้เช่นกัน ความจริงแล้วในกระบวนการ Partial Fraction หรือแก้สมการเชิงอนุพันธ์ด้วย Method of Undetermined Coefficients เราก็ใช้การเทียบสัมประสิทธิ์เพื่อหาค่าคงที่ที่เราไม่ทราบ

ซึ่งพอเห็นแบบนี้บ่อยเข้า เราอาจจะเผลอคิดไปว่าเราสามารถเทียบสัมประสิทธิ์ได้เสมอ ซึ่งในความเป็นจริงแล้วไม่เป็นอย่างนั้น เช่นถ้าเรามีสมการ

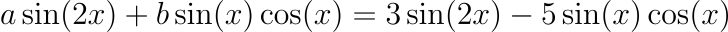
เราจะเทียบสัมประสิทธิ์เพื่อหาค่า a กับ b โดยตรงไม่ได้ เพราะจากความรู้เรื่องตรีโกณมิติเราสามารถแปลงร่าง sin(2x) ให้เป็น 2sin(x)cos(x) ได้ และทำให้สมการที่เราจะแก้กลายเป็น

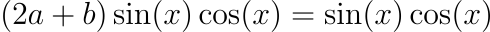
ซึ่งทำให้เราสรุปค่าของ a กับ b ตรง ๆ แบบที่ทำในข้อก่อน ๆ ไม่ได้ หรืออย่างสมการ

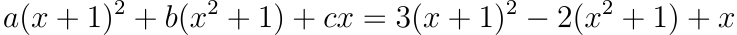
ที่เหมือนจะหาค่า a b และ c ด้วยการเทียบสัมประสิทธิ์ได้ ทั้งที่จริงแล้วก็ไม่ เพราะเราพบว่าก้อนแรกซึ่งคือ (x+1)² นั้นสามารถเขียนเป็น (x²+1) + 2(x) ซึ่งคือ ผลบวกของก้อนที่เหลือคูณกับตัวเลข ได้

การที่ใครสักก้อนสามารถเขียนในรูปของ ผลบวกของก้อนที่เหลือคูณกับตัวเลข ได้นั้นเรียกว่าก้อนเหล่านั้นมันมีสมบัติไม่อิสระเชิงเส้น และเงื่อนไขของฟังก์ชันที่จะสามารถใช้วิธีเทียบสัมประสิทธิ์เพื่อหาค่าคงที่ได้นั้นจะต้องมีสมบัติอิสระเชิงเส้นกัน นั่นคือไม่มีฟังก์ชันไหนที่สามารถเขียนในรูปของผลบวกของฟังก์ชันที่เหลือคูณกับตัวเลขได้เลย

เขียนให้เป็นคณิตศาสตร์หน่อย ฟังก์ชัน f₁(x), f₂(x), ..., f_n(x) จะมีอิสระเชิงเส้นกันก็ต่อเมื่อสมการ c₁f₁(x) + c₂f₂(x) + ... + f_n(x) = 0 มีเพียงคำตอบเดียวที่ c₁ = c₂ = ... = c_n = 0 เท่านั้น

ในทางปฏิบัติ วิธีหนึ่งที่สามารถใช้ตรวจสอบว่าเซตของฟังก์ชันเป็นอิสระเชิงเส้นหรือไม่ คือการใช้ Wronskian Determinant ซึ่งนิยามโดย

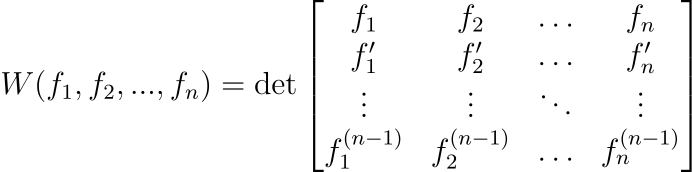
ซึ่งถ้าค่า W ที่ได้นั้นไม่เท่ากับศูนย์สำหรับทุกค่า x ในช่วงที่เราสนใจ แสดงว่าฟังก์ชันเหล่านั้นอิสระเชิงเส้นกัน แต่สำหรับฟังก์ชันที่มีสมบัติ analytic หาก W เป็นศูนย์แค่บางค่า x เราจะสรุปได้เลยว่าฟังก์ชันเหล่านั้นไม่อิสระต่อกัน

เช่นเราพบว่า

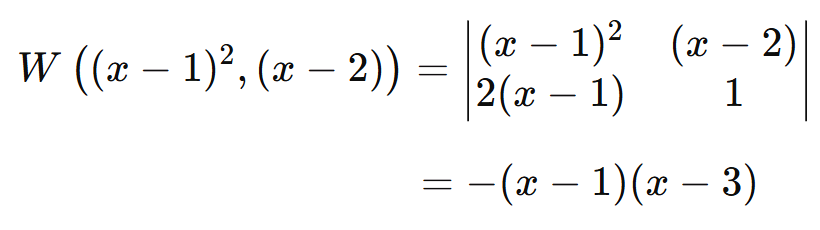
ซึ่งไม่เท่ากับ 0 บนช่วง x ที่ไม่มี 1 กับ 3 แสดงว่าเราสามารถเทียบสัมประสิทธิในช่วงพวกนั้นได้ ในขณะที่

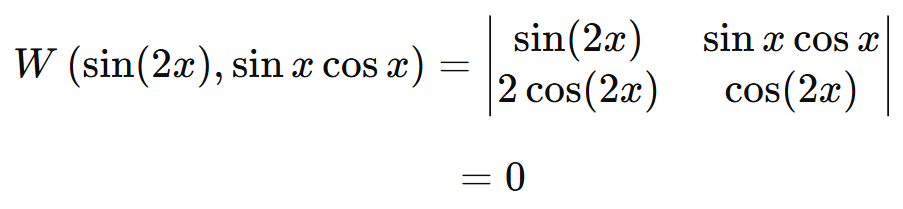
และ

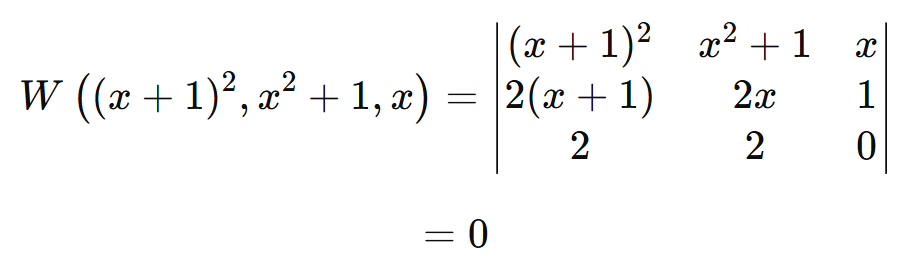
นั้นเท่ากับศูนย์เสมอไม่ว่า x จะเป็นเท่าไร แสดงว่าไม่มีช่วงไหนเลยที่เราสามารถเทียบสัมประสิทธิ์ได้

นั่นจึงเป็นเหตุให้ทุกครั้งที่เราจะเทียบสัมประสิทธิ์ไม่ว่าจะเพื่อทำ Partial Fraction แก้สมการเชิงอนุพันธ์ด้วย Method of Undetermined Coefficients หรือเพื่ออะไรก็ตาม การตรวจสอบให้แน่ใจว่าแต่ละฟังก์ชันนั้นอิสระเชิงเส้นกันด้วย Wronskian Determinant จึงสำคัญมาก

และนิทานเรื่องนี้ก็สอนให้เรารู้ว่า ของหลาย ๆ อย่างที่เราทำกันมาตั้งแต่เด็ก ๆ นั้นมันไม่ได้ทำได้ตลอดเวลาเสมอไป ตอนสอนครูเขาก็อาจจะแค่แต่งโจทย์ให้มันอยู่ในกรณีที่ทำได้เท่านั้นเอง

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง
https://library.fiveable.me/key-terms/calc-ii/method-of-equating-coefficients
https://tutorial.math.lamar.edu/classes/de/undeterminedcoefficients.aspx
https://math.libretexts.org/Bookshelves/Analysis/Supplemental_Modules_(Analysis)/Ordinary_Differential_Equations/3%3A_Second_Order_Linear_Differential_Equations/3.6%3A_Linear_Independence_and_the_Wronskian
https://math.mit.edu/classes/18.03/sup/sup19.pdf