รูปเรขาคณิตสุดประหลาด ที่ลากเส้นตามขอบยังไงก็ไม่รอบ

เรื่องมันมีอยู่ว่า ผมเพิ่งได้ไปอ่านโพสท์นึงที่พูดถึงเกมแกะขนมน้ำตาลจากซีรีส์เรื่อง Squid Game ที่ในซีซั่นนี้นั้นระดับความยากของมันซับซ้อนกว่าของซีซั่นแรกมาก ซีซั่นแรกอันยากสุดเป็นรูปร่ม พอมาซีซั่นนี้ที่พระเอกจับไต๋ได้ ทีมงานเลยตลบหลังกลับด้วยการให้แกะรูปสามเหลี่ยมซ้อนกันที่แสนจะซับซ้อน จนคนดูเอามาแซ็วกันว่า ซีซั่นสองยังยากขนาดนี้ ซีซั่นสามจะต้องยากขนาดไหน

ผมก็เลยนึกไปถึงรูปเรขาคณิตอันหนึ่งที่มีสมบัติทางคณิตศาสตร์อันแสนจะประหลาด ที่เรียกว่า Koch Snowflake หรือว่า เกล็ดหิมะของโคช ซึ่งเป็นผลงานการคิดค้นของนักคณิตศาสตร์ชาวสวีเดนที่ชื่อว่าคุณ Helge von Koch ในปี 1904

ไอเดียของมันง่ายมากฮะ ใครอ่านแล้วตามไม่ทันลองดูรูปข้างล่างประกอบไปด้วยได้

เริ่มต้นเราสร้างรูปสามเหลี่ยมด้านเท่าขึ้นมารูปหนึ่งฮะ (รูปซ้ายบน) จากนั้น แบ่งด้านทั้งสามออกเป็นสามส่วนที่ยาวเท่า ๆ กัน แล้วสร้างยอดด้วยการวาดสามเหลี่ยมด้านเท่าเล็ก ๆ บนส่วนกลางของแต่ละส่วน (รูปขวาบน) มันก็จะออกมาเป็นรูปคล้าย ๆ ดาว 6 แฉกที่ทุกด้านยาวเท่ากัน

จากนั้นเราก็ทำแบบเดิมเลย นั่นก็คือแบ่งแต่ละด้านออกเป็นสามส่วน แล้วก็สร้างยอดด้วยการวาดสามเหลี่ยมด้านเท่าเล็ก ๆ บนส่วนกลางของแต่ละส่วน มันก็จะกลายเป็นรูปซ้ายล่าง และรูปขวาล่างตามลำดับฮะ

แต่เราจะไม่หยุดอยู่แค่นั้น เราจะทำกระบวนการนี้ซ้ำไปเรื่อย ๆ ไปเป็นอนันต์ครั้งเลยฮะ ผลที่ได้ก็จะเป็นรูปที่ออกมาคล้ายกับรูปเกล็ดหิมะ ที่ถ้าเราซูมเข้าไปดูใกล้ ๆ ก็จะพบว่ามันจะมีหน้าตาเหมือนเดิมไปเรื่อย ๆ ไม่ว่าจะซูมเข้าไปลึกแค่ไหน

รูปทรงเรขาคณิตที่มีโครงสร้างซ้ำซ้อนและแสดงความเหมือนเดิมในทุกระดับของการซูมเข้าไปแบบนี้นั้นเรียกว่า fractal ฮะ โดย Koch Snowflake นั้นก็เป็น fractal ตัวหนึ่ง ซึ่งพอพูดถึง fractal นั้น ความจริงแล้วก็มีรายละเอียดทางคณิตศาสตร์ที่น่าสนใจอีกเยอะแยะเลย แต่นั่นไม่ใช่ประเด็นที่ผมจะเล่าในบทความนี้ ดังนั้นจึงขอติดเอาไว้ก่อน เพราะสิ่งที่ผมจะเล่าเกี่ยวกับเจ้า Koch Snowflake นั้นคือพื้นที่และเส้นรอบรูปของมันต่างหาก

เริ่มจากพื้นที่ก่อน ถ้าเรากำหนดให้แต่ละด้านของสามเหลี่ยมด้านเท่าตอนเริ่มต้นมีค่าเท่ากับ 1 หน่วย การหาพื้นที่ของ Koch Snowflake หลังจากการทำซ้ำไป n ครั้งนั้นสามารถทำได้จากการเอาพื้นที่สามเหลี่ยมด้านเท่าแต่ละชิ้นที่สร้างขึ้นมาบวกกัน ซึ่งผมคำนวณมาให้เลยว่าได้

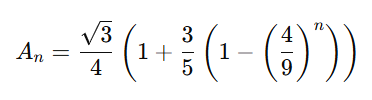
อันนี้คือพื้นที่ของมันหลังจากการทำซ้ำไป n ครั้ง ดังนั้นถ้าเราอยากหาพื้นที่ของ Koch Snowflake แบบที่ทำซ้ำไปจนถึงอนันต์ครั้ง เราก็แค่ take limit ให้ n เข้าสู่อนันต์ ซึ่งจากความรู้เรื่องลำดับเรขาคณิตจะได้ว่า

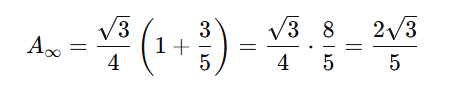
ส่วนเส้นรอบรูปนั้นก็ทำด้วยวิธีเดียวกัน คือเริ่มต้นจากการหาเส้นรอบรูปของ Koch Snowflake หลังจากการทำซ้ำไป n ครั้งก่อน ซึ่งได้

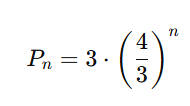
ซึ่งเป็นลำดับที่ลู่ออก ประหลาดไหมฮะ

ถ้าใครยังตามไม่ทันว่าการที่เส้นรอบรูปของ Koch Snowflake หลังจากการทำซ้ำไป n ครั้งนั้นออกมาเป็นลำดับที่ลู่ออกนั้นประหลาดยังไง การที่ลำดับนั้นลู่ออกแปลว่าเส้นรอบรูปของเจ้า Koch Snowflake นี้มีค่าเป็นอนันต์น่ะสิฮะ

คือลองนึกตามผมนะ ถ้าผมมีวงกลมอยู่รูปหนึ่ง แล้วผมขยายรัศมีของมันไปจนเป็นอนันต์ ผมก็จะได้วงกลมขนาดใหญ่มาก ๆ ที่มีพื้นที่เป็นอนันต์ และเส้นรอบวงเป็นอนันต์ด้วย ถูกไหมฮะ ซึ่งก็ฟังดูปกติดี รูปที่มีขนาดใหญ่มาก ๆ ก็ควรจะมีพื้นที่และเส้นรอบรูปเป็นอนันต์

แต่เจ้า Koch Snowflake นี้นั้นมีพื้นที่จำกัด แต่กลับมีเส้นรอบรูปเป็นอนันต์เฉยเลย พูดให้เห็นภาพกว่านั้นก็คือ ถ้าผมต้องการลงสีรูป Koch Snowflake ให้เต็มพื้นที่ ผมระบายไปสักพักเดี๋ยวก็เต็มรูปแล้ว แต่ถ้าผมต้องการตัดเส้น นั่นคือการลากปากกาไปตามเส้นรอบรูป ผมจะต้องใช้เวลาเป็นอนันต์เลยกว่าจะตัดเส้นรูปนี้เสร็จ

ดังนั้นถ้า Squid Game ต้องมีซีซั่นสามแล้วอยากได้เกมแกะขนมน้ำตาลเวอร์ชั่นยากระดับ pro max ถึงขนาดที่ผู้เล่นไม่มีทางแกะได้เลย ผมแนะนำว่าให้ทำเป็นรูป Koch Snowflake เลยฮะ แต่เอ๊ะ พอมาคิดอีกที ถ้าเส้นรอบรูปของ Koch Snowflake นั้นเป็นอนันต์จนทำให้ผู้เล่นไม่สามารถแกะได้ แล้วทีมงานจะสร้างรูปของมันขึ้นมาบนชิ้นขนมได้ยังไงหว่า

Koch Snowflake เป็นหนึ่งตัวอย่างที่แสดงให้เห็นว่าสามัญสำนึกของมนุษย์มักจะไม่เพียงพอเมื่อต้องรับมือกับโครงสร้างในระดับอนันต์ นั่นจึงอาจจะเป็นเหตุผลที่วิชาแคลคูลัสนั้นเป็นไม้เบื่อไม้เมากับผู้ศึกษามันมาทุกยุคทุกสมัย เพราะแคลคูลัสนั้นเป็นศาสตร์ที่วอแวอยู่กับของที่เยอะเป็นอนันต์ ใกล้กันเป็นอนันต์ หรือแบ่งถี่เป็นอนันต์ ซึ่งแสนจะเป็นอะไรที่ขัดแย้งกับสามัญสำนึกของคนเราอย่างยิ่ง

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง
https://mathworld.wolfram.com/KochSnowflake.html
https://fractalfoundation.org/resources/what-are-fractals/