เราจะหาจำนวนเฉพาะที่ใหญ่ขึ้นเรื่อย ๆ ไปทำไม

เมื่อวันที่ 21 ตุลาที่ผ่านมา มีข่าวการค้นพบจำนวนเฉพาะที่ใหญ่ที่สุดในโลกตัวใหม่ นั่นคือ
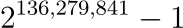
ซึ่งถ้าเอามาเขียนเป็นเลขฐานสิบจะมีความยาวถึง 41,024,320 หลัก โดยคุณ Luke Durant และทีม Great Internet Mersenne Prime Search (GIMPS)
สำหรับคนที่มีพื้นฐานเรื่องนี้ จำนวนเฉพาะคือจำนวนนับที่มากกว่า 1 ที่มีตัวประกอบแค่สองตัว คือตัวมันเองและ 1 อย่างเช่น 12 นั้นไม่ใช่จำนวนเฉพาะ เพราะมันมี 1 2 3 4 6 และ 12 เป็นตัวประกอบ ในขณะที่ 13 นั้นเป็นจำนวนเฉพาะ เพราะตัวประกอบของมันมีแค่ 1 และ 13 เท่านั้น
จำนวนเฉพาะถูกเรียกว่าเป็น อะตอมแห่งระบบจำนวน เนื่องจากบทบาทพื้นฐานของมันในการสร้างจำนวนเต็มทั้งหมด ซึ่งคล้ายกับการที่อะตอมเป็นหน่วยย่อยพื้นฐานของสสารในวิชาเคมี
จำนวนเฉพาะที่ใหญ่ที่สุดก่อนหน้านี้ที่เรารู้จักถูกค้นพบเมื่อปี 2018 มีค่าเท่ากับ
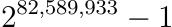
ซึ่งเขียนออกมาได้เป็นตัวเลข 24,862,048 หลัก คือสั้นกว่าตัวล่าสุดที่ค้นพบถึงเกือบครึ่งนึง คำถามที่น่าสนใจคือ แล้วการค้นพบจำนวนเฉพาะที่ใหญ่ขึ้นนั้นมันสำคัญยังไง
เพราะนักคณิตศาสตร์ไม่รู้ว่ามีจำนวนเฉพาะอยู่มากมายแค่ไหน การค้นพบจำนวนเฉพาะใหม่ ๆ มันเลยสำคัญอย่างนั้นหรอ?
ผิดฮะ ไม่ใช่เลย นักคณิตศาสตร์รู้มาตั้งแต่ 2300 กว่าปีแล้วว่าจำนวนเฉพาะนั้นมีอยู่มากมายนับไม่ถ้วน ยุคลิดเคยพิสูจน์ข้อเท็จจริงนี้ไว้ด้วยบทพิสูจน์ที่แสนสวยงาม เขาบอกว่าถ้าในโลกนี้มีจำนวนเฉพาะอยู่อย่างจำกัด ถ้าเราให้ N แทนจำนวนเฉพาะตัวที่มากที่สุด เราจะได้ว่า (2⋅3⋅5⋅...⋅N)+1 นั้นจะเป็นจำนวนเฉพาะเช่นกัน เพราะมันหารด้วยจำนวนเฉพาะที่น้อยกว่ามันตัวไหนไม่ได้เลย ดังนั้นแปลว่าเราจะหาจำนวนเฉพาะที่ใหญ่กว่า N ได้เสมอ นั่นคือมีจำนวนเฉพาะอยู่อนันต์ตัวนั่นเอง
แต่บทพิสูจน์ของยูคลิดบอกเราได้แค่ว่า มีจำนวนเฉพาะอยู่มากมายนับไม่ถ้วน แต่ไม่ได้บอกว่าเราจะหาจำนวนเฉพาะตัวต่อไปได้ยังไง
คุณ Marin Mersenne นักคณิตศาสตร์ชาวฝรั่งเศสศึกษาเกี่ยวกับจำนวนในรูป (2^p)-1 เมื่อ p เป็นจำนวนเฉพาะ เขาพบว่า 2 เป็นจำนวนเฉพาะ และ (2^2)-1 ซึ่งเท่ากับ 3 ก็เป็นจำนวนเฉพาะด้วย หรือ 13 เป็นจำนวนเฉพาะ และ (2^13)-1 ซึ่งเท่ากับ 8191 ก็เป็นจำนวนเฉพาะด้วย
ราวกับจะสรุปได้ว่า (2^p)-1 จะเป็นจำนวนเฉพาะเสมอถ้า p เป็นจำนวนเฉพาะ ซึ่งถ้าสูตรนี้จริงมันจะทำให้เราพอจะหาแพทเทิ่นของจำนวนเฉพาะได้ แต่ข่าวร้ายคือสูตรนี้ไม่ได้จริงเสมอไป อย่างเช่น 11 ที่จำนวนเฉพาะ แต่ (2^11)-1 ซึ่งเท่ากับ 2047 นั้นไม่เป็นจำนวนเฉพาะ แสดงว่า (2^p)-1 อาจจะเป็นจำนวนเฉพาะหรือไม่เป็นก็ได้ โดยเราจะเรียกจำนวนเฉพาะที่อยู่ในรูปของ (2^p)-1 นี้ว่า จำนวนเฉพาะ Mersenne ตามชื่อของคุณ Marin Mersenne

ไม่ใช่แค่คุณ Mersenne มีนักคณิตศาสตร์จำนวนมากพยายามจะหาแพทเทิ่นของจำนวนเฉพาะ แต่ก็คว้าน้ำเหลวกันไปอย่างถ้วนหน้า จนถึงปัจจุบันก็ยังไม่มีใครที่หาสูตรสำหรับหาจำนวนเฉพาะออกมาได้ สิ่งที่เราพอทำได้จึงคือการไล่เช็คเลขไปทีละตัว ว่าตัวนี้เป็นจำนวนเฉพาะหรือเปล่า
เช่นถ้าเราอยากรู้ว่า 111 เป็นจำนวนเฉพาะไหม เราก็แค่เอาจำนวนเฉพาะทุกตัวที่เล็กกว่า 111 ไปไล่หารแล้วดูว่าหารลงตัวไหม เราพบว่า 3 นั้นหาร 111 ลงตัว แสดงว่า 111 ไม่ใช่จำนวนเฉพาะ
การตรวจสอบว่าจำนวนที่สนใจเป็นจำนวนเฉพาะหรือไม่ด้วยการไล่หารไปเรื่อย ๆ นั้นฟังดูง่ายมากเมื่อเราทำกับเลขน้อย ๆ แต่ลองนึกว่าถ้าเราเอาไปทำกับตัวเลขที่ยาวเป็นหลายสิบล้านหลัก การโกยเอากวาดจำนวนเฉพาะทั้งหมดที่น้อยกว่ามันมาไล่หารมันไปเรื่อย ๆ ทีละตัวนั้นเป็นงานสุดหินที่ต้องการการประมวลผลทางคอมพิวเตอร์ที่ทรงพลังมาก ๆ
ทีม Great Internet Mersenne Prime Search (GIMPS) ก่อตั้งขึ้นในปี 1996 โดยมีเป้าหมายเพื่อค้นหาจำนวนเฉพาะ Mersenne ที่มีขนาดใหญ่ขึ้นเรื่อย ๆ พวกเขาค้นพบจำนวนเฉพาะ Mersenne ขนาดใหญ่ยักษ์มาแล้วถึง 18 ตัว ก่อนจะมาถึงตัวล่าสุดที่เพิ่งออกข่าวไป

ก่อนหน้านี้พวกเขาต้องใช้คอมพิวเตอร์ที่มีกำลังการประมวลผลสูงมาก ๆ ในการค้นหาจำนวนเฉพาะขนาดใหญ่ แต่เมื่อศักยภาพ GPU มีมากขึ้น พวกเขาจึงสร้างระบบเพื่อรันซอฟต์แวร์ GIMPS บนเซิร์ฟเวอร์ GPU หลายตัวทั่วโลก
คุณ Luke Durant เพิ่งเข้าร่วมทีมค้นหาจำนวนเฉพาะของ GIMPS เป็นเวลาไม่ถึงปี เขาเชื่อว่า GPU ที่ใช้ในการเล่นเกมและการคำนวณด้าน AI จะสามารถเอามาใช้ช่วยหาจำนวนเฉพาะได้ เขาจึงสร้างเครือข่าย GPU หลายพันเครื่องในศูนย์ข้อมูล 24 แห่งใน 17 ประเทศ โดยหวังว่าจะทำทำให้ขอบเขตการค้นหาขยายตัวได้มากกว่าเดิม และก็เป็นอย่างนั้นจริง ๆ
คนที่พอมีความรู้เรื่องการเข้ารหัสด้วยจำนวนเฉพาะขนาดใหญ่มากบ้าง อาจจะเข้าใจไปว่าการค้นพบจำนวนเฉพาะขนาดใหญ่ยักษ์เหล่านี้จะช่วยทำให้พัฒนาการเข้ารหัสลับของมนุษย์ แต่ไม่ใช่ เพราะถึงแม้ว่าในการเข้ารหัสจะต้องใช้จำนวนเฉพาะขนาดใหญ่ แต่ต้องไม่ใหญ่ขนาดนี้ จำนวนเฉพาะที่พวกเขาค้นพบกันอยู่นี้นั้นใหญ่กว่าที่เราใช้เพื่อเข้ารหัสกันไปมาก
ดังนั้นถ้าพูดถึง ณ วินาทีนี้ การค้นพบจำนวนเฉพาะขนาดใหญ่พวกนี้ก็ต้องถือว่าไม่ได้มีประโยชน์อะไรโดยตรงกับเรา ทั้งในทางคณิตศาสตร์ และในทางการประยุกต์ใช้ แต่การที่สิ่งที่ค้นพบมันไม่มีประโยชน์ ไม่ได้แปลว่ากระบวนการที่ใช้ค้นพบมันนั้นไม่มีประโยชน์นี่นา ทุกวันนี้การค้นหาจำนวนเฉพาะถูกใช้เป็นเหมือนโจทย์ที่ท้าทาย รอคอยให้นักวิจัยด้านอัลกอริธึมและเทคโนโลยีการประมวลผลตบเท้ากันเข้ามาท้าประลอง และขยายขีดจำกัดการประมวลผลของคอมพิวเตอร์ออกไป ดูจากการค้นพบจำนวนเฉพาะขนาดใหญ่ที่เห็นตัวล่าสุดก็ได้ มันแสดงให้เห็นถึงพลังของการประมวลผลแบบใหม่ ๆ ที่เปลี่ยนปัญหาที่เราเคยแก้ไม่ได้ ให้กลายเป็นปัญหาที่แก้ได้ขึ้นมา
และเช่นเดิม ใครที่อยากช่วยสนับสนุนเพจเว็บไซต์ของเราให้ผลิตคอนเทนต์คณิตศาสตร์ที่ไม่น่าจะมีคนยอมจ้างให้ไปเขียนลงที่ไหนอย่างนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ
แหล่งอ้างอิง
https://www.newscientist.com/article/2452686-amateur-sleuth-finds-largest-known-prime-number-with-41-million-digits/
https://www.mersenne.org/primes/?press=M136279841
https://www.theguardian.com/science/2003/dec/18/thisweekssciencequestions
https://www.livescience.com/physics-mathematics/mathematics/what-is-the-largest-known-prime-number