บทพิสูจน์ทฤษฎีบทพีทากอรัสของเด็กมัธยมปลาย

เมื่อวันที่ 27 ตุลาที่ผ่านมา วารสาร The American Mathematical Monthly ได้ตีพิมพ์งานวิจัยของเด็กมัธยมปลายชาวอเมริกันสองคนที่ขื่อว่า Ne'Kiya Jackson และ Calcea Johnson ที่พิสูจน์ทฤษฎีบทพีทาโกรัสด้วยตรีโกณมิติ

เรื่องนี้เป็นข่าวใหญ่ในวงการคณิตศาสตร์ มีหลายสำนักข่าวพูดถึงบทพิสูจน์ของพวกเธอ แต่คำถามที่น่าจะอยู่ในใจของคนนอกวงการคณิตศาสตร์หลายคนก็คือ สิ่งนี้มันพิเศษยังไงหรอ ก็แค่เด็กมัธยมปลายสองคนพิสูจน์ทฤษฎีที่เขาพิสูจน์กันมาได้เป็นพันปีแล้วเองนี่นา คนแค่ตื่นเต้นเพราะคนพิสูจน์เป็นเด็กหรือเปล่า ไม่ฮะ เรื่องมันไม่ใช่แค่นั้น

ผมเริ่มอธิบายอย่างนี้ก่อน ทฤษฎีบทพีทาโกรัสเป็นหนึ่งในทฤษฎีบททางคณิตศาสตร์ที่โด่งดังมาก คนทั้งโลกน่าจะต้องเคยได้เรียนเกี่ยวกับมันมา ถ้าใครลืมไปหมดแล้ว มันว่าด้วยความสัมพันธ์ระหว่างความยาวด้านทั้งสามของสามเหลี่ยมมุมฉาก ซึ่งคนที่ค้นพบและพิสูจน์มันได้เป็นคนแรกก็คือคุณพีทาโกรัส ที่มีชีวิตอยู่เมื่อสองพันกว่าปีก่อน และหลังจากนั้น ก็มีนักคณิตศาสตร์ทั่วโลกเสนอบทพิสูจน์ของทฤษฎีบทอันนี้ที่แตกต่างกันไว้มากมาย บ้างก็ใช้วิธีทางพีชคณิต บ้างก็ใช้วิธีทางเรขาคณิต เรียกได้ว่าทฤษฎีบทพีทาโกรัสน่าจะเป็นทฤษฎีที่มีวิธีพิสูจน์ที่แตกต่างกันมากที่สุดทฤษฎีหนึ่งเลย

จนเมื่อปี 1968 คุณ Elisha Loomis ได้เขียนหนังสือขึ้นมาเล่มหนึ่งชื่อว่า The Pythagorean Proposition โดยเธอรวบรวมวิธีการพิสูจน์ทฤษฎีบทพีทาโกรัสไว้ถึง 250 วิธีในหนังสือเล่มนี้ และในตอนท้ายของหนังสือ เธอได้เขียนเอาไว้ ใจความว่า

แม้ทฤษฎีบทพีทาโกรัสจะมีวิธีพิสูจน์อยู่มากมาย แต่มันไม่มีทางจะมีวิธีพิสูจน์ที่ใช้ตรีโกณมิติอย่างแน่นอน เพราะว่าสูตรพื้นฐานของตรีโกณมิตินั้นต่างถูกพิสูจน์มาจากทฤษฎีบทพีทาโกรัสทั้งนั้น ตรีโกณมิติจริงได้ก็เพราะทฤษฎีบทพีทาโกรัสจริง

ผมขอขยายความสิ่งที่เธอเขียนหน่อย สำหรับคนที่ไม่ได้อยู่ในแวดวงคณิตศาสตร์ คืออะไรก็ตามในคณิตศาสตร์เนี่ย จะเป็นจริงได้ก็ต่อเมื่อเราพิสูจน์แล้วว่ามันจริง ซึ่งการพิสูจน์ทางคณิตศาสตร์นั้นมักจะทำเป็นทอด ๆ เช่นเราพิสูจน์ทฤษฎีหนึ่งแล้วว่าเป็นจริง แล้วก็ใช้ทฤษฎีบทนั้นไปพิสูจน์อย่างอื่นต่อ อย่างนี้ไปเรื่อย ๆ ดังนั้นสิ่งที่อันตรายที่สุดในการพิสูจน์เป็นทอด ๆ แบบนี้คือการให้เหตุผลเป็นวงกลม หรือที่เรียกว่า circular reasoning

ตัวอย่างการให้เหตุผลเป็นวงกลมที่เห็นภาพง่าย ๆ ก็เช่น ถ้าผมบอกว่า หนังสือเล่มนี้ดีที่สุดในโลก เพราะไม่มีเล่มอื่นดีกว่ามัน อ้ะ แล้วถ้าถามว่าแล้วรู้ได้ยังไงว่าไม่มีเล่มอื่นดีกว่ามัน ผมก็จะบอกว่า ก็เพราะมันดีที่สุดในโลกไงล่ะ เห็นปัญหาไหมฮะ การให้เห็นผลเป็นวงกลมแบบนี้แปลว่าเราไม่ได้พิสูจน์มันจริง ๆ เพราะเราดันใช้สิ่งที่เป็นผลของมันมาเป็นเหตุ ซึ่งมันไม่ได้

ลองดูตัวอย่างนี้ฮะ ถ้าผมต้องการพิสูจน์ว่า มุมภายในของรูปสามเหลี่ยมใด ๆ มีค่าเท่ากับ 180 องศา

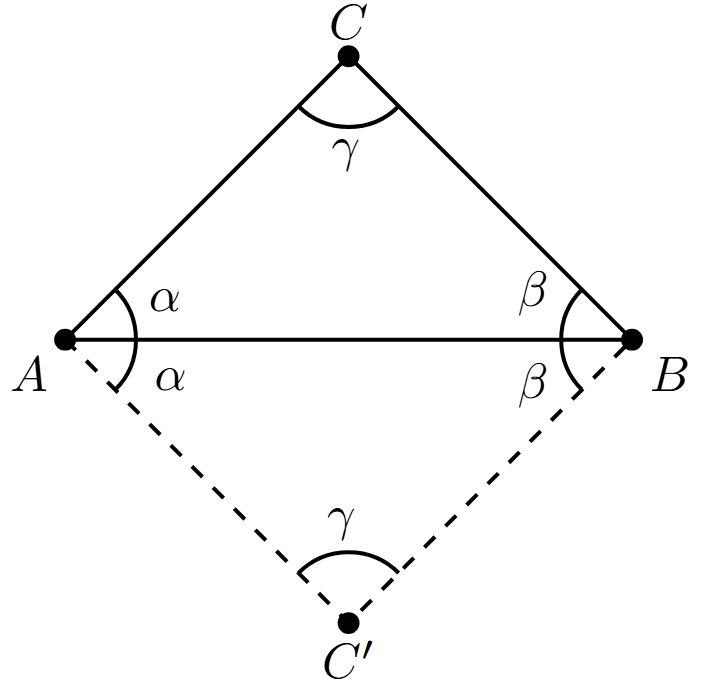
ผมเริ่มจากการวาดสามเหลี่ยม ABC ใด ๆ ขึ้นมา จากนั้นก็วาดจุด C' ให้สามเหลี่ยม ABC' เป็นเหมือนรูปสะท้อนของสามเหลี่ยมเดิม เราก็จะได้สี่เหลี่ยมด้านขนานขึ้นมาดังภาพ ทีนี้จากที่เรารู้อยู่ก่อนแล้วว่ามุมภายในของสี่เหลี่ยมใด ๆ นั้นจะเท่ากับ 360 องศาเสมอ และด้วยความที่สามเหลี่ยมสองรูปที่เรามีนั้นมุมเท่ากันเป็นคู่ ๆ ดังนั้นมุมมันเลยต้องเท่ากับ 360 มาหารด้วย 2 ดังนั้นเราจึงสรุปได้ว่ามุมภายในของรูปสามเหลี่ยมใด ๆ นั้นจะเท่ากับ 180 องศาเสมอนั่นเอง

บทพิสูจน์นี้ฟังดูดีมาก จนกระทั่งมีคนถามขึ้นมาว่า เอ้ะ แล้วเรารู้ได้ยังไงว่ามุมภายในของสี่เหลี่ยมใด ๆ นั้นจะเท่ากับ 360 องศาเสมอล่ะ เราก็จะบอกว่า อ๋อ เพราะเราเคยพิสูจน์มาแล้ว คนก็จะถามต่อว่า แล้วพิสูจน์ยังไงหรอ อ๋อ ง่ายมากเลย เพราะเรารู้ว่าสี่เหลี่ยมใด ๆ นั้นสามารถแบ่งเป็นสามเหลี่ยมสองรูปได้ และด้วยความที่มุมภายในของสามเหลี่ยมแต่ละรูปมันเท่ากับ 180 องศา รวมกันก็เลยเป็น 360 องศายังไงล่ะ !

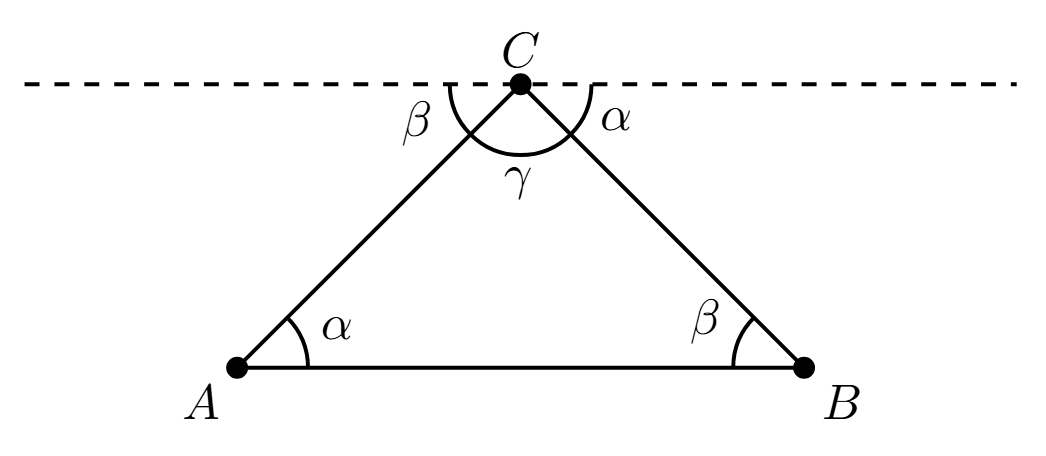
เห็นปัญหาไหมฮะ สิ่งนี้คือการให้เหตุผลเป็นวงกลม เพราะเราพิสูจน์มุมภายในของสามเหลี่ยมด้วยมุมภายในสี่เหลี่ยม แล้วก็พิสูจน์มุมภายในสี่เหลี่ยมด้วยสามเหลี่ยมอีกที แต่ถ้าเราเปลี่ยนวิธีพิสูจน์ใหม่ เการวาดสามเหลี่ยม ABC ใด ๆ ขึ้นมาเหมือนเดิม ลากเส้นขนานกับด้าน AB ให้ผ่านจุด C แล้วใช้ทฤษฎีเรื่องมุมแย้งของเส้นขนานเพื่อมาพิสูจน์ว่าผลบวกของมุมทั้งสามของสามเหลี่ยมนั้นจะเท่ากับขนาดของมุมบนเส้นตรง ซึ่งเท่ากับ 180 องศา ก็จะพิสูจน์เรื่องสามเหลี่ยมได้ แล้วจากนั้นก็ค่อยมาพิสูจน์เรื่องสี่เหลี่ยมต่อด้วยการใช้วิธีประกบกันเป็น 360 แบบนี้ก็จะไม่เกิดการให้เหตุผลเป็นวงกลม แค่เราต้องแน่ใจว่าเจ้าทฤษฎีเรื่องมุมแย้งที่เราอ้างใช้ตอนแรกนั้นไม่ได้พิสูจน์มาจากการที่สามเหลี่ยมมีมุม 180 องศา

ทีนี้กลับมาที่เรื่องพีทาโกรัส คือถ้าอิงจากที่คุณ Loomis เขียนไว้นั้น เธอบอกว่าสมบัติต่าง ๆ ในตรีโกณมิตินั้นถูกพิสูจน์มาจากพีทาโกรัสทั้งนั้น ดังนั้นการพยายามพิสูจน์พีทาโกรัสด้วยตรีโกณมิติจึงเป็นการให้เหตุผลเป็นวงกลมอย่างแน่นอน

แต่ปรากฎว่าคุณ Loomis คิดผิด เพราะในปี 2009 คุณ Jason Zimba ได้เสนอวิธีการพิสูจน์ทฤษฎีบทพีทาโกรัสด้วยตรีโกณมิติที่ไม่ใช่การให้เหตุผลเป็นวงกลม นั่นคือเขาสามารถพิสูจน์สูตรตรีโกณมิติที่ต้องใช้โดยไม่ใช้พีทาโกรัส และเอาสูตรนั้นมาใช้พิสูจน์ทฤษฎีบทพีทาโกรัสอีกที บทพิสูจน์นี้ถือเป็นบทพิสูจน์ทฤษฎีบทพีทาโกรัสวิธีแรกที่ใช้ตรีโกณมิติเท่าที่โลกนี้เคยมี และทำให้คำกล่าวของคุณ Loomis ที่เป็นจริงมาได้นานถึง 41 ปีต้องถูกทำลายลง

ต่อมา ในปี 2015 คุณ Nuno Luzia เสนอบทพิสูจน์ทฤษฎีบทพีทาโกรัสด้วยตรีโกณมิติวิธีที่สอง และใครจะเชื่อว่า บทพิสูจน์ทฤษฎีบทพีทาโกรัสด้วยตรีโกณมิติวิธีที่สาม จะถูกค้นพบโดยเด็กมัธยมปลายเท่านั้น ไม่สิ ผมต้องพูดว่า วิธีที่สาม สี่ ห้า หก และเจ็ดต่างหาก เพราะในงานวิจัยชิ้นนี้ พวกเธอไม่ได้เสนอวิธีการพิสูจน์แค่เพียงวิธีเดียว แต่เสนอมาถึง 5 วิธีพร้อมกันไปเลย และเผลอ ๆ จะมากกว่านั้นด้วยซ้ำ โดยพวกเธอได้พิสูจน์แล้วด้วยว่าวิธีทั้ง 5 ของพวกเธอนั้นไม่ใช่การให้เหตุผลเป็นวงกลมอย่างแน่นอน

เรื่องคือ เมื่อปี 2022 Ne'Kiya Jackson และ Calcea Johnson ได้เข้าแข่งขันตอบปัญหาทางวิชาการของโรงเรียนเพื่อชิงเงินรางวัล 500 ดอลล่า ซึ่งโจทย์ข้อโบนัสของการแข่งขันนั้นบอกว่าให้คิดวิธีการพิสูจน์ทฤษฎีบทพีทาโกรัสแบบใหม่ขึ้นมา พวกเธอก็เลยลองคิด จนออกมาเป็นบทพิสูจน์ที่ใช้ตรีโกณมิติที่ว่า จึงลองส่งดู ปรากฎว่าบทพิสูจน์ของเธอสองคนเข้าตาครูสอนคณิตศาสตร์ของโรงเรียน ทั้งสองจึงถูกชักชวนให้เอาพิสูจน์ที่ว่าไปเสนอในงานประชุมวิชาการของสมาคมคณิตศาสตร์อเมริกัน ตอนแรกพวกเธอก็ไม่แน่ใจ แต่คิดว่าลองดูก็ไม่เสียหาย

พวกเธอใช้เวลาสองสามเดือนต่อมาเพื่อปรับปรุงบทพิสูจน์นั้นในช่วงหลังเลิกเรียนและในวันหยุด ภายใต้คำแนะนำของคุณครูท่านนั้น ก่อนจะเอาไปในเสนอในงานประชุมวิชาการที่เต็มไปด้วยนักศึกษามหาวิทยาลัยและนักคณิตศาสตร์อาชีพ ผลคือ บทพิสูจน์ของพวกเธอสร้างความฮือฮาเป็นอย่างมาก เพราะอย่างที่ผมเล่าว่าแม้เราจะมีบทพิสูจน์ของทฤษฎีบทพีทาโกรัสอยู่มากมาย แต่เราเพิ่งมีบทพิสูจน์ที่ใช้ตรีโกณมิติอยู่แค่สองแบบเท่านั้น ทางผู้จัดการประชุมจึงมาติดต่อขอให้พวกเธอส่งผลงานนี้ไปตีพิมพ์ในวารสารทางวิชาการ เพื่อจะได้ให้ผู้เชี่ยวชาญตรวจสอบความถูกต้อง ก่อนที่จะได้รับคำยืนยัน และได้ตีพิมพ์ในที่สุด

ยิ่งไปกว่านั้น ในบทความที่ตีพิมพ์ พวกเธอไม่ได้เสนอบทพิสูจน์แค่อันแรกที่คิดได้อันเดียว แต่พวกเธอยังเสนอบทพิสูจน์เพิ่มอีก 4 แบบที่ไม่ซ้ำกัน รวมเป็น 5 แล้วยังเสนอถึงวิธีการสร้างบทพิสูจน์เพิ่มเติม ซึ่งสามารถสร้างบทพิสูจน์ที่แตกต่างกันได้อีกอย่างน้อย 5 วิธี เท่ากับว่าพวกเธอเสนอบทพิสูจน์อย่างน้อย 10 แบบ

เรื่องนี้แสดงให้เห็นว่า สิ่งต่าง ๆ ในคณิตศาสตร์ที่แม้จะดูเหมือนถูกศึกษามาอย่างทะลุปรุโปร่งแล้ว ก็ยังมีปริศนาที่รอการค้นพบอยู่อีกมาก และคนที่จะค้นพบของเจ๋ง ๆ พวกนั้นเป็นคนต่อไป อาจจะเป็นเด็กสักคน ที่ชอบนั่งทดอะไรขยุกขยิกบนกระดาษอยู่แถวบ้านคุณก็ได้

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

แหล่งอ้างอิง
บทความวิจัยตัวเต็ม
https://www.tandfonline.com/doi/full/10.1080/00029890.2024.2370240
เว็บไซต์รวมบทพิสูจน์ทฤษฎีบทพีทาโกรัส
https://www.cut-the-knot.org/pythagoras/
หนังสือ The Pythagorean Proposition (ประโยคที่ว่าอยู่ในหน้า 244)
https://files.eric.ed.gov/fulltext/ED037335.pdf
บทความที่เสนอวิธีการพิสูจน์ทฤษฎีบทพีทาโกรัสด้วยตรีโกณมิติคนแรก
https://www.academia.edu/105232762/On_the_Possibility_of_Trigonometric_Proofs_of_the_Pythagorean_Theorem
ข่าวเรื่อง Ne'Kiya Jackson และ Calcea Johnson
https://www.iflscience.com/teenagers-publish-trigonometric-proof-of-pythagoras-theorem-once-considered-impossible-76545
https://www.jpost.com/science/science-around-the-world/article-826623