เมื่อคุณพบว่าตัวเลขส่วนใหญ่ในโลกนี้ขึ้นต้นด้วยเลขหนึ่ง

ตอนผมไปเปิดบูธที่งาน Wit in Bangkok เมื่อเดือนที่ผ่านมา ผมได้ทำการทดลองเล็ก ๆ โดยให้คนที่มาร่วมงานบอกผมว่า ยอดเงินในบัญชีของเค้าตอนนั้น ขึ้นต้นด้วยเลขอะไร และภาพที่เห็นอยู่นี้คือผลลัพท์ที่เราได้ ซ้ายสุดคือหนึ่ง ไล่ไปจนถึงเก้า

ผลคือ เลขหลักแรกของยอดเงินในบัญชีของคนที่แวะเข้ามาบูธผมส่วนใหญ่เป็นเลข 1 อันดับต่อมาคือเลข 2 แล้วก็เหมือนจะค่อย ๆ ลดหลั่นกันลงไป คำถามคือสิ่งนี้เป็นเรื่องบังเอิญรึเปล่า

เดี๋ยวลองไปดูข้อมูลชุดอื่น ๆ กันก่อน

การกระจายตัวของเลขขึ้นต้น

เพื่อความเข้าใจที่ตรงกัน เลขขึ้นต้น หรือเลขหลักแรก ที่เรากำลังพูดถึงกันอยู่ตอนนี้คือตัวเลขหลักซ้ายสุดที่ปรากฎในตัวเลข เช่นเลขขึ้นต้นของ 18,483 คือ 1 และของ 4,387 คือ 4 ไม่สำคัญว่ามันจะอยู่ในหลักสิบร้อยพันหรืออะไร ขอให้มาเป็นหลักแรก

จากข้อมูลของ worldometers.info พบว่าเมื่อนำจำนวนประชากรของ 233 ประเทศทั่วโลกมานับดูเลยว่าขึ้นต้นด้วยเลข 1 กี่ประเทศ ขึ้นต้นด้วยเลข 2 กี่ประเทศ ไล่ไปแบบนี้ แล้ววาดเป็นกราฟออกมา และนี่คือกราฟที่ได้

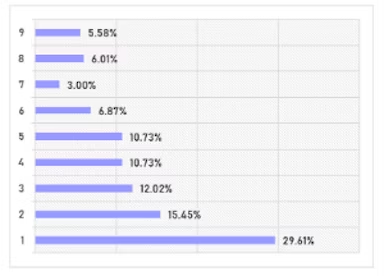
จะเห็นว่ามีจำนวนประเทศที่มีจำนวนประชากรขึ้นต้นด้วยเลข 1 มากที่สุดจริง ๆ ด้วย แล้วก็ค่อย ๆ น้อยลงลดหลั่นกันลงไป

ซึ่งเมื่อลองทำการทดลองแบบเดียวกันกับข้อมูลอย่างอื่นดูบ้าง อย่างเช่นข้อมูลระยะทางจากโลกไปยังดาวดวงต่าง ๆ ที่สว่างที่สุด 300 อันดับแรกบนท้องฟ้า (กราฟแรก) ข้อมูลตัวเลขรายจ่ายจำนวน 190,379 รายการของรัฐบาลสหราชอาณาจักรในช่วงเดือนพฤษภาคมถึงกันยายนปี 2010 (กราฟที่ 2) และข้อมูลจำนวนสิ่งพิมพ์ในห้องสมุดจำนวน 9,241 แห่งในประเทศสหรัฐอเมริกา (กราฟที่ 3)

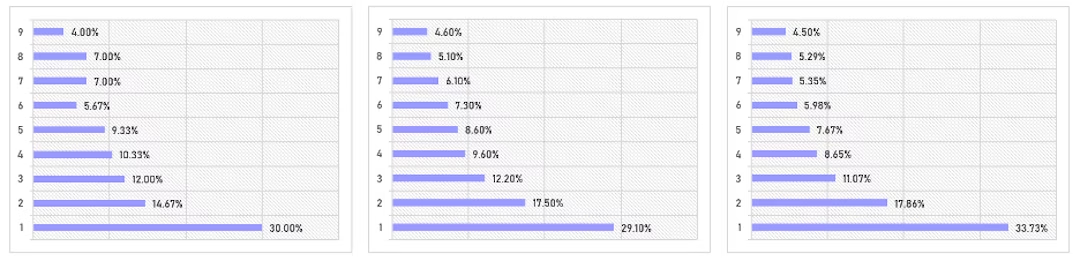
หลอนอยู่นะ คือมันไม่ใช่แค่ว่าทุกอันขึ้นต้นด้วยเลข 1 เยอะที่สุดเหมือนกันแล้ว แต่มันอยู่ที่ราว 30% เหมือนกันด้วย ยิ่งไปกว่านั้นคือ จำนวนข้อมูลที่ขึ้นต้นด้วยเลขหลักอื่น ๆ ก็ยังลดหลั่นกันลงมาด้วยอัตราส่วนคล้าย ๆ กันด้วยนี่สิ

ข้อมูลสี่ชุดที่ไม่มีความเกี่ยวข้องอะไรกันเลยสักนิด ไม่มีความคล้ายกันสักอย่าง ปริมาณก็คนละปริมาณ หน่วยก็คนละหน่วย บางชุดเป็นตัวเลขแค่ไม่กี่พัน ในขณะที่บางข้อมูลเป็นเลขหลักล้าน ๆ แต่กลับมีการกระจายของตัวเลขที่ขึ้นต้นออกมาเหมือนกันขนาดนี้ได้ยังไง

กฎของเบนฟอร์ด

ความจริงแล้วมีคนทำการทดลองแบบนี้มาก่อนผมตั้งแต่เมื่อ 86 ปีที่แล้ว คุณ Frank Benford วิศวกรไฟฟ้าชาวอเมริกาได้ลองเอาข้อมูล 20 ชุดที่ดูไม่มีอะไรเกี่ยวข้องกันเลยมานั่งนับว่าเลขส่วนใหญ่ในนั้นขึ้นต้นด้วยอะไร และผลคือมันขึ้นด้วยหนึ่งหมดเลย

เขาได้สรุปออกมาเป็นกฎ ที่ต่อมาถูกเรียกว่ากฎของเบนฟอร์ด ว่าการกระจายของเลขหลักแรกของข้อมูลใด ๆ ในโลกนี้นั้น “น่าจะ” เป็นไปตามอัตราส่วนดังกราฟต่อนี้

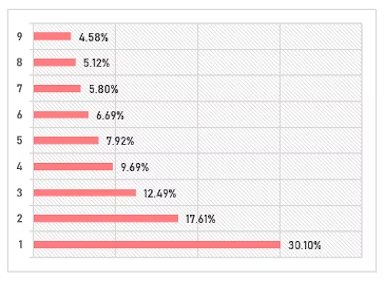
หรือพูดให้ดูเป็นคณิตศาสตร์หน่อยก็คือเป็นไปตามสูตร

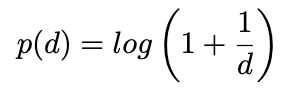
สำหรับ d=1,2,…,9

แน่นอนว่าหลังจากเบนฟอร์ดตีพิมพ์บทความเรื่องนี้ออกมา ก็มีคนทดลองเอาข้อมูลตัวเลขต่าง ๆ มากมายมาทดลองหาการกระจายของเลขขึ้นต้นว่าสอดคล้อง (หรือใกล้เคียง) กับกฎของเบนฟอร์ดหรือไม่

ข้อสังเกตที่น่าสนใจอย่างหนึ่งเกี่ยวกับกฎของเบนฟอร์ดก็คือ กฎนี้นั้นจริงโดยไม่ขึ้นอยู่กับหน่วย เช่นหากเราเก็บข้อมูลความสูงของประชากรมาทดลอง หากข้อมูลชุดนี้สอดคล้องกับกฎของเบนฟอร์ดแล้ว ไม่ว่าจะเก็บมาในหน่วยเซนติเมตร หน่วยฟุต หรือหน่วยวัดแบบไหนก็ตาม มันก็จะยังสอดคล้องอยู่ หมายความว่าการกระจายของเลขหลักแรกก็จะเป็นกราฟหน้าตาเหมือนเดิมอยู่ดี ใครที่นึกตามไม่ทันว่าเรื่องนี้มันน่าตื่นเต้นยังไง ลองคิดตามว่า 1 ฟุตมีค่าประมาณ 30 เซนติเมตรนะ ดังนั้นหากเดิมเราเก็บข้อมูลมาได้ 12 ฟุต ซึ่งขึ้นต้นด้วย 1 เมื่อแปลงเป็นเซนติเมตรจะกลายเป็นประมาณ 360 ซึ่งขึ้นต้นด้วยไปแล้ว 3 นะ ตามสามัญสำนึก รูปการกระจายตัวของเลขขึ้นต้นมันก็น่าจะเปลี่ยนไปรึเปล่า ซึ่งความจริงคือไม่เปลี่ยน เราสามารถพิสูจน์ได้ว่า ถ้าเรามีข้อมูลที่สอดคล้องกฎของเบนฟอร์ดอยู่แล้ว ไม่ว่าเราจะแปลงหน่วยของข้อมูลนั้นไปยังไง รูปกราฟของมันจะยังคงออกมาตามกฎของเบนฟอร์ดเหมือนเดิม

แล้วเรื่องนี้มันน่าสนใจยังไง

ในทางสถิติ เราเชื่อว่าข้อมูลแต่ละอย่างนั้นมีรูปแบบที่ต่างกันออกไป ตามแต่ธรรมชาติของมัน แม้ว่าในบางครั้งเราจะสามารถสร้างกฎหลวม ๆ ขึ้นมาเพื่ออธิบายจุดร่วมของข้อมูลที่คล้ายกัน เช่นระยะเวลาที่รอต่อคิวกด ATM กับระยะเวลาที่ใช้รอรถเมล์ ที่อาจจะไม่ได้มีรูปแบบเหมือนกันซะทีเดียว แต่ความที่มันเป็นระยะเวลาการรอเหมือนกัน รูปแบบของข้อมูลสองชุดนี้ก็อาจจะคล้ายกันในบางแง่ แต่เราคงไม่หวังว่าข้อมูลที่ดูต่างกันคนละโยชน์อย่างจำนวนประชากรของแต่ละประเทศในโลก ข้อมูลระยะห่างจากดวงดาว กับข้อมูลรายจ่ายของรัฐบาลอังกฤษ จะมามีรูปแบบบางอย่างที่คล้ายกันได้ขนาดนี้

การค้นพบนี้ของเบนฟอร์ดจึงกำลังบอกเราว่า อาจจะมีจุดร่วมบางอย่างที่เราไม่รู้ซ่อนอยู่เบื้องหลังข้อมูลต่าง ๆ หรือพูดให้ดูใหญ่โตหน่อยก็คือ จริง ๆ แล้วมันอาจจะมีกฎหนึ่งเดียวบางอย่างที่สามารถใช้อธิบายข้อมูลทั้งโลกนี้ก็ได้

มีการนำกฎของเบนฟอร์ดนี้ไปใช้งานกันอย่างแพร่หลาย หนึ่งในตัวอย่างที่โด่งดังคือการจับทุจริตการฉ้อโกงของบัญชีของบริษัทแห่งหนึ่งในสหรัฐอเมริกาเมื่อปี 1972 ของนายฮัล วาเรียน (Hal Varian) โดยเขาพบว่ามีการปลอมแปลงข้อมูลขึ้นเพราะข้อมูลที่ออกมานั้นไม่สอดคล้องกับกฎของเบนฟอร์ดอย่างมากจนผิดปกติ

นอกจากนี้กฎของเบนฟอร์ดถูกนำมาใช้ในการวิเคราะห์ผลการเลือกตั้งหลายครั้งเพื่อตรวจหาความผิดปกติในการลงคะแนนเสียง โดยแนวคิดคือ หากตัวเลขที่ได้จากผลการเลือกตั้งมีการทุจริตหรือปลอมแปลงขึ้นมา ข้อมูลเหล่านั้นอาจไม่สอดคล้องกับการกระจายตัวเลขตามกฎของเบนฟอร์ด เช่น จำนวนผู้ลงคะแนนในแต่ละเขต หรือจำนวนคะแนนเสียงที่ผู้สมัครได้รับในแต่ละสถานีเลือกตั้ง ควรจะมีการกระจายของตัวเลขที่สอดคล้องกับกฎนี้ แต่ถ้าพบว่ามีการเบี่ยงเบนอย่างมีนัยสำคัญ อาจเป็นสัญญาณของการปลอมแปลงข้อมูลหรือทุจริต

แต่ในบางกรณี ผลที่ได้ยังเป็นที่ถกเถียงกันว่าวิธีนี้สามารถใช้ตรวจสอบการทุจริตได้อย่างแม่นยำจริงหรือไม่ เช่นในการเลือกตั้งของสหรัฐอเมริกาที่เป็นแบบสองพรรคใหญ่ ดังนั้นคะแนนเสียงของสองพรรคใหญ่นั้นจะต้องบวกกันได้จำนวนประชากรรวมของแต่ละเขา ถ้าคะแนนเสียงของพรรคหนึ่งเป็นไปตามกฎของเบนฟอร์ดแล้ว ก็ยากที่ของอีกคนจะเป็นไปตามด้วย

แล้วทำไมมันถึงเป็นอย่างนั้น

ข้อมูลที่สอดคล้องกับกฎของเบนฟอร์ดนั้น จะต้องเป็นข้อมูลที่มีการกระจายตัวอยู่ในหลาย ๆ หลักมากพอ ไม่ใช่ข้อมูลจำพวกส่วนสูงหรือน้ำหนักของคนที่กระจุกตัวกันอยู่ในหลักเดียว และต้องเป็นตัวเลขที่ที่เป็นปริมาณของอะไรสักอย่าง ไม่ใช่เลขที่เป็นลำดับหรือถูกสร้างขึ้นมา เช่นพวกรหัสนักศึกษา รหัสไปรษณีย์ เบอร์โทรศัพท์ หรือรหัสผ่านเอทีเอ็มอะไรทำนองนั้น

มีความพยายามจะอธิบายด้วยทฤษฏีทางความน่าจะเป็นและสถิติหลายอย่าง เช่น เราพิสูจน์ได้ว่าการเอาข้อมูลที่กระจายตัวอย่างสม่ำเสมอมาเขียนบนล็อกสเกล มันก็จะออกมาสอดคล้องกับกฎของเบนฟอร์ดพอดี ดังนั้นสำหรับชุดข้อมูลที่มีลักษณะการเติบโตแบบเอ็กซ์โปเนนเชียล เช่น รายได้และราคาหุ้น นี่ถือว่าเป็นสมมติฐานที่ฟังดูสมเหตุสมผล แต่เราก็พบว่ายังมีชุดข้อมูลอื่น ๆ ที่ไม่ได้ชัดเจนว่าเติบโตแบบเอ็กซ์โปเนนเชียล แต่ยังสอดคล้องกับกฎของเบนฟอร์ดอยู่อีก

แถมท้าย ใครที่สนใจเห็นว่ามีข้อมูลแปลก ๆ อะไรอีกบ้างที่สอดคล้องกฎนี้ สามารถลองเข้าไปเล่นที่เว็บไซด์นี้ได้เลย http://testingbenfordslaw.com/

และสำหรับใครที่อยากช่วยสนับสนุนเพจและเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์อย่างนี้ต่อไป สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

แหล่งอ้างอิง
https://www.scientificamerican.com/article/what-is-benfords-law-why-this-unexpected-pattern-of-numbers-is-everywhere/
https://statisticsbyjim.com/probability/benfords-law/