เมื่อบวกเลขไปถึงอนันต์ตัว อยู่ดี ๆ ลำดับก็สำคัญขึ้นมา
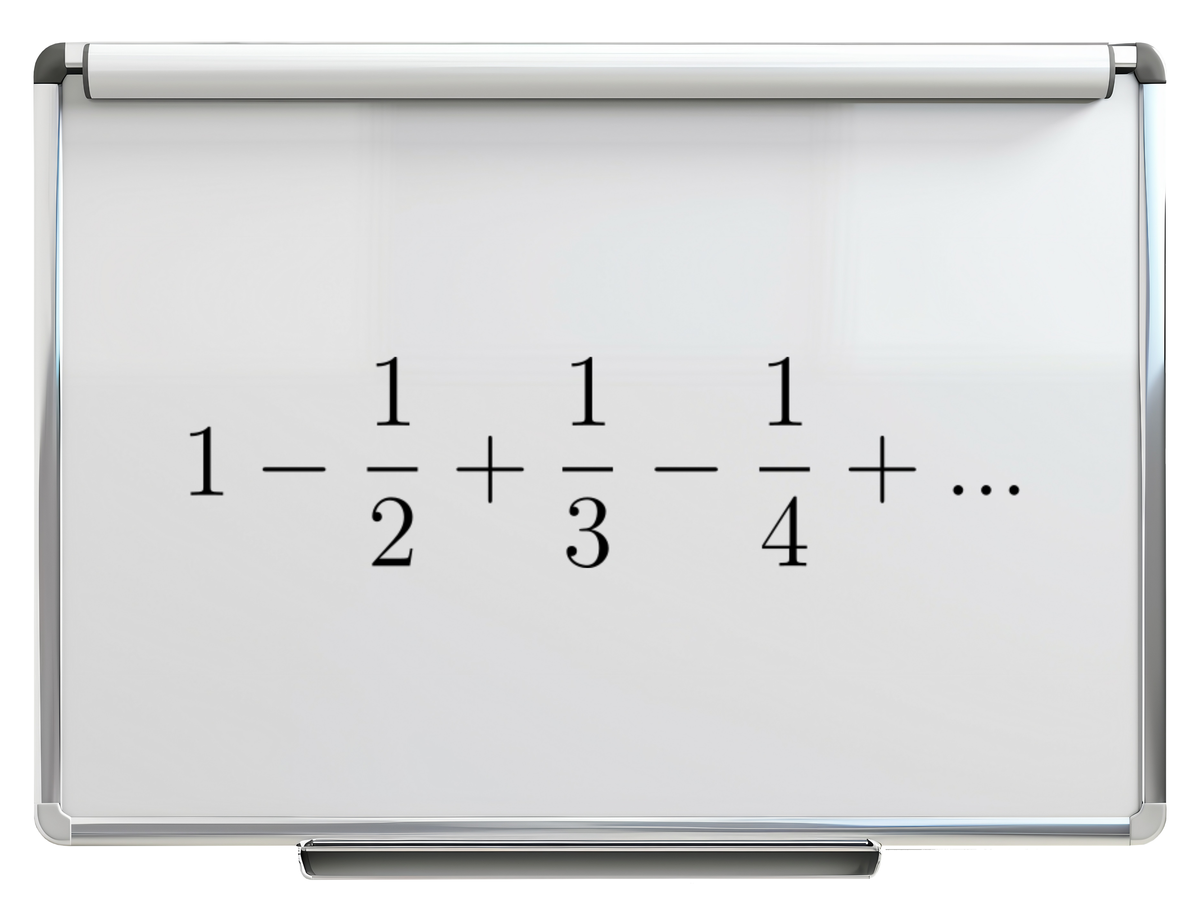
เราเรียนกันมาตั้งแต่ชั้นประถมแล้วว่าการบวกนั้นสามารถสลับที่ได้ เช่น 2+3 หรือ 3+2 ก็จะให้ผลลัพธ์เป็น 5 เหมือนกัน สิ่งนี้เรียกเท่ ๆ ว่ากฎการสลับที่ นอกจากนี้เรายังมี กฎการเปลี่ยนกลุ่ม ที่บอกเราว่าถ้าต้องบวกเลขหลาย ๆ ตัว เราจะหยิบคู่ไหนมาบวกกันก่อนก็ได้ เช่น 1+2+3 นั้น จะเอา 1+2 ก่อนให้เป็น 3 แล้วค่อยไปบวก 3 หรือจะเอา 2+3 ก่อน แล้วค่อยเอาไปบวก 1 ก็จะได้คำตอบเป็น 6 เหมือนกันหมด ดังนั้น เมื่อเราเจอโจทย์การบวก เราก็สามารถเลือกได้ตามใจเลยว่าจะบวกตัวเลขไหนก่อนหลัง
แต่สิ่งนี้อาจจะไม่จริงอีกต่อไป เมื่อเราบวกเลขไปถึงอนันต์ครั้ง
การบวกอนันต์หรือที่เรียกกันในคณิตศาสตร์ว่าอนุกรมอนันต์ คือการนำลำดับของตัวเลขมาบวกกัน เช่น 1+2+3+4+… ซึ่งการบวกเลขไปอนันต์ครั้งนั้นอาจจะไม่ได้หาค่าได้เสมอไป
เราจะเรียกผลบวกอนันต์ครั้งที่หาคำตอบได้ว่ามันลู่เข้า อย่างเช่น
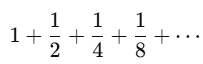
ซึ่งเรารู้ว่ามันได้ 2
และเรียกผลบวกอนันต์ครั้งที่หาคำตอบไม่ได้ว่ามันลู่ออก อย่างเช่น
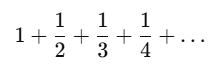
ที่บวกไปแล้วมันดันได้ค่าเป็นอนันต์เฉยเลย หรือแบบ
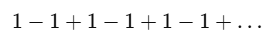
ที่ลู่ออกเพราะว่าผลบวกมันแกว่งไปแกว่งมาระหว่าง 0 และ 1
ทีนี้ ความพิเศษของการไปอนันต์ครั้งก็คือ ลำดับของการบวกนั้นมีผล อย่างเช่นผลบวกต่อไปนี้ซึ่งมีชื่อเรียกเท่ ๆ ว่าผลบวกฮาร์โมนิกสลับ
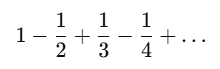
คือถ้าเราบวกมันไปตรง ๆ ที่แปลว่าเริ่มต้นจาก 1 ลบ 1/2 แล้วเอามาบวก 1/3 แล้วลบ 1/4 ไล่ไปเรื่อย ๆ ตามลำดับนี้ ค่าที่เราจะได้คือ ln(2) ฮะ ผมจะไม่ทำให้ดูนะว่ามันได้ ln(2) แต่ขอ plot เป็นกราฟให้ดูแทน
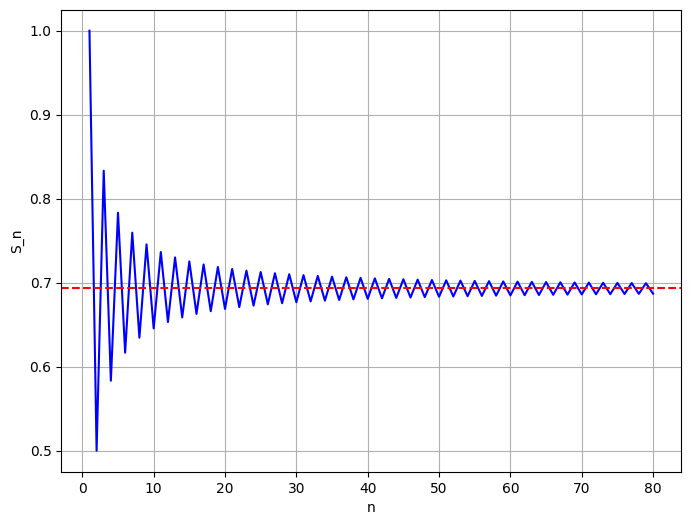
ทีนี้ ถ้าผมนึกคึก สลับลำดับและจัดกลุ่มการบวกใหม่นิดหน่อย เป็นดังนี้
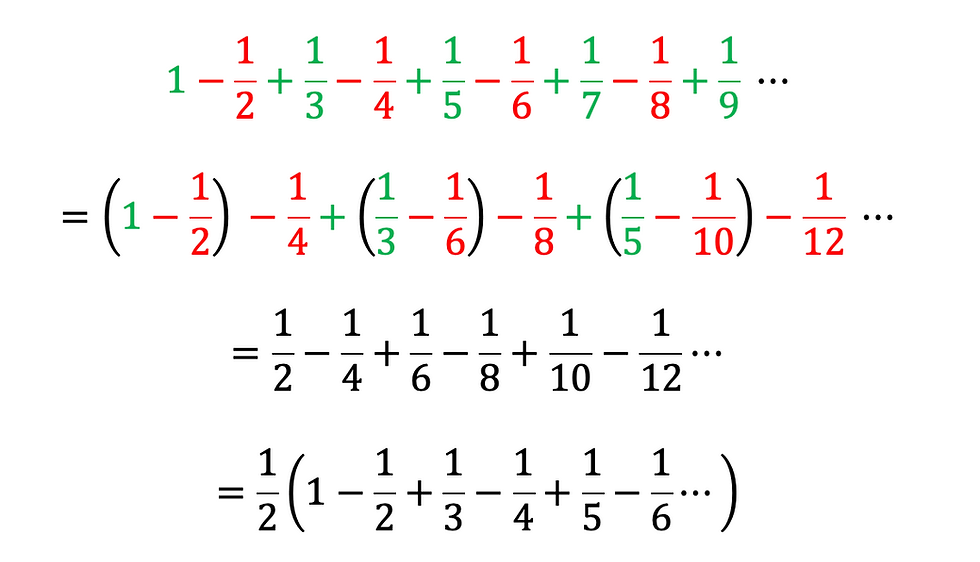
ผลที่ได้คือมันจะกลายเป็นแค่ครึ่งเดียวของผลบวกตัวเดิมของเรา ซึ่งคือ (1/2)ln(2) เฉยเลย นั่นแหละฮะที่ผมบอก แค่เราสลับตำแหน่งและจัดกลุ่มใหม่ ผลบวกที่ได้ก็เปลี่ยนไปแล้ว ซึ่งพอมาถึงตรงนี้ บางคนที่อาจอยู่ก็อาจจะกำลังรู้สึกว่า โอ้ว แย่แล้ว แปลว่าคณิตศาสตร์ที่ฉันเรียนมาทั้งหมดนั้นผิดหรอ ครูที่สอนกฎการสลับที่กับกฎการจัดกลุ่มนั้นสอนมั่วมาตลอดเลยหรอออ
ใจเย็นฮะ ไม่มีอะไรผิดทั้งนั้นแหละ กฎทั้งสองข้อที่เราเรียนมาทั้งสองข้อนั้นไม่ได้ผิดอะไรเลย มันยังคงจริงอยู่ในโลกของการบวกทั่ว ๆ ไปที่ไม่ใช่การบวกอนันต์ครั้ง คุณจะบวกเลขสองตัว สามตัว สิบตัว หรือแสนล้านตัว กฎสองข้อนั้นก็ยังจริงอยู่ แค่ต้องไม่ใช่กับการบวกอนันต์ครั้งเท่านั้นเอง
มาถึงตรงนี้ มีสิ่งที่น่าสนใจอยู่สองข้อฮะ
ข้อแรก คือนอกจาก ln(2) และ (1/2)ln(2) แล้ว เรายังสามารถจัดเรียงผลบวกฮาร์โมนิกสลับนี้ให้ออกมาเป็นเท่าไรก็ได้ คือจิ้มมาได้เลยว่าคุณชอบเลขอะไร ผมจะสามารถจัดเรียงผลบวกนี้ให้ออกมาเท่ากับเลขที่คุณจิ้มได้เลย หรือแม้แต่จะเรียงให้มันลู่ออกก็ยังทำได้เลย แน่นอนว่าผมจะไม่พิสูจน์ข้อความนี้ตรงนี้ แต่ผมอยากให้คุณลองไปหาอ่าน เชื่อผมเถอะว่ามันไม่ได้ยาก
และสอง ไม่ได้มีแค่ผลบวกฮาร์โมนิกสลับนี้เท่านั้นที่ทำแบบนี้ได้ แต่ความจริงแล้วผลบวกที่มีสมบัติลู่เข้าอย่างมีเงื่อนไขทุกอันนั้นทำแบบนี้ได้หมดเลย สมบัติการลู่เข้าอย่างมีเงื่อนไขนั้นบางคนอาจจะเคยได้ยินคุ้น ๆ ผ่านหูมาบ้างตอนเรียนแคลคูลัส 2 แต่ถ้าใครลืม มันคือผลบวกที่ตัวมันเองลู่เข้า แต่ผลบวกของค่าสัมบูรณ์ของมันลู่ออกนั่นเอง
ข้อค้นพบนี้ถูกเรียกว่า Riemann Rearrangement Theorem ซึ่งพูดเป็นภาษาคณิตศาสตร์ได้ว่า อนุกรมที่ลู่เข้าแบบมีเงื่อนไขจะสามารถจัดเรียงลำดับพจน์ใหม่ของอนุกรมเพื่อให้ลู่เข้าไปยังค่าที่กำหนดใด ๆ ก็ได้ หรือให้ลู่ออกไปยังอนันต์หรือลบอนันต์ก็ได้
สิ่งนี้กำลังบอกเราว่า อนันต์นั้นเป็นคอนเซ็ปที่ซับซ้อน การทำอะไรแบบเข้าใกล้อนันต์ ไม่ว่าจะเป็นใกล้มาก ๆ จนใกล้อนันต์ ถี่มาก ๆ จนใกล้อนันต์ หรืออย่างในกรณีนี้ที่เราบวกไปเยอะมาก ๆ จนถึงอนันต์ นั้นสามารถทำให้เกิดสิ่งที่ขัดกับสามัญสำนึกของเราได้เสมอ เพราะสามัญสำนึกเกี่ยวกับจำนวนของเรานั้นอยู่บนฐานของการคำนวณสิ่งต่าง ๆ รอบตัว ซึ่งไม่ได้ต้องไปข้องเกี่ยวกับอนันต์อยู่แล้ว ดังนั้นเมื่อต้องทำอะไรเกี่ยวกับอนันต์ เราจึงจะรู้สึกว่ามันขัดกับความคุ้นเคยไปหมด นี่จึงเป็นเหตุผลที่ทำให้หลาย ๆ คนรู้สึกว่าแคลคูลัสนั้นเป็นวิชาที่ยาก เพราะรากฐานสำคัญของแคลคูลัสนั้นก็คือการคำนวณสิ่งต่าง ๆ ในระดับอนันต์ทั้งนั้นเลย
และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ
แหล่งอ้างอิง
https://www.cut-the-knot.org/arithmetic/algebra/RiemannRearrangementTheorem.shtml
https://www.meanderingwithmaths.com/post/one-sum-any-number-riemann-s-rearrangement-theorem
https://sites.math.washington.edu/~morrow/335_16/history%20of%20rearrangements.pdf