เข้าคิวแถวเดียวหรือหลายแถว แบบไหนเร็วกว่ากัน

ผมเล่าเรื่องปัญหาการเข้าคิวแถวเดียวหรือหลายแถวทุกครั้งที่มีโอกาส และเนื่องจากว่าผมกำลังต้องขายคอร์ส Probability for Data Science ที่ทำกับทาง Skooldio ผมจึงจะเล่ามันที่นี่อีกครั้ง

ทุกคนน่าจะเคยเข้าคิว ซื้อตั๋วหนัง จ่ายเงินร้านสะดวกซื้อ สั่งอาหารร้านฟาสต์ฟู้ด หรือตรวจกระเป๋าเข้าสนามบิน และเผื่อใครไม่ทันได้สังเกต การต่อคิวทำอะไรพวกนี้มันจะมีอยู่สองแบบฮะ คือแบบหลายแถว (Multiple Queues) มีกี่เคาน์เตอร์ก็ตั้งแถวไปเลยตามนั้น หนึ่งแถวสำหรับหนึ่งเคาน์เตอร์ ร้านสะดวกซื้อกับร้านฟาสต์ฟู้ดส่วนใหญ่เป็นแบบนี้ กับอีกแบบคือแบบแถวเดียว (Single Queue) ที่ทุกคนจะกองรวมกันอยู่ในแถวเดียว แล้วเคาน์เตอร์ไหนว่างปุ๊บ คนแรกก็จะเข้าไป โรงหนังกับตรวจกระเป๋าเข้าสนามบินส่วนใหญ่เป็นแบบนี้

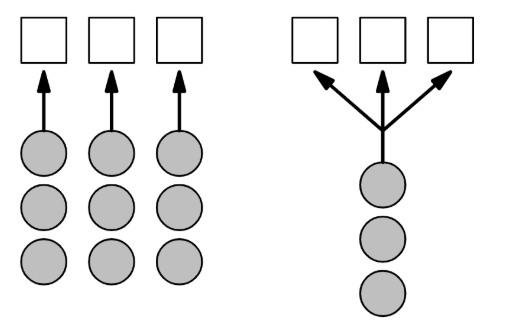
แล้วแบบไหนดีกว่ากัน

ลองคิดแบบง่าย ๆ ดูก่อน การเข้าคิวแบบแถวเดียวแล้วไปแยกนั้นน่าจะดีกว่า แม้ว่าแว้บแรกลูกค้าจะรู้สึกว่าแถวยาวจัง แต่พอเห็นว่าแถวมันเคลื่อนไปได้เร็ว ก็จะรู้สึกโอเคมากขึ้น เทียบกับแบบแยกแถวไปเลย ที่แม้ว่าแว้บแรกจะรู้สึกว่าแถวนั้นสั้นกว่า แต่หากเลือกแถวผิดแล้วเจอคนข้างหน้าช้าจนมีแถวอื่นแซงไป กลายเป็นว่าช้ากว่า และพาลทำให้รู้สึกไม่ดีเปล่า ๆ

แต่คำถามสำคัญก็คือ ไอ้ความคิดที่ว่า "การเข้าคิวแบบแถวเดียวนั้นทำให้ลูกค้าเคลื่อนไปได้เร็วกว่า" นั้นเป็นแค่ความรู้สึกรึเปล่า หรือมันเป็นแบบนั้นจริง ๆ

เพื่อตอบคำถามนี้ เราสมมติให้เวลาที่ลูกค้าแต่ละคนใช้ที่เคาน์เตอร์เป็นค่าที่สุ่มด้วยการแจกแจงแบบเอ็กซ์โพเนนเชียล โดยมีค่าเฉลี่ย M นาทีต่อคนเท่ากันหมด และสมมติว่าตอนคุณเดินเข้ามาในแถว ทุกเคาน์เตอร์กำลังติดลูกค้าอยู่ และมีคนรอในแถวอยู่ก่อนหน้าคุณ 9 คน

ถ้าใช้ระบบหลายแถว แสดงว่าลูกค้า 9 คนนั้นก็จะแบ่งไปแถวละ 3 คน และด้วยความที่คุณไม่รู้ว่าต้องไปต่อแถวไหนดี เพราะไม่รู้ว่าใครจะเร็วหรือช้าแค่ไหน คุณก็เลยไปยืนสุ่ม ๆ สักแถว เอาเป็นแถวแรกเลย เพราะในแถวมีคนอยู่ 3 คนก่อนหน้าคุณ และแต่ละคนใช้เวลาเฉลี่ย L นาที แสดงว่าคุณต้องรอเฉลี่ยไป 3L นาที

แล้วถ้าใช้ระบบแถวเดียวล่ะ ทั้ง 9 คนนี้ก็จะมากองอยู่แถวเดียวกัน แต่ละคนใช้เวลาเฉลี่ย L นาที ก็ต้องรอไปถึง 9L นาทีเลยหรอ ช้ากว่ามากเลยนะ

ไม่ใช่ฮะ คิดแบบนี้ไม่ได้ เพราะเราไม่ได้มีแค่ 1 แต่เรามีถึง 3 เคาน์เตอร์ แปลว่าลูกค้าคนแรกสุดของแถวแค่ต้องรอใครก็ได้สักคนที่เคาน์เตอร์ให้ทำธุระเสร็จ ใครก็ได้ ขอแค่เสร็จคนเดียว แถวก็จะเริ่มขยับทันที ซึ่งใช้เวลาแค่ L/3 เท่านั้น และที่เราเดากันไว้ว่าการเข้าคิวแบบแถวเดียวจะทำให้แถวเคลื่อนไวกว่านั้นก็เป็นเรื่องจริง

แต่แค่แถวเคลื่อนที่เร็วนั้นดีจริงหรอ เพราะถึงระบบหลายแถวจะเคลื่อนช้า แต่อย่าลืมว่าคนในแต่ละแถวก็น้อย ลองคูณดูสิ ใช้เวลาคนละ L มี 3 คนก็เป็น 3L แต่แบบแถวเดียว เคลื่อนที่เร็วมาก ใช้เวลาคนละ L/3 แต่มีตั้ง 9 คน สรุปก็เป็น 3L เท่ากัน

ถูกฮะ ถูกต้องเลย ถ้ามองในมุมค่าเฉลี่ย สุดท้ายไม่ว่าจะตั้งแถวแบบไหน เวลาที่เราต้องใช้รอก็จะออกมานานเท่ากัน แต่อย่าลืมว่าค่าเฉลี่ยไม่ใช่ทุกอย่าง

เพราะถ้าเราไปมองในแง่ของความแปรปรวน เราจะพบว่า ความแปรปรวนของเวลาที่ต้องรอของระบบหลายคิวคือ 3L² ส่วนของระบบคิวเดียวคือ L² เท่านั้นเอง ผมขออนุญาตละที่มีการคำนวณความแปรปรวนนะ คิดซะว่าเป็นการบ้านก็ได้ แต่จากค่าที่ได้นี้บอกอะไรเรา มันกำลังบอกว่า แม้ทั้งการเข้าคิวทั้งสองระบบนั้นใช้เวลาเท่ากัน แต่การใช้ระบบหลายคิวนั้นจะทำให้บางคนใช้เวลาน้อยกว่าค่าเฉลี่ยไปมาก และบางคนใช้เวลานานกว่าค่าเฉลี่ยไปมาก ต่างจากแบบคิวเดียวที่ทุกคนจะใช้เวลาพอ ๆ กันทั้งหมด ซึ่งนั่นก็คือที่มาของความรู้สึกแย่ที่อาจเกิดเมื่อเห็นคนอื่นไปได้ไวกว่าที่เราเดากันไว้ตั้งแต่ตอนแรกนั่นแหละ

สรุปก็คือ คณิตศาสตร์กำลังยืนยันว่าที่เราคิดแบบง่าย ๆ กันไว้ตอนแรกนั้นถูกอยู่แล้ว แล้วถ้าอย่างนั้นจะใช้คณิตศาสตร์ให้ยุ่งยากทำไมถ้าคิดง่าย ๆ เอาก็ถูกเหมือนกัน? คำตอบก็คือ เราเดาถูกเพราะสถานการณ์นี้มันง่าย แค่มีเคาน์เตอร์ คนในแถว แล้วก็วิธีจัดแถว

แต่ถ้าสถานการณ์มันซับซ้อนกว่านั้นล่ะ อย่างในสนามบินที่ต้องตรวจกระเป๋า ตรวจพาสปอร์ต และผ่านด่าน ตม. ซึ่งแต่ละจุดใช้เวลาไม่เท่ากัน หรือในโรงพยาบาลที่ต้องลงทะเบียน วัดสัญญาณชีพ พบแพทย์ และรับยา ลำดับของขั้นตอนก็มีผลต่อเวลารอโดยรวม สถานการณ์เหล่านี้ซับซ้อนเกินกว่าจะใช้แค่การคิดง่าย ๆ ด้วยความรู้สึก และสิ่งที่จะช่วยให้เราเข้าใจระบบที่มีความผันผวน และสามารถตัดสินใจได้อย่างมีประสิทธิภาพนั้นจะเป็นอะไรได้ ถ้าไม่ใช่ความรู้เรื่องความน่าจะเป็น

คอร์ส Probability for Data Science โดยผมเอง พรรษ วติวุฒิพงศ์ เจ้าของเพจคณิตศาสตร์อย่างที่ควรจะเป็น จะสอนวิธีเปลี่ยนความไม่แน่นอนให้กลายเป็นสิ่งที่เราควบคุมได้ เข้าใจคอนเซ็ปพื้นฐานของความน่าจะเป็น ตัวแปรสุ่ม และการทำ simulation จากข้อมูล

ซึ่งช่วงเปิดตัวนี้ทาง skooldio เขาลดราคาให้แบบสุด ๆ ถึง 30% จาก 1,990 บาท เหลือเพียง 1,390 บาท โดยใส่โค้ด PDS_EB30 ได้ที่

https://www.skooldio.com/courses/probability-for-data-science

เมื่อสมัครภายใน 7 เมษายนนี้เท่านั้น

สอบถามรายละเอียดเพิ่มเติมได้ที่เพจ https://www.facebook.com/skooldio

แล้วพบกันในคอร์สนะครับ