คิดสูตรอาหารที่ไม่เคยมีมาก่อนในโลกนี้ด้วย Topology

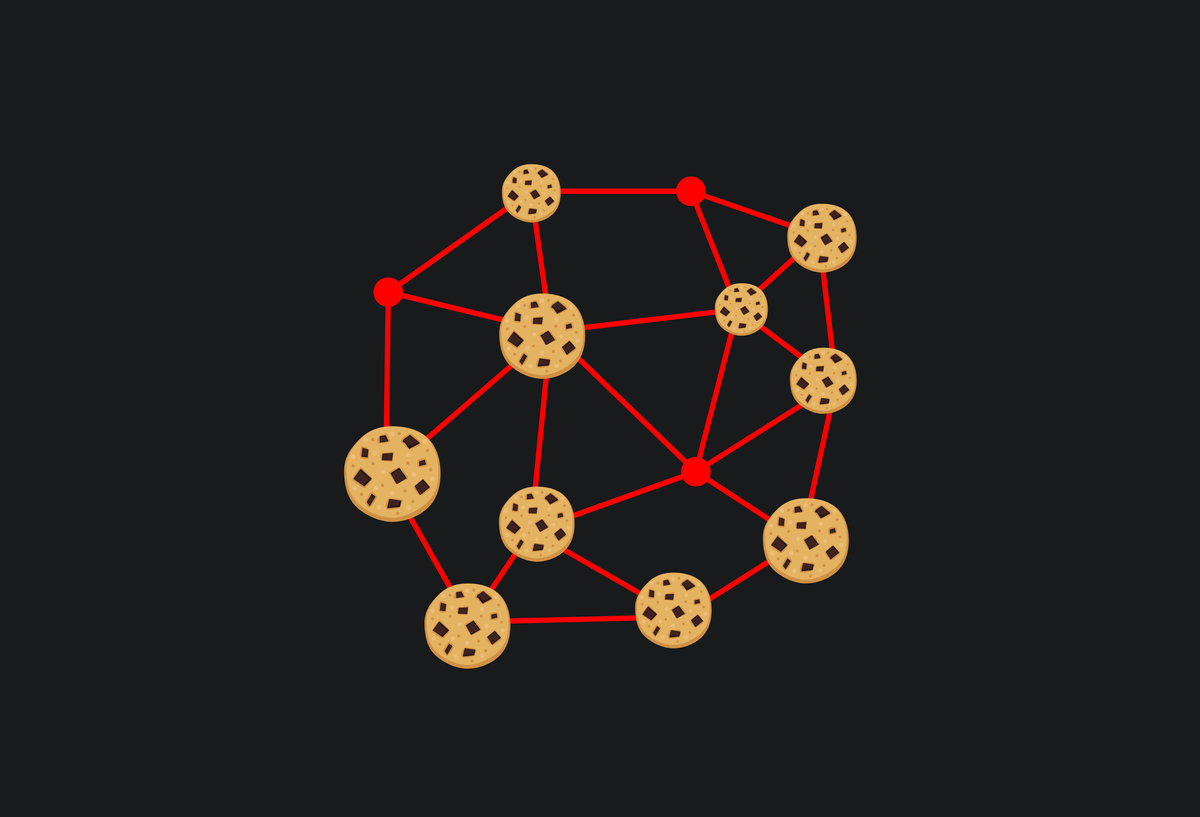
งานอดิเรกอย่างนึงของผมคือการนั่งอ่าน paper ที่เขาวิจัยอะไรแปลก ๆ เอาจริงคอนเทนต์จำนวนมากที่ผมเขียนลงเพจก็มางานอดิเรกนี้ของผมนั่นแหละ และคอนเทนต์นี้ก็เช่นกัน

ผมไปเจองานวิจัยชิ้นหนึ่งชื่อว่า A topological analysis of the space of recipes หรือถอดความเป็นภาษาไทยได้ประมาณว่า การวิเคราะห์ปริภูมิสูตรอาหารเชิงโทโพโลจี ซึ่งฟังดูอีหยังวะสุด ๆ

คือถ้าคุณเรียนคณิตศาสตร์ไปถึงจุดนึงคุณจะรู้จัก space เยอะมาก มันถูกใช้ในความหมายของเซตที่เก็บรวบรวมอะไรสักอย่างอยู่พร้อมกับโครงสร้างบางอย่าง เช่น vector space ในวิชา Linear Algebra ที่หมายถึงเซตของเวกเตอร์และโครงสร้างของมัน หรือ sample space ในวิชาความน่าจะเป็น ที่หมายถึงเซตของตัวอย่างและโครงสร้างของมัน แล้วก็มี space นั่น space นี่เยอะแยะไปหมด ขึ้นอยู่กับว่าเราสนใจเซตและโครงสร้างของอะไร แต่ผมไม่เคยได้ยินคำว่า space ของสูตรอาหารมาก่อน

ส่วนคำว่า topological analysis นั้น โดยปกติแล้วมันหมายถึงการวิเคราะห์สมบัติเชิงสัณฐานของอะไรสักอย่าง โดยเฉพาะสมบัติที่ไม่เปลี่ยนแปลงไปด้วยการยืดหรือบิด เช่นการวิเคราะห์ว่ามันมีกี่รู เหมือนที่เราสามารถมองว่าแก้วกาแฟกับขนมโดนัทนั้นเหมือนกันเพราะว่ามันมีหนึ่งรู ส่วนกางเกงนั้นไม่เหมือนเพราะว่ามีสองรูนั่นแหละฮะ

ดังนั้นคำว่า A topological analysis of the space of recipes จึงไม่มีความหมายอะไรสำหรับผมเลย space ของสูตรอาหารคืออะไร และเราจะไปวิเคราะห์สมบัติเชิงสัณฐานอะไรของมัน ความสงสัยทั้งหมดนี้เองที่ทำให้ผมเริ่มต้นอ่าน paper นี้

สิ่งนี้เขาทำคืออย่างนี้ฮะ ขั้นแรก เขาไปเปิดตำราอาหาร แล้วนับว่าถ้าเราเอาวัตถุดิบที่ใช้จากทุกสูตรมารวมกันเนี่ย มันจะมีอะไรบ้าง เพื่อความง่ายผมจะสมมติว่าตำราอาหารของเรามีสูตรอาหารอยู่ 5 สูตร และจากทั้ง 5 สูตรนี้มีวัตถุดิบที่ใช้ทั้งหมด 4 อย่าง

สร้างออกมาเป็นเวกเตอร์ขนาด 4 มิติจำนวน 5 เวกเตอร์ แต่ละเวกเตอร์แทนหนึ่งสูตรอาหาร และแต่ละตำแหน่งจะเป็นตัวบอกว่าในสูตรนั้น ๆ ใส่วัตถุดิบนั้นหรือเปล่า ใครที่ตามไม่ทันลองดูรูปข้างล่างประกอบ

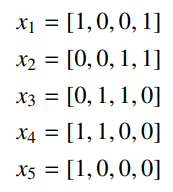
0 แปลว่าไม่ใส่ 1 แปลว่าใส่ อย่างสูตรที่ 1 นั้น ใส่วัตถุดิบที่ 1 กับ 2 ในขณะที่สูตรที่ 2 นั้นใส่วัตถุดิบที่ 3 และ 4 ไล่ไปแบบนี้เรื่อย ๆ

ทีนี้พอเราได้เวกเตอร์ปุ๊บ เราก็จะเอาเวกเตอร์พวกนั้นมาคำนวณหาค่าความแตกต่าง เพื่อบอกว่าในบรรดาสูตรอาหารทั้งหมดที่เรามี สูตรไหนคล้ายกัน สูตรไหนแตกต่างกัน ได้ผลออกมาตามรูปข้างล่าง

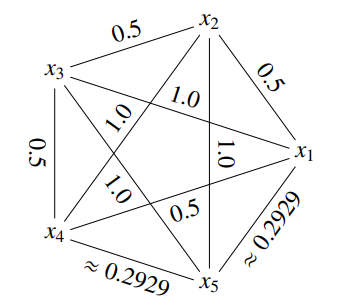
จากนั้นครับ เราจะต้องกำหนดเกณฑ์ขึ้นมา เกณฑ์ที่เอาไว้ใช้แบ่งว่า ต้องต่างกันเกินเท่าไรถึงจะเรียกว่าสองสูตรนี้ไม่คล้ายกันแล้ว โดยเราจะเริ่มต้นจากการใช้เกณฑ์คือ 0 ซึ่งแปลว่าไม่มีใครคล้ายกันเลย แล้วค่อย ๆ เพิ่มเกณฑ์นี้ทีละนิด

ถ้าดูจากแผนภาพด้านบนจะเห็นว่าถ้าเราใช้เกณฑ์คือ 0.2 จะพบว่าไม่มีใครคล้ายกันเลยอยู่ดี แต่ถ้าเราขยับเกณฑ์ขึ้นไปถึง 0.3 จะได้ว่าสูตรที่ 4 และ 5 กับสูตรที่ 1 และ 5 จะถูกมองว่าคล้ายกันแล้ว พอมันคล้ายกันปุ๊บ เราก็ลากเส้นเชื่อมระหว่างมัน

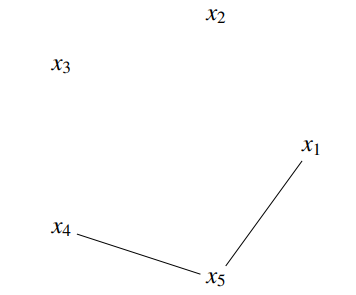
กระบวนการนี้เรียกว่าการสร้าง Vietoris–Rips complex เพื่อค่อย ๆ ดูโครงสร้างว่ามีโครงสร้างอะไรเกิดขึ้นบ้างเมื่อเราใช้เกณฑ์ต่าง ๆ กันไป ซึ่งจะเห็นว่าเมื่อเราเพิ่มเกณฑ์ขึ้นไปถึงจุดนึง เส้นเชื่อมเหล่านี้มันจะเริ่มฟอร์มตัวเป็นวงปิดขึ้นมา และการวิเคราะห์วงปิดที่อยู่นาน ๆ ที่เรียกกันว่า Persistent Homology นี้แหละที่แสดงว่าเวกเตอร์ที่เราสนใจนั้นอาจจะวางอยู่บน space ที่มีสัณฐานที่มีรูก็ได้

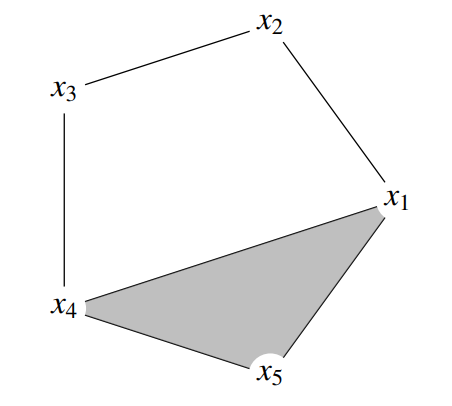
ผู้วิจัยเสนอว่า การที่มันเกิดรู แปลว่ามันยังมีช่องโหว่ใน space ของสูตรอาหาร ดังนั้นถ้าเราหารูพวกนั้นเจอ แล้วเสนอสูตรอาหารที่ควรจะอยู่ตรงรูนั้น เราควรจะได้สูตรอาหารที่อร่อย และไม่เคยมีมาก่อนในโลกนี้

โห คิดได้ไงอ่ะ

เพื่อทดสอบไอเดียนี้ พวกเขาจึงลองไปรวบรวมสูตรการทำบิสกิตมา 19 สูตร แล้วเอามาทำกระบวนการทั้งหมดที่ผมได้อธิบายไป คือเปลี่ยนแต่ละสูตรเป็นเวกเตอร์ สร้างกราฟ หารู และเสนอสูตรการทำบิสกิตใหม่จากรูที่ได้พวกนั้น พวกเขาเสนอสูตรบิสกิตแบบใหม่ถึง 4 สูตร ที่ไม่ซ้ำกับทั้ง 19 สูตรที่หามา ก่อนจะเอาไปให้คนทั่วไปชิมแบบ blind test แล้วบอกว่าสูตรที่พวกเขาคิดขึ้นนั้นรสชาติเป็นยังไงบ้างเมื่อเทียบกับสูตรมาตรฐาน

ก่อนจะไปถึงตรงนั้น ผมเอารูปมาให้ดูก่อน อันซ้ายสุดคือสูตรมาตรฐาน ส่วนที่เหลือคืออันที่คิดค้นขึ้นมาใหม่ด้วยคณิตศาสตร์

และผลที่ได้คือไม่ต่าง ที่แปลว่า ผู้ร่วมทดลองไม่ได้รู้สึกว่าอันไหนอร่อยกว่าอันไหนมากเป็นพิเศษ มองในมุมนึงก็คือสูตรใหม่ที่คิดขึ้นมาได้นั้นก็ไม่ได้อร่อยไปกว่าสูตรเดิมที่มีอยู่แล้วหรอก แต่อย่าลืมว่าจุดตั้งต้นของงานวิจัยนี้เขาไม่ได้ต้องการสร้างสูตรอาหรที่อร่อยขึ้น เขาแค่ต้องการสร้างสูตรที่ใหม่ อย่าลืมว่าสูตรบิสกิตใหม่ ๆ พวกนี้นั้นไม่ได้คิดโดยคน แต่มาจากการใช้กระบวนการทางโทโพโลจีสร้างมา ซึ่งสำหรับผม แค่มันกินได้และไม่ได้ถูกตัดสินว่ารสชาติห่วยแตกก็โคตรจะเจ๋งแล้ว

ความจริงแล้วการพยายามเข้าใจโครงสร้างของสูตรอาหารนั้นไม่ใช่เรื่องใหม่ นักวิทยาศาสตร์และนักปรุงอาหารเขาก็ศึกษาและทดลองจับคู่รสชาติให้ลงตัวมาตั้งนานแล้ว และด้วยความก้าวหน้าของเทคโนโลยี เราจึงสามารถใช้เครื่องมือทางคณิตศาสตร์เพื่อทำความเข้าใจโครงสร้างของสูตรอาหาร และค้นพบรูปแบบที่อาจจะไม่เคยเห็นมาก่อน ซึ่งไม่เพียงแค่ช่วยให้เราเข้าใจสูตรอาหารที่มีอยู่ลึกซึ้งขึ้น แต่ยังเปิดโอกาสในการสร้างสูตรอาหารใหม่ ๆ ที่อาจจะเป็นที่นิยมในอนาคตก็ได้

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง
https://arxiv.org/pdf/2406.09445v1
https://towardsdatascience.com/topological-data-analysis-tda-b7f9b770c951/
https://www.frontiersin.org/journals/artificial-intelligence/articles/10.3389/frai.2021.667963/full
https://www.nature.com/articles/srep00196