สามเหลี่ยมมุมฉากด้านเท่า รูปสองเหลี่ยม และโลกที่ไม่มีเส้นขนาน

เคยได้ยินคำว่า "สามเหลี่ยมมุมฉากด้านเท่า" ไหมฮะ

ไม่น่าเคย ถ้าเคยสิแปลก เพราะสามเหลี่ยมุมฉากคือสามเหลี่ยมที่มีมุมฉากอยู่ 1 มุม ส่วนสามเหลี่ยมด้านเท่าคือสามเหลี่ยมที่ทุกด้านยาวเท่ากัน ดังนั้นสามเหลี่ยมมุมฉากด้านเท่าแปลว่ามันต้องมีมุมฉาก และทุกด้านก็ต้องยาวเท่ากันด้วย ซึ่งถ้านึกตามดี ๆ ด้วยความรู้เรขาคณิตพื้นฐานจะพบว่ามันเป็นไปไม่ได้ เพราะสามเหลี่ยมด้านเท่าจะมีมุมทุกมุมเท่ากับ 60 องศาเสมอ ดังนั้นมันจะไม่มีทางเป็นสามเหลี่ยมมุมฉากได้

หรือมองในอีกแง่ ด้วยความรู้ที่ว่ามุมภายในของรูปสามเหลี่ยมจะเท่ากับ 180 องศาเสมอ ถ้ามุมนึงมันฉากไปแล้ว ก็คือหักไป 90 เราจะไม่สามารถมีมุมฉากอีกมุมได้ ไม่งั้นบวกกันมันจะเกิน 180 ถูกไหมฮะ จะมองยังไงรูปสามเหลี่ยมมุมฉากด้านเท่าก็เป็นรูปที่สร้างขึ้นจริงไม่ได้

แต่ถ้าผมบอกว่าจริง ๆ แล้วมันเกิดขึ้นได้ล่ะ

จินตนาการว่าคุณยืนอยู่ที่ขั้วโลกเหนือ คุณเริ่มออกเดินไปตามแนวเส้นลองจิจูดสักเส้นไปเรื่อย ๆ สักพักนึงคุณจะเดินมาถึงเส้นศูนย์สูตร ถึงตอนนั้นคุณเลี้ยวขวาทำมุมฉากกับทางที่เดินมา แล้วเริ่มเดินต่อไปเรื่อย ๆ บนเส้นศูนย์สูตร จนผ่านไป 1/4 ของโลก จากนั้นเลี้ยวขวาอีกที เดินไปเรื่อย ๆ และคุณจะพบว่าตัวเองจะกลับไปโผล่ที่ขั้วโลกเหนืออีกครั้ง จุดเดียวกับที่คุณเริ่มเดินเป๊ะเลย ใครที่นึกภาพตามไม่ทัน ดูรูปข้างล่างนี้ประกอบไปด้วยก็ได้ฮะ

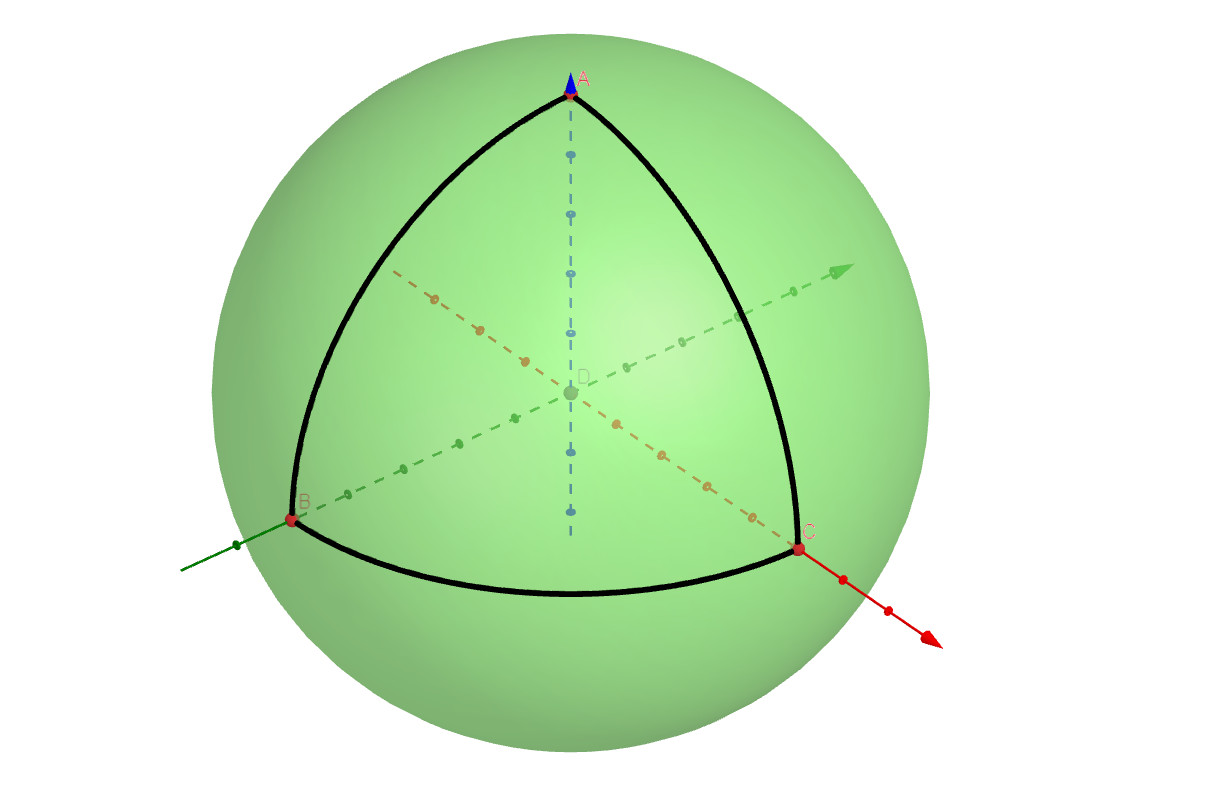
นี่ไงฮะ ทุกด้านยาวเท่ากัน คือเท่ากับ 1/4 ของเส้นรอบวงโลก และทุกมุมเป็นมุมฉาก เป็นสามเหลี่ยมมุมฉากด้านเท่าตามที่เราต้องการ

ระบบเรขาคณิตที่เราเรียนกันในระดับประถมมัธยมนั้นเรียกว่าเรขาคณิตระบบยูคลิด ซึ่งว่าด้วยรูปทรงต่าง ๆ บนระนาบ ซึ่งเรขาคณิตในระบบนี้นั้นก็มีกฎหรือทฤษฎีต่าง ๆ ตามที่เราเรียนกันในห้องเรียนนั่นแหละ ไม่ว่าจะเป็นสมบัติที่ว่ามุมภายในของรูปสามเหลี่ยมจะเท่ากับ 180 องศาเสมอ ทฤษฎีบทพิทากอรัส หรือพวกเอกลักษณ์ตรีโกณมิติต่าง ๆ

แต่กฎพวกนี้นั้นไม่ได้จริงเสมอไปในเรขาคณิตบนรูปทรงอื่น ที่เห็นกันชัด ๆ ก็คือการมีอยู่ของสามเหลี่ยมมุมฉากด้านเท่าที่เกิดไม่ได้ในเรขาคณิตแบบยูคลิด แต่สามารถเกิดขึ้นได้ในเรขาคณิตบนผิวทรงกลม ซึ่งความจริงแล้วเรขาคณิตบนผิวทรงกลมนั้นมีสมบัติประหลาด ๆ อีกหลายอย่าง แต่อันที่ผมอยากยกมาเล่าให้ฟังอีกอันคือเรื่องรูปสองเหลี่ยม

รูปสองเหลี่ยมฟังดูไม่มีความหมายสุด ๆ ในเรขาคณิตแบบยูคลิด เพราะลำพังเส้นตรงสองเส้นมันจะมาประกอบกันเป็นรูปได้ยังไง แต่รูปสองเหลี่ยมนั้นปกติมากในเรขาคณิตบนผิวทรงกลม แค่คุณเดินจากขั้วโลกเหนือมาขั้วโลกใต้บนแนวเส้นลองจิจูดสักเส้น แล้วเดินกลับไปขั้วโลกเหนือตามแนวเส้นลองจิจูดอีกเส้นหนึ่ง นั่นก็คือรูปสองเหลี่ยมแล้วถูกไหมฮะ

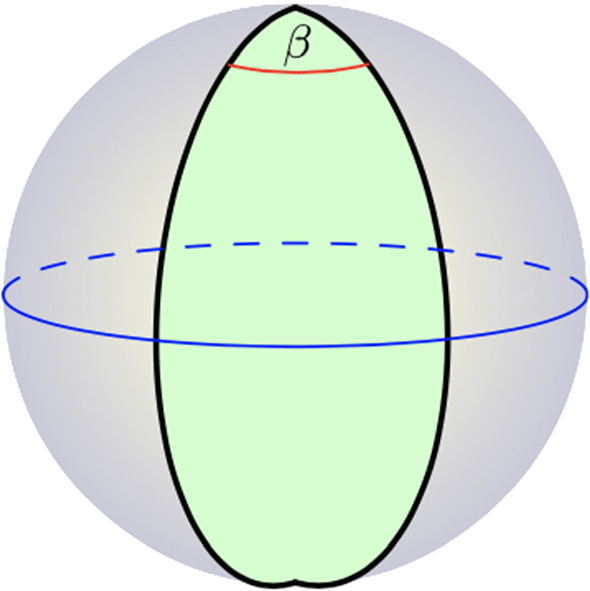
สมบัติข้อหนึ่งที่พื้นฐานมาก ๆ ในเรขาคณิตแบบยูคลิดคือการมีอยู่ของเส้นขนาน คือถ้าเรามีเส้นตรงอยู่เส้นหนึ่ง เราจะหาเส้นอีกเส้นที่ไม่ตัดกับมันได้เสมอ แต่สมบัตินี้ไม่จริงในเรขาคณิตบนผิวทรงกลม เพราะเส้นตรงบนผิวทรงกลมคือวงกลมใหญ่ที่ลากรอบวงกลม ซึ่งเส้นพวกนี้จะไปตัดกันเสมอ นึกถึงเส้นลองจิจูดที่ไปตัดกันที่ตรงขั้วโลกก็ได้

ฟังแบบนี้คุณอาจจะเริ่มคิดว่า ไม่เห็นจริงเลย ลองนึกถึงเส้นละติจูดสิ เส้นละติจูดหรือเส้นที่ลากในแนวนอนขนานไปกับเส้นศูนย์สูตร เส้นพวกนั้นก็ไม่เห็นจะตัดกันสักเส้นเลย ไหนบอกว่าไม่มีเส้นขนานไง ก็ต้องบอกว่า คิดแบบนั้นไม่ได้ฮะ เพราะเส้นละติจูดพวกนั้นไม่นับว่าเป็นเส้นตรงบนผิวโลก เพราะจริง ๆ แล้วมันไม่ได้ตรง

เวลาเราพูดว่าเส้นไหนเป็นเส้นตรงนั้น เรากำลังหมายความว่ามันคือเส้นทางที่สั้นที่สุดที่ลากจากจุดหนึ่งไปอีกจุดหนึ่ง ซึ่งการเดินทางตามเส้นละติจูดนั้นไม่ใช่วิธีเดินทางที่สั้นที่สุด นี่จึงเป็นเหตุผลที่เวลาดูแผนที่การบินเราถึงรู้สึกว่าเครื่องบินมันไม่บินเป็นเส้นตรง ทั้งที่จริง ๆ แล้วมันบินเป็นเส้นตรง แต่เป็นเส้นตรงบนผิวโลก ไม่ใช่ตรงบนแผนที่ที่คลี่ทรงกลมออกมา

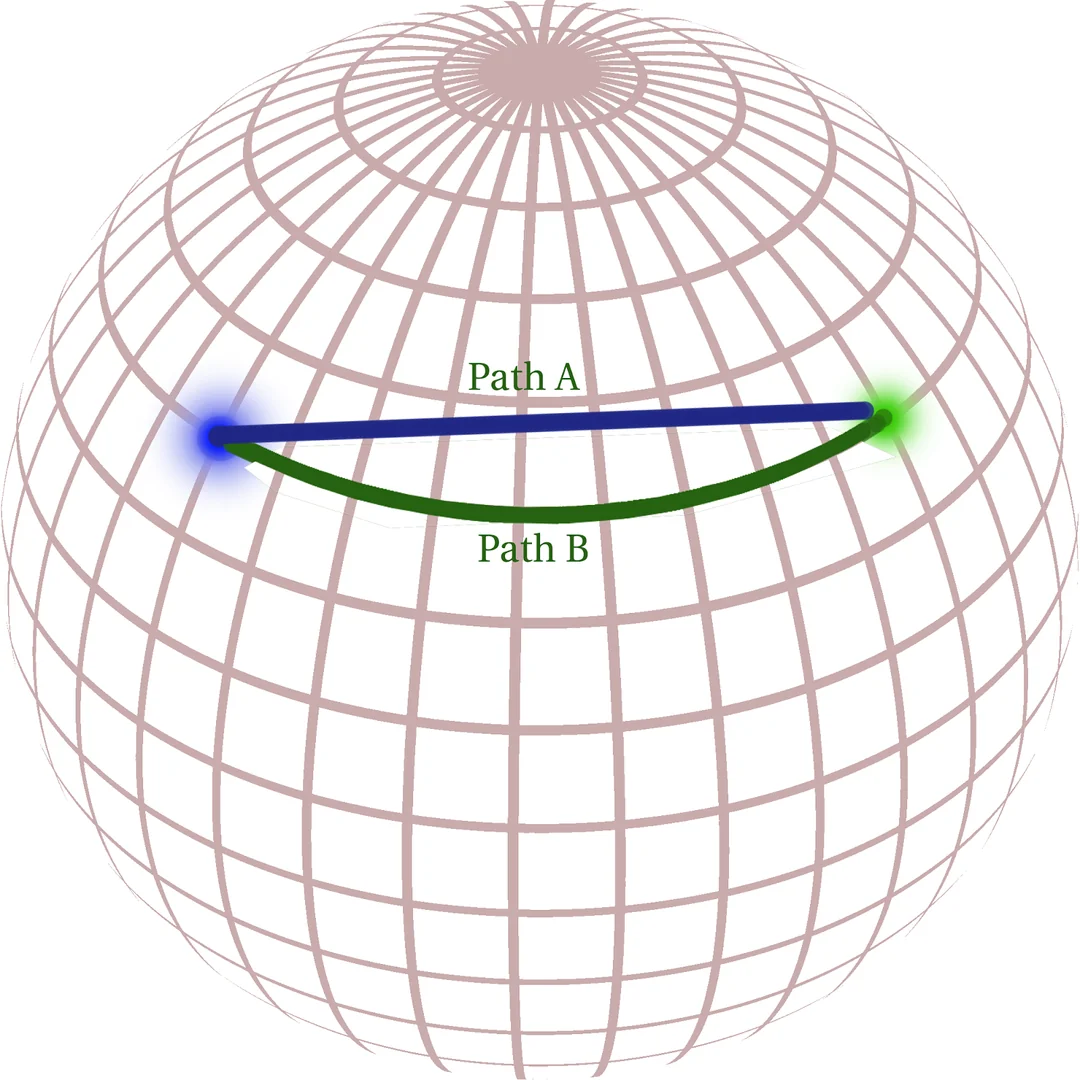
ดังนั้นเราจึงสรุปได้ว่า เส้นตรงทุกเส้นในเรขาคณิตบนผิวทรงกลมนั้นจะตัดกันเสมอ ดังนั้นการพูดถึงเส้นขนานจึงไม่มีความหมายในเรขาคณิตระบบนี้

ความจริงผมเคยเขียนเรื่องทำไมเครื่องบินถึงไม่บินเป็นเส้นตรงไปแล้วช่วงเปิดเพจใหม่ ๆ ใครที่ยังไม่เคยอ่านแวะไปอ่านได้ตามลิงก์นี้เลยนะฮะ https://shorturl.at/3rkI0

นอกจากเรขาคณิตบนผิวทรงกลมแล้ว เรายังมีเรขาคณิตระบบอื่น ๆ ที่ไม่ใช่ยูคลิดอยู่อีกมากมาย ความจริงแล้วเรขาคณิตที่ไม่ใช่แบบยูคลิดนั้นแบ่งได้เป็นสองกลุ่มหลัก คือกลุ่ม hyperbolic และกลุ่ม elliptic ซึ่งผิวทรงกลมนับเป็นเรขาคณิตแบบ elliptic ชนิดหนึ่ง

ในขณะที่มุมภายในของสามเหลี่ยมในเรขาคณิตแบบยูคลิดนั้นเท่ากับ 180 องศาเสมอ มุมภายในของสามเหลี่ยมในเรขาคณิตแบบ elliptic จะมากกว่า 180 องศาเสมอ นั่นจึงเป็นสาเหตุที่เราสามารถสร้างสามเหลี่ยมมุมฉากด้านเท่าได้ ส่วนในเรขาคณิตแบบ hyperbolic มุมภายในของสามเหลี่ยมจะน้อยกว่า 180 องศาเสมอ

แม้ว่าโลกของเราจะไม่ได้เป็นทรงกลมเป๊ะ ๆ แต่การเข้าใจเรขาคณิตแบบ elliptic ก็มีประโยชน์อย่างมากในการเดินเรือ ระบบนำทางเครื่องบิน การทำแผนที่ การระบุตำแหน่งทางภูมิศาสตร์ และอื่น ๆ อีกมากมาย การเข้าใจการโค้งของโลกช่วยให้การคำนวณระยะทางและทิศทางมีความแม่นยำมากขึ้น นอกจากนี้เรขาคณิตแบบ elliptic ถูกนำมาใช้ในงานวิจัยด้านวิศวกรรม เช่น การออกแบบโครงสร้างที่มีลักษณะโค้ง เช่น โดมและสะพาน ซึ่งการใช้รูปทรงโค้งแบบ elliptic สามารถช่วยเพิ่มความแข็งแรงและประสิทธิภาพในการกระจายน้ำหนัก ส่วนเรขาคณิตแบบ hyperbolic นั้นก็มีบทบาทสำคัญในหลายๆ ด้าน เช่น ในทางฟิสิกส์การศึกษาการเคลื่อนที่ของวัตถุในพื้นที่ที่มีแรงโน้มถ่วงสูงหรืออวกาศที่มีลักษณะโค้งแปลก ๆ อีกด้วย

ในฐานะมนุษย์ตัวเล็ก ๆ บนผิวโลก การเรียนเรขาคณิตแค่แบบยูคลิดนั้นอาจจะพอแล้วแหละ เพราะสุดท้ายแล้วความโค้งของผิวโลกนั้นก็เล็กน้อยมาก ๆ จนมนุษย์อย่างเรารับรู้ถึงมันไม่ได้ด้วยซ้ำ แต่เมื่อเราเริ่มอยากเดินทางข้ามโลก หรือเข้าใจองค์ประกอบต่าง ๆ ที่ไกลออกไปในจักรวาล การเข้าใจเรขาคณิตในระบบที่แตกต่างออกไปก็เป็นเรื่องสำคัญ

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง
https://mathworld.wolfram.com/SphericalLune.html
https://brilliant.org/wiki/spherical-geometry/
https://cmc.deusto.eus/introduction-to-spherical-geometry-postulates-and-pythagoras-theorem/
https://forum.gcaptain.com/t/in-spherical-geometry-there-are-no-parallel-lines/71463
https://www.vaia.com/en-us/explanations/math/geometry/spherical-geometry/