แคลคูลัสที่ไม่มีดิฟ ที่แปลว่า ถึงอยากดิฟก็ดิฟไม่ได้

เมื่อวานผมลง meme อันนึงในเพจไปแล้วแพร่มว่าอยากเขียนเรื่อง subderivative แต่กลัวไม่มีคนอ่าน ปรากฎว่าคนคอมเมนต์ว่าสนใจอ่านกันมาเพียบเลย โอเคฮะ จัดไป

ผมเริ่มแบบนี้ฮะ คือในวิชาแคลคูลัสเนี่ย เรานิยามให้ดิฟหรืออนุพันธ์ของฟังก์ชัน f ที่จุด x ให้เป็น

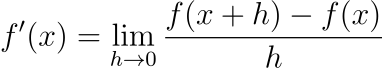
เมื่อลิมิตมีค่า โดยไอ้คำว่าเมื่อลิมิตมีค่าเนี่ยมักจะถูกละเลยไป เพราะส่วนใหญ่ฟังก์ชันที่เราสนใจในวิชาแคลคูลัสนั้นเราสามารถหาค่าเจ้าลิมิตตัวนี้ได้เสมอ แต่ในความจริงแล้วมันมีฟังก์ชันที่หาลิมิตที่ว่านี่ไม่ได้บางจุดอยู่ เช่นฟังก์ชัน f(x)=|x| เนี่ย เราจะพบว่าลิมิตทางซ้ายและลิมิตทางขวาของนิยามดิฟนั้นมีค่าไม่เท่ากัน ซึ่งเราเรียกว่าที่จุดนั้นมันหาอนุพันธ์ไม่ได้

ทีนี้ การที่ฟังก์ชันหาอนุพันธ์ไม่ได้นั้นส่งผลเสียยังไง โห เยอะเลยฮะ โดยเฉพาะอย่างยิ่งในปัญหาการหาค่าต่ำสุด ซึ่งปกติเราจะใช้การดิฟแล้วจับเท่ากับศูนย์กัน เช่นถ้าอยากหาค่าต่ำาุดของฟังก์ชัน f(x)=x^2 เราก็ดิฟมัน ได้ f'(x)=2x จับเท่ากับศูนย์ แก้สมการได้ x=0 เป็นจุดต่ำสุด แต่พอเป็น f(x)=|x| ซึ่งหาอนุพันธ์ไม่ได้ แล้วจุดต่ำสุดก็ดันไปอยู่ตรงที่หาอนุพันธ์ไม่ได้ซะด้วย ก็มีปัญหาเลย

หรือไปให้ไกลกว่านั้น เวลาเราทำ least square regression เพื่อหาเส้นตรงที่ดีที่สุด เราพยายาม minimize ค่า sum square error ถูกไหมฮะ ซึ่งเรา square มันเพื่อให้มันเป็นบวก ตอนนั้นมีใครเคยสงสัยไหมว่าทำไมเราถึงเลือกที่จะกำลังสอง แทนที่จะใส่ค่าสัมบูรณ์ คำตอบง่าย ๆ ก็คือเพราะการยกกำลังสองนั้นมันดิฟได้ พอดิฟได้เราก็สามารถหา minimize มันได้ ไม่ว่าจะต้องการดิฟตรง ๆ แล้วจัดรูป หรือแม้จะไปใช้พวกวิธีเชิงตัวเลขอย่าง gradient descent สุดท้ายเราก็ต้องดิฟอยู่ดี

แต่คิดว่านักคณิตศาสตร์จะยอมจำนนต่อการดิฟไม่ได้ลงง่าย ๆ แค่นั้นหรอฮะ ไม่มีทางเสียหรอก ดิฟไม่ได้ก็ไม่ดิฟ แต่ไปทำอย่างอื่นที่ general กว่าดิฟแทนสิ จึงเกิดเป็นคอนเซ็ปที่เรียกว่า subderivative ขึ้นมาฮะ

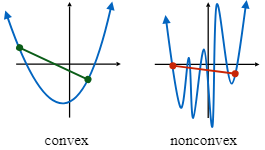
เพื่อความง่าย เราจะเริ่มจากฟังก์ชันที่มีสมบัติ convex นั้นคือห้อยลงมาข้างล่างก่อน คือปกติแล้วเรานิยาม derivative ว่าเป็นความชันของเส้นตรงที่ 'สัมผัส' กับฟังก์ชันที่จุดนั้น ๆ ถูกไหมฮะ แต่สำหรับ subderivative เรานิยามให้เป็นความชันของเส้นตรงที่ 'สัมผัสอยู่ข้างใต้' ฟังก์ชันที่จุดนั้น ๆ ฮะ ซึ่งจะเห็นว่าสำหรับฟังก์ชัน f(x)=|x| นั้น เราสามารถหาเส้นตรงมาสัมผัสอยู่ข้างใต้ฟังก์ชันของเราที่จุด 0 ได้เยอะไปหมดเลย

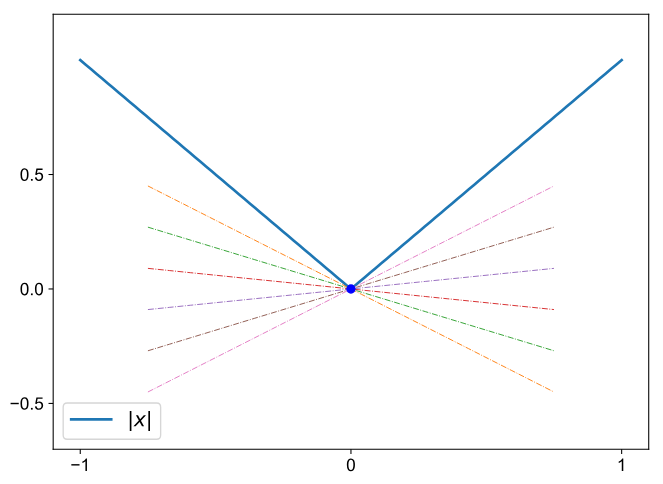
จากรูปจากเห็นว่า เส้นตรง y=ax ที่ a ตั้งแต่ -1 ถึง 1 นั้นล้วนแต่สัมผัสอยู่ข้างใต้ฟังก์ชัน f(x)=|x| ดังนั้นถ้าเรานิยามให้ subderivative คือความชันของเส้นตรงที่สัมผัสอยู่ข้างใต้ฟังก์ชันที่จุดนั้น แปลว่า subderivative ของฟังก์ชัน f(x)=|x| ที่จุด 0 นั้นคือค่าอะไรก็ได้ในช่วงปิด [-1,1]

ใช่ฮะ subderivative ที่แต่ละจุดจะออกมาเป็นเซต ไม่ได้ออกมาเป็นค่าค่าเดียวแบบตอนเราดิฟธรรมดา ซึ่งถ้าใครที่พอเก็ตนิยามแล้วก็น่าจะเห็นว่า ถ้าที่จุดนั้นฟังก์ชันหาอนุพันธ์ได้ เราจะได้ว่า subderivative ของมันจะเป็นเซตที่มีสมาชิกแค่ตัวเดียว หรือก็คือออกมาเป็นค่าค่าเดียวนั่นแหละ สรุปคือ เราได้ว่า subderivative ของ f(x)=|x| คือ

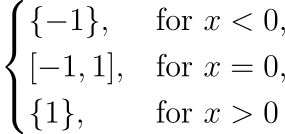
ก็คือไม่ได้ออกมาเป็นค่า แต่ออกมาเป็นเซตนั่นเอง

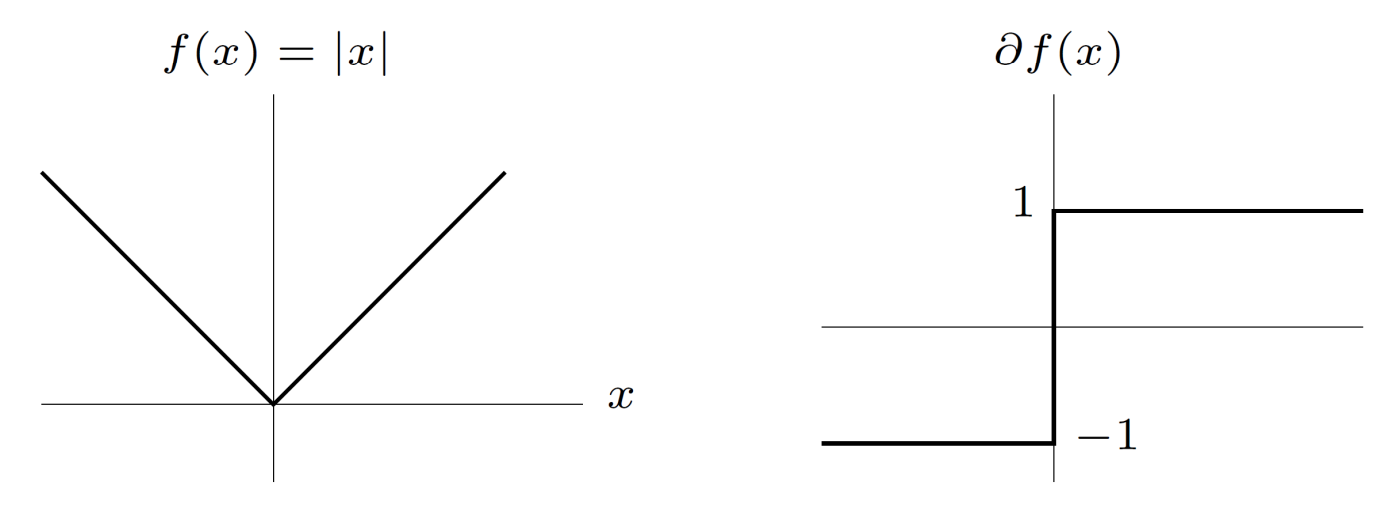
ความเจ๋งของ subderivative ก็คือ สำหรับฟังก์ชันของจำนวนจริงที่ convex เราจะได้ว่า subderivative จะมีค่าเสมอทุกจุด ต่างจากดิฟปกติที่มีค่าบ้างไม่มีบ้าง และแน่นอนว่าสมบัติต่าง ๆ ที่เราเรียนในแคลคูลัสเกี่ยวกับดิฟเช่นการกระจายการบวก กฎผลคูณ กฎลูกโซ่ ก็มีบางอันที่ยังจริงสำหรับ subderivative แต่บางอันก็ยังจริงเฉพาะบนเงื่อนไขบางอย่าง ซึ่งผมจะไม่ลงรายละเอียดตรงนี้ แต่แปะ link สำหรับอ่านเพิ่มไว้ตอนท้ายแล้ว

แต่ที่อยากชวนดูนิดเดียวนิดเดียวคือ อย่าลืมว่าสมบัติง่าย ๆ อย่างเช่นการกระจายการบวกที่เราเคยมีว่า (f+g)'(x) = f'(x)+g'(x) นั้น พอมันกลายเป็น subderivative แล้วการบวกก็ต้องไม่ใช่การบวกปกติแล้ว เพราะคราวนี้เราไม่ได้เอาตัวเลขบวกกัน แต่เอาเซตบวกกันแทน

ส่วนสมบัติที่สำคัญที่สุดเกี่ยวกับดิฟที่บอกว่า ถ้าฟังก์ชันดิฟได้ ดิฟที่จุดต่ำสุดของฟังก์ชันที่ convex จะมีค่าเป็นศูนย์เสมอ เราก็สามารถขยายมันออกมาได้เป็นสมบัติใหม่ที่ว่า subderivative ที่จุดต่ำสุดของฟังก์ชันที่ convex จะมีค่าเป็นศูนย์เป็นสมาชิกอยู่ในนั้นเสมอ แทน

การนิยาม subderivative อนุญาตให้เรามีวิธีการหาค่าต่ำสุดของฟังก์ชันอย่างเช่น Subgradient Method ซึ่งคือเวอร์ชันอัพเกรดของ Gradient Descent Method แต่ที่เขาไม่เอาคำว่า Descent มาใส่แล้ว เพราะพอเราไปใช้ subgradient แทน ค่าของฟังก์ชันอาจจะไม่ได้น้อยลงตลอดเวลา มีเพิ่ม ๆ ลด ๆ แกว่งบ้าง

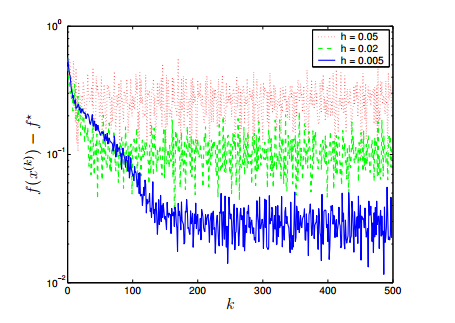
ฟังก์ชันที่ดิฟไม่ได้แบบนี้บางทีเราก็เรียกว่าฟังก์ชันที่ nonsmooth ฮะ คือมันหักไปหักมา ดังนั้นมันจึงมีวิชาที่ชื่อ nonsmooth analysis ซึ่งมุ่งศึกษาแคลคูลัสของฟังก์ชันแบบนั้นโดยเฉพาะเลย รวมไปถึงศาสตร์ต่าง ๆ ที่เอาความรู้พวกนี้ไปประยุกต์ใช้ ใครสนใจก็ลองไปค้นต่อได้ ผมทิ้ง keyword ไว้บ้างแล้ว กับเดี๋ยวจะแปะ link ที่ผมเห็นว่าอ่านไม่ยากมาก (แต่ก็ยังน่าจะยากไปเยอะเลยสำหรับคน non-math)

ประมาณนี้แล้วกันฮะ

และเช่นเดิม ใครที่อยากช่วยสนับสนุนเพจเว็บไซต์ของเราให้ผลิตคอนเทนต์คณิตศาสตร์ที่ไม่น่าจะมีคนยอมจ้างให้ไปเขียนลงที่ไหนอย่างนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

แหล่งอ้างอิง
https://www.damtp.cam.ac.uk/user/hf323/L22-III-OPT/lecture5.pdf
https://stanford.edu/class/ee364b/lectures/subgradients_notes.pdf
http://faculty.bicmr.pku.edu.cn/~wenzw/opt2015/lect-sg.pdf
https://optimization.cbe.cornell.edu/index.php?title=Subgradient_optimization
https://arxiv.org/pdf/2001.00216