เราทำให้เกม this or that จบเร็วกว่านี้ได้ไหม

ใครชอบดูพวกคลิป TikTok หรือ Reel น่าจะเคยเห็นคลิปที่เขาเล่น This or That กันอยู่บ้าง ที่เขาจะถามว่า ระหว่างอันนี้กับอันนั้นเลือกอะไร เหลือคำตอบสุดท้ายที่เขาชอบที่สุด สารภาพว่าตอนแรกผมก็ดูโดยไม่ได้คิดอะไรฮะ จนพอมันเห็นผ่านตาบ่อย ๆ เข้า ก็เริ่มตั้งคำถามทางคณิตศาสตร์เกี่ยวกับมันขึ้นมา
เผื่อใครไม่เคยดู ขอเล่าให้ฟังหน่อย ในคลิปจะมีคนโดนถามว่า "ชอบอันนี้หรืออันนั้น?" สมมุติว่าเค้าถามว่า “ชอบกินแอปเปิ้ลหรือมะละกอ?” แล้วคนถูกถามตอบว่า “แอปเปิ้ล” ทีนี้แอปเปิ้ลก็จะได้ไปต่อ จากนั้นก็ถามอีกว่า “แอปเปิ้ลหรือกล้วย?” ถ้าเลือกกล้วย กล้วยก็ไปต่อแทน ไล่แบบนี้ไปเรื่อย ๆ พอถามจนครบก็จะรู้แล้วว่า อันสุดท้ายที่เหลือคือสิ่งที่ชอบที่สุด
คำถามคือ การหาของที่ชอบที่สุดด้วยการให้เลือกไปเรื่อย ๆ ทีละคู่แบบนี้มันมีประสิทธิภาพจริงหรือเปล่า หรือจริง ๆ แล้วเรามีวิธีที่ดีกว่าในการหาของที่ชอบที่สุด
ถ้ามองง่าย ๆ ขั้นตอนวิธีที่มีประสิทธิภาพคือขั้นตอนวิธีที่ใช้เวลาไม่นาน ลองนึกภาพว่าเราไปถึงจุดหมายเดียวกันแต่ทางนึงใช้เวลาเป็นชั่วโมง อีกทางนึงใช้เวลาแค่ 15 นาที อันหลังก็ย่อมดีกว่า ในกรณีของ this or that เราสามารถมองได้ว่าเวลาในการหาของที่ชอบที่สุดก็คือจำนวนคำถามที่ต้องถามนั่นเอง
ทีนี้ สมมติว่าเรามีผลไม้ในลิสต์อยู่ 4 ชนิด คือ แอปเปิ้ล มะละกอ กล้วย และส้ม และคนเล่นตอบแบบนี้:
คำถามที่ 1: แอปเปิ้ล หรือ มะละกอ? ตอบมะละกอ
คำถามที่ 2: มะละกอ หรือ กล้วย? ตอบกล้วย
คำถามที่ 3: กล้วย หรือ ส้ม? ตอบกล้วย
จะได้ว่าของที่ชอบที่สุดคือกล้วย ซึ่งต้องถามทั้งหมด 3 ครั้งถึงจะได้คำตอบ
วิธีการการหาค่าสูงสุดแบบนี้เรียกว่า linear method หรือวิธีแบบไล่ทีละตัว ซึ่งถ้าเรามีตัวเลือกทั้งหมด n ตัว เราต้องใช้ n-1 คำถามเสมอเพื่อหาของที่ชอบที่สุดเสมอ เพราะมันคือการหยิบของชิ้นแรกขึ้นมาไว้ในมือ แล้วเอามาเทียบกับชิ้นถัด ๆ ไปอีก n-1 ชิ้น ถ้าเจอชิ้นที่ชอบมากกว่าก็แค่โยนของในมือทิ้งไป แล้วเอาชิ้นที่ชอบที่สุดชิ้นใหม่มาใส่แทน
แต่คำถามคือ การใช้ n-1 คำถามนี่เป็นจำนวนคำถามที่น้อยที่สุดจริงไหม หรือเราสามารถลดจำนวนครั้งของการเปรียบเทียบให้น้อยกว่านี้ได้
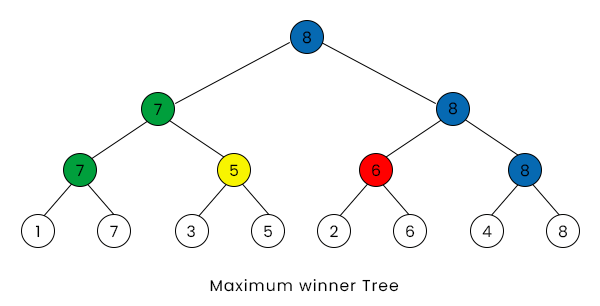
มีอีกวิธีที่ใช้เรียกว่า tournament method หรือการค้นหาแบบทัวร์นาเมนต์ คล้าย ๆ การแข่งฟุตบอลโลก วิธีนี้คือจับคู่ตัวเลือกมาเปรียบเทียบกันเป็นรอบ ๆ เช่น ถ้ามี 4 ตัวเลือก ก็จับคู่แอปเปิ้ลกับมะละกอ กล้วยกับส้ม แล้วเลือกผู้ชนะของแต่ละคู่ จากนั้นก็เอาผู้ชนะมาเจอกันในรอบชิง ก็จะได้ว่าชอบอันไหนที่สุด ซึ่งถ้าเรามีจำนวนของที่จะเอามาเทียบทั้งหมด n ซึ่งอยู่ในรูป 2 ยกกำลัง k ชิ้น เช่นพวก 2 4 8 16 32 ... เราจะได้ว่ารอบแรกต้องแข่งกันทั้งหมด n/2 จากนั้นเป็น n/4 ไล่ไปเรื่อย ๆ จนถึงคู่ชิง ซึ่งจะได้ว่าจำนวนครั้งที่ต้องแข่งทั้งหมดคือ
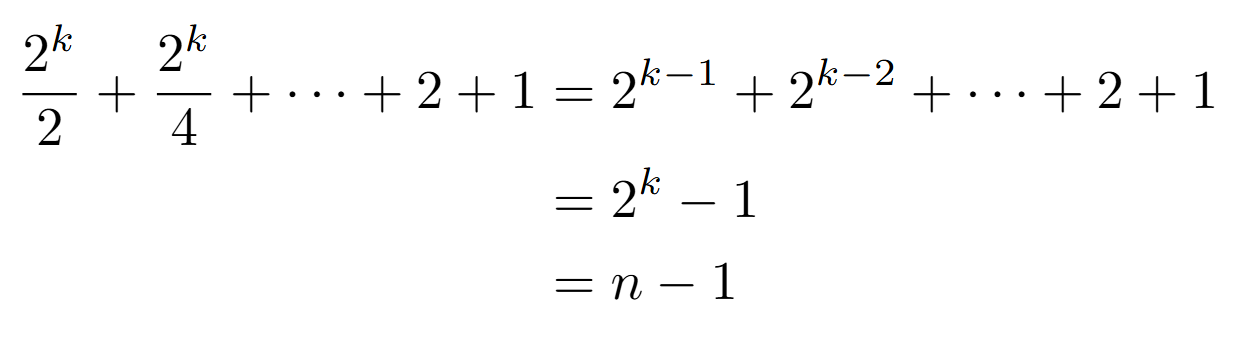
สรุปก็คือต้องใช้ n-1 คำถามซึ่งเท่ากับตอนทำ linear method เป๊ะเลย
จึงกลับมาที่คำถามของเราที่ว่า สรุปแล้วเราสามารถลดจำนวนคำถามให้น้อยกว่า n-1 ได้ไหม และคำตอบคือไม่ได้ ลองคิดตามง่าย ๆ ว่าถ้าเรามีตัวเลือก n ตัว และเราต้องการหาสิ่งที่ชอบที่สุด การถามแต่ละครั้งคือการเปรียบเทียบตัวเลือกสองตัว และผลของการเปรียบเทียบหนึ่งครั้งจะให้ข้อมูลเพียงแค่ว่าตัวไหนชนะ ซึ่งนั่นหมายความว่า เราไม่ได้ตัดตัวเลือกออกทีละหลายตัว แต่ได้ตัดออกแค่ 1 ตัวเท่านั้นในแต่ละครั้ง ดังนั้นการหาผู้ชนะต้องมีการเปรียบเทียบครบทุกตัวเลือก ถ้าเราลองถามน้อยกว่านี้ เช่น ถามแค่ n-2 คำถาม เราจะเหลือผู้เข้าแข่งขันบางตัวที่ไม่เคยถูกเปรียบเทียบเลย และนั่นหมายความว่าเราไม่มีทางมั่นใจได้เลยว่าตัวไหนคือสิ่งที่ดีที่สุดจริง ๆ เพราะยังเทียบไม่ครบทุกตัวนั่นเอง
สรุปก็คือ ทั้ง linear method และ tournament method นั้นก็ต่างเป็นวิธีการหาค่าสูงสุดที่ใช้เวลาน้อยที่สุดแล้ว ซึ่งพอถึงตรงนี้ หลายคนอาจจะคิดว่า อ้าว งั้นจะใช้วิธีไหนก็เหมือนกันสิ เพราะใช้จำนวนคำถามเท่ากันนี่นา แต่จริง ๆ แล้ว สองวิธีนี้มีข้อแตกต่างที่น่าสนใจอยู่
ถ้ามองในแง่ของหน่วยความจำที่ต้องใช้ เราพบว่าวิธี linear method ชนะขาด เพราะเราแค่ต้องจำสิ่งที่กำลังอยู่ในมือเท่านั้น ไม่ต้องจำข้อมูลอื่น ๆ แต่การทำ tournament method นั้นเราต้องจำผู้ชนะจากคู่ก่อน ๆ ด้วย จะได้รู้ว่าต่อไปต้องเอาใครมาแข่งกับใคร ซึ่งต้องใช้หน่วยความจำมากกว่า
แต่จุดเด่นหนึ่งของ tournament method คือการหาอันดับสอง คือถ้าเราไม่ได้อยากรู้แค่สิ่งที่ชอบที่สุด แต่อยากรู้ว่าชอบอันดับสองด้วย การทำ tournament method จะบอกได้ง่ายมาก เพราะอันดับสองก็คือผู้แพ้จากรอบสุดท้ายจบเลย แต่ถ้าจะหาที่สองจาก linear method นี่อาจจะต้องย้อนกลับไปค้นตั้งแต่คำถามแรก ๆ
อีกข้อที่ tournament method เหนือกว่า linear method อย่างชัดเจนคือความสามารถในการทำงานแบบขนาน หรือที่เรียกว่า parallel computing ลองนึกภาพการแข่งขันฟุตบอลโลกรอบ 8 ทีมสุดท้าย หากเราไม่กังวลเรื่องความยุ่งยากของการรับชม ความจริงแล้วสามารถจัดให้ทั้ง 4 คู่แข่งกันพร้อมกันได้เลย ซึ่งลดเวลาไปได้มาก ต่างจาก linear method ที่ต้องไล่เปรียบเทียบไปทีละคู่ตามลำดับเสมอ เพราะต้องการผลลัพธ์จากคู่ก่อนหน้ามาแข่งกันต่อ
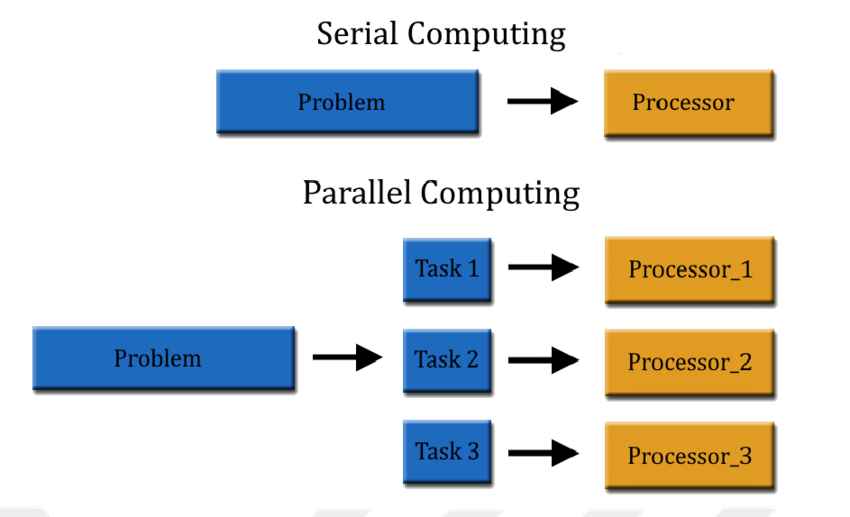
parallel computing ช่วยลดเวลาการประมวลผลไปได้อย่างมาก โดยเฉพาะเมื่อต้องการประมวลผลข้อมูลจำนวนมาก เช่น การประมวลผลบน GPU ในงาน AI หรือการใช้ระบบกระจายงานในคลาวด์ ซึ่งถูกนำไปใช้ในงานคอมพิวเตอร์ที่ซับซ้อนที่เราใช้กันอยู่ทุกวันนี้
การเลือกว่าจะใช้ linear หรือ tournament method ก็ขึ้นอยู่กับบริบทของปัญหาและทรัพยากรที่เรามี อย่างในเกม this or that ที่เลือกใช้ linear method ก็เพราะว่ามีตัวเลือกไม่กี่ชิ้น และคนดูก็จะได้ไม่ต้องคอยจำด้วยว่าใครแข่งกับใครไปแล้วบ้าง ทำให้ดูคลิปได้สนุกขึ้น และที่สำคัญคือสมองคนเราตอบคำถามหลาย ๆ ข้อพร้อมกันไม่ได้ด้วย
และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ
เอกสารอ้างอิง
https://dyclassroom.com/programming/find-the-minimum-and-maximum-number-in-an-array-using-tournament-method
https://www.geeksforgeeks.org/tournament-tree-and-binary-heap/
https://medium.com/enjoy-algorithm/find-maximum-and-minimum-in-an-array-c2049c1411e0
https://www.enjoyalgorithms.com/blog/find-the-minimum-and-maximum-value-in-an-array
https://www.heavy.ai/technical-glossary/parallel-computing