แผนที่ พิซซ่า และสัมพัทธภาพ: ความโค้งภายใต้อิทธิพลของเกาส์

แผนที่ - น. แบบที่เขียนย่อจากพื้นดิน บอกแม่นํ้า ฝั่งทะเล และอื่น ๆ

ข้างต้นนี้คือคำจำกัดความของแผนที่ในพจนานุกรม ฉบับราชบัณฑิตยสภา พ.ศ. ๒๕๕๔ ราวกับว่าแผนที่นั้นคือสิ่งที่แสดงความจริงอันเป็นภววิสัย (objectivity) กล่าวคือไม่ขึ้นอยู่กับมุมมองของผู้เขียน/อ่านมัน (subjectivity)

แต่มันเป็นเช่นนั้นจริง ๆ หรือ? หรือความจริงแล้วแผนที่ที่เรารู้จักกำลังลวงเราให้เชื่อเช่นนั้น แผนที่สร้างความจริงชุดหนึ่งให้เรารับรู้ แทนที่จะแสดงความเป็นจริง

ประเด็นข้างต้นนั้นในแง่หนึ่งเป็นประเด็นทางสังคม ที่ถ้าใครสนใจอาจจะลองไปหาหาหนังสือ กำเนิดสยามจากแผนที่ ของ ธงชัย วินิจจะกูล มาอ่าน สำหรับบทความนี้เราจะโฟกัสไปที่คณิตศาสตร์เกี่ยวกับแผนที่ที่ชี้ให้เห็นความไม่สมบูรณ์แบบของแผนที่ในแง่มุมหนึ่ง

มาเริ่มกันด้วยคำถามง่าย ๆ

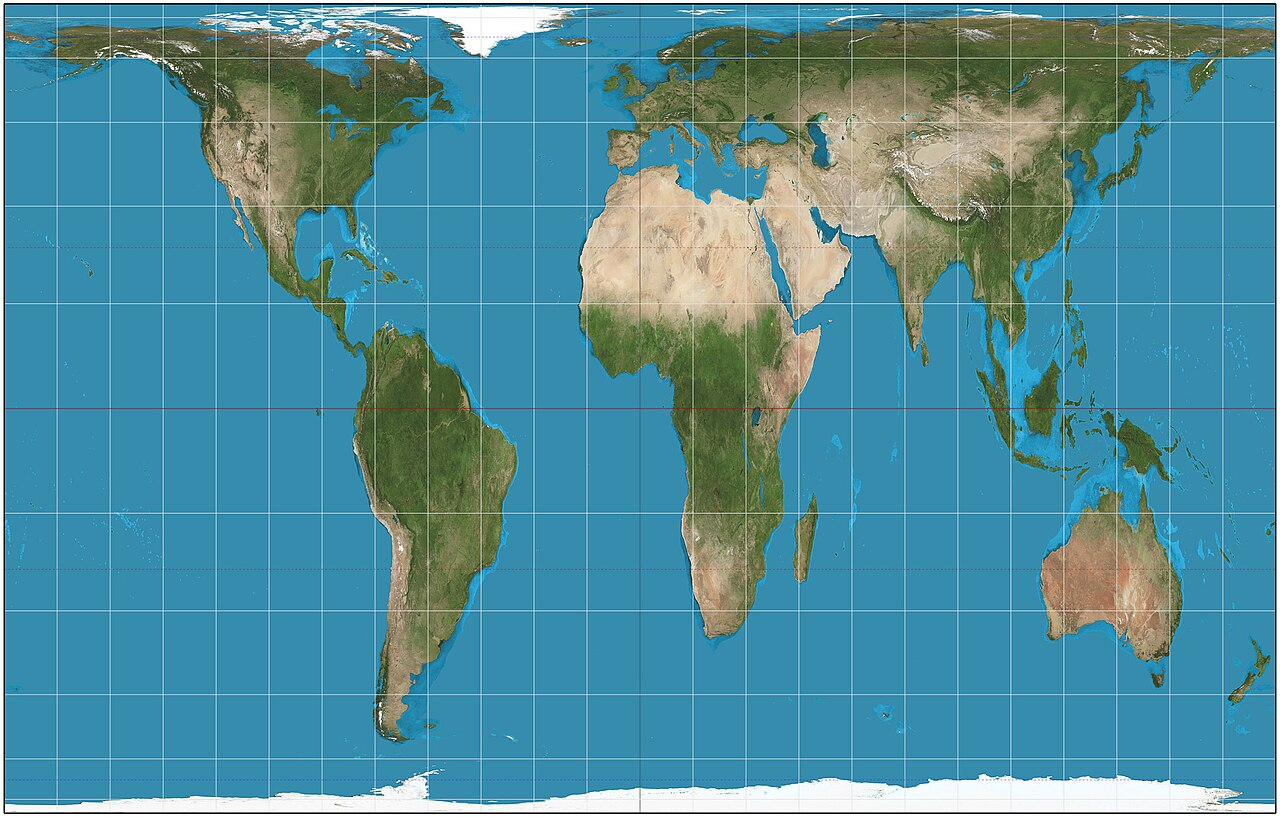
ลองนึกภาพแผนที่โลกในหัว (ถ้านึกไม่ออกก็ดูภาพข้างล่างนี้) แล้วลองตอบว่า ระหว่างกรีนแลนด์กับออสเตรเลีย ประเทศไหนใหญ่กว่ากัน?

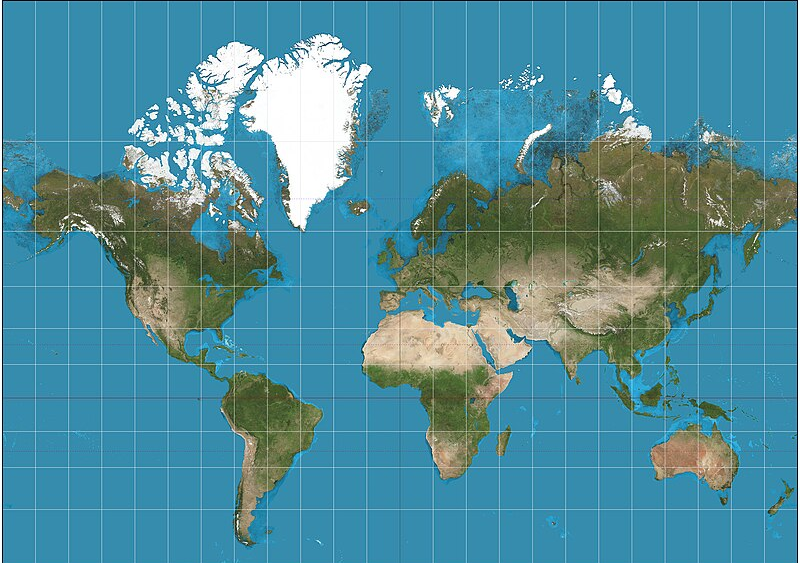
คำตอบที่ถูกต้องคือ ออสเตรเลีย ซึ่งมีขนาด 7,692,024 ตารางกิโลเมตร ในขณะที่กรีนแลนด์มีขนาดเพียง 2,166,086 ตารางกิโลเมตร หรือก็คือเล็กกว่าหนึ่งในสามของออสเตรเลียเสียอีก (ข้อมูลพื้นที่จาก worldometers)

ทำไมถึงเป็นอย่างนั้นกันนะ?

นั่นก็เพราะแผนที่มันหลอกตาเรายังไงล่ะ! วิดิโอข้างล่างนี้แสดงให้เห็นขนาดที่แท้จริงของแต่ละประเทศ หรือจะลองเข้าไปเลื่อนแผนที่ประเทศไปทับประเทศอื่นเพื่อเทียบขนาดจริงได้ที่เว็บไซต์นี้ thetruesize.com

ถึงตอนนี้บางคนอาจจะสังเกตเห็นแล้วว่า ขนาดในแผนที่ของประเทศแถบศูนย์สูตรอย่างไทยเรานั้น ไม่ได้เปลี่ยนแปลงไปมากเทียบกับประเทศที่อยู่ไกลจากศูนย์สูตร ซึ่งเป็นเพราะเหตุใดจะมาอธิบายให้ฟัง

ก่อนอื่น ขอเริ่มจากคำถามที่ว่า "แผนที่คืออะไร" จากมุมมองทางคณิตศาสตร์

คำตอบคือ แผนที่ คือ ฟังก์ชัน (function) ประเภทหนึ่ง โดยทั่วไป เรามักจะนึกถึงฟังก์ชันในรูปแบบของ f(x) ที่ส่งจำนวนค่าหนึ่งไปยังอีกค่าหนึ่ง เช่น f(x)=x+1 จะส่ง 0 ไป 1 และส่ง 1 ไป 2 ฯลฯ แต่โดยทั่วไป input และ output ของฟังก์ชันไม่ได้จำเป็นต้องเป็นตัวเลขโดด ๆ เสมอไป ในกรณีของแผนที่ มันคือฟังก์ชัน (แบบหนึ่งต่อหนึ่งและทั่วถึง) ที่ส่งจากทรงกลม (สมมติว่าโลกมันกลมดิ๊ก) ไปยังแผ่นกระดาษหรือระนาบนั่นเอง

อันที่จริงบ่อยครั้งนักคณิตศาสตร์ก็เรียกฟังก์ชันว่า "map" เสียด้วยซ้ำ

แต่การจะสร้างฟังก์ชันจากทรงกลมไปยังแผ่นกระดาษนั้นก็สร้างได้หลายแบบด้วยกัน คำถามคือเราควรจะใช้ฟังก์ชันแบบไหนในการวาดแผนที่โลก

แน่นอนว่าแผนที่ (ในอุดมคติ) มันควรจะเป็นภาพแทนของโลกที่ไม่บิดเบี้ยว กล่าวคือมันควรจะรักษาสัดส่วนของระยะทางระหว่างจุดต่าง ๆ บนแผนที่ ตัวอย่างง่าย ๆ ของฟังก์ชันที่รักษาสัดส่วนก็คือการซูมรูปภาพ ซึ่งเป็นฟังก์ชันจากระนาบไปยังระนาบ ในทางคณิตศาสตร์เราสามารถอธิบายฟังก์ชันการซูมได้ด้วยสมการ f(x,y)=(kx,ky) เมื่อ (x,y) แทนจุดบนระนาบ และ k คืออัตราการขยาย

เมื่อ k=1 ฟังก์ชันนี้จะรักษาระยะทางระหว่างจุด หรือที่มีชื่อเฉพาะว่า isometry ฟังก์ชันประเภทนี้บนระนาบก็เช่น การเลื่อนขนานและการหมุน ถ้าเรามีฟังก์ชัน isometry จากผิวโลกไปยังระนาบ เราย่อมสามารถซูมเข้าซูมออกเพื่อเปลี่ยนสัดส่วนของแผนที่ได้ไม่ยาก ดังนั้นในที่นี้เราจะพิจารณาเฉพาะฟังก์ชัน isometry จากผิวโลกไปยังระนาบ

อย่างที่บอกไป นี่คือสมบัติในอุดมคติที่เราอยากให้แผนที่มี แต่ปัญหาคือในทางคณิตศาสตร์แล้ว ฟังก์ชันลักษณะนี้ไม่มีอยู่จริง! กล่าวคือไม่ว่าเราจะวาดแผนที่โลกด้วยเทคนิคไหน มันก็จะเกิดการบิดเบี้ยว

ก่อนที่จะลงรายละเอียดไปที่ประเด็นนี้ เราย้อนมาดูแผนที่แบบที่เราคุ้นเคยกันอีกครั้ง

แผนที่โลกที่เห็นข้างบนนี้ นั้นเป็นแผนที่วาดด้วยฟังก์ชันการฉายแบบ Mercator หรือ Mercator projection ฟังก์ชันนี้สามารถอธิบายได้ง่าย ๆ ด้วยรูปข้างล่าง กล่าวคือให้เราเอาแผนกระดาษมาม้วนเป็นทรงกระบอกรอบทรงกลม ทีนี้ฉายแสงจากจุดศูนย์กลางของทรงกลม จุดที่อยู่บนทรงกลมนั้นจะถูกส่งไปยังจุดที่อยู่บนกระดาษตามแนวรังสีที่ฉาย

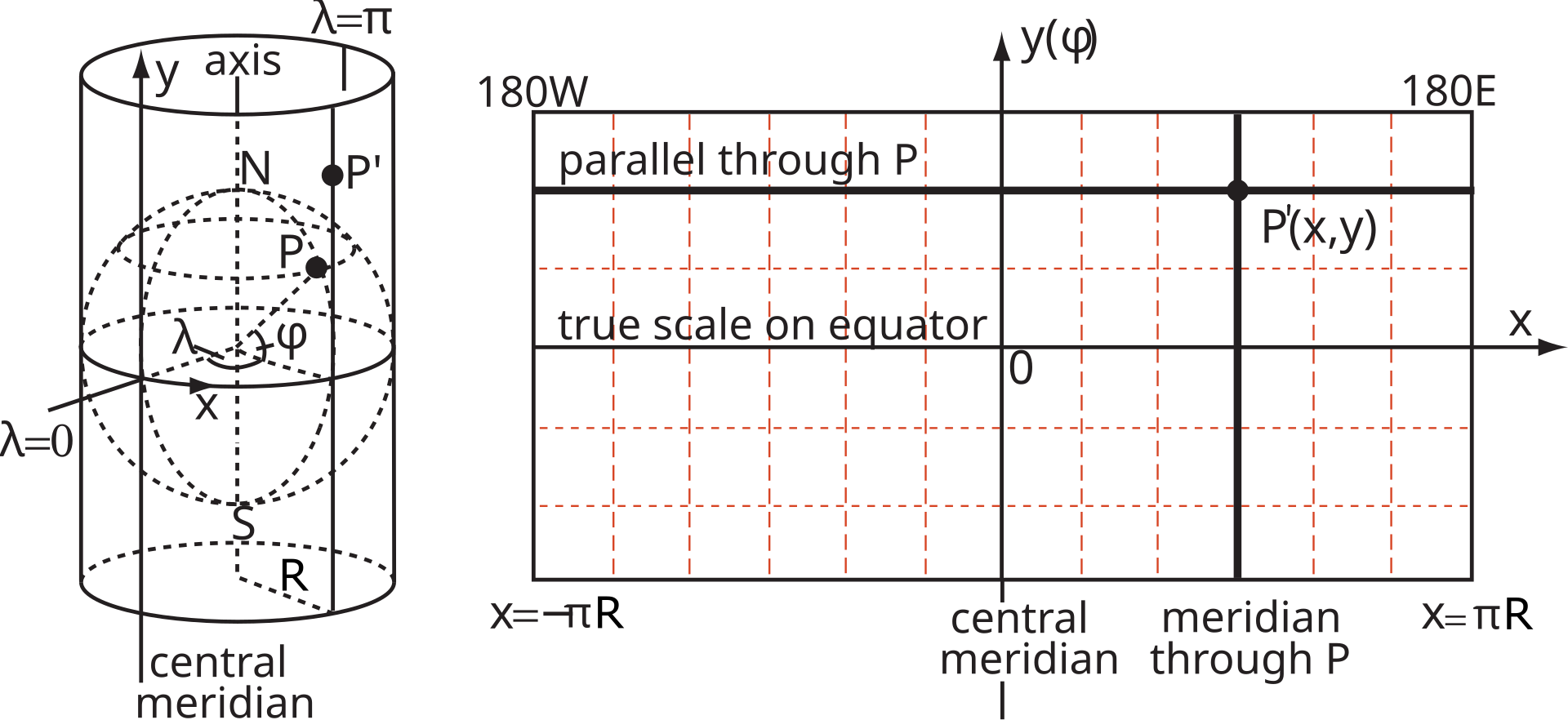
เวลาที่เราฉายแสงไปตกกระทบฉาก เมื่อฉากอยู่ไกล วงแสงก็จะยิ่งใหญ่ขึ้น ในกรณีนี้ก็ไม่ต่างกัน บริเวณเส้นศูนย์สูตร ระยะทางบนกระดาษจะเท่ากับระยะทางบนทรงกลม แต่สำหรับจุดที่อยู่ใกล้ขั้วโลก ระยะทางบนกระดาษจะถูกขยายออก นี่เองคือสาเหตุที่ทำให้พื้นที่ของประเทศใกล้ขั้วโลกดูใหญ่กว่าความเป็นจริง

ถึงแม้ว่ามันจะไม่รักษาระยะทาง แต่ Mercator projection กลับเป็นฟังก์ชันที่รักษามุม และทำให้มันมีประโยชน์ในการเดินเรือ และกลายเป็นรูปแบบของแผนที่ที่ถูกใช้กันอย่างแพร่หลายไปในที่สุด

แผนที่อีกแบบที่มีสมบัติรักษามุมคือแผนที่แบบ Stereographic projection ซึ่งเป็นการเอาทรงกลมมาวางบนระนาบแล้วฉายแสงจากขั้วโลกเหนือ ส่องผ่านจุดไปลงบนระนาบข้างล่าง ซึ่งแผนที่ที่ได้ออกมาจะมีรูปร่างแปลกตาไปเสียหน่อย

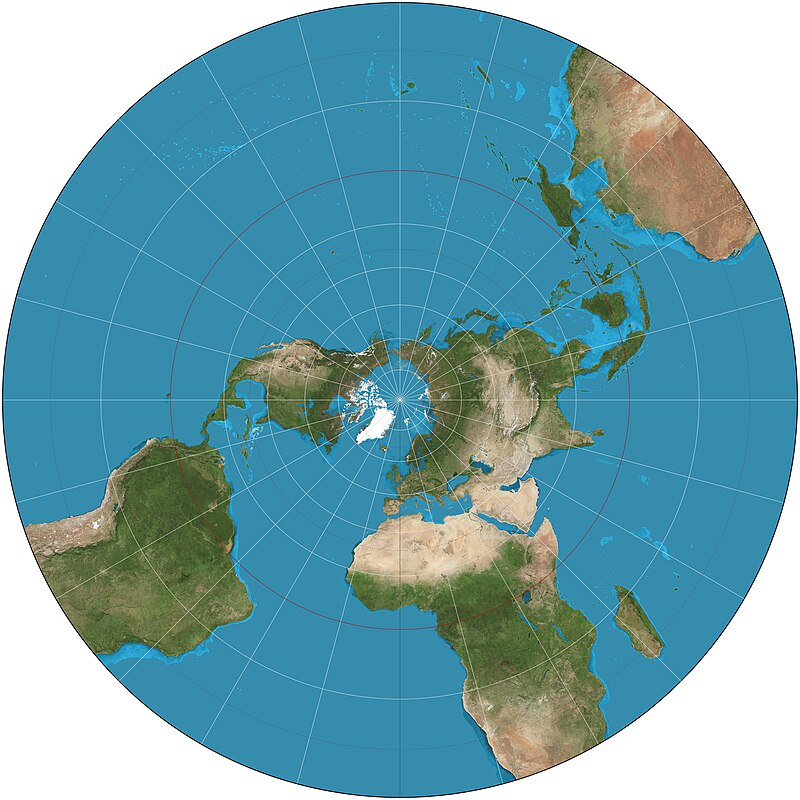
นอกจากนี้แล้วก็ยังมีแผนที่ที่รักษาพื้นที่ เรียกว่า Gall–Peters projection หากแต่แผนที่ประเภทนี้จะไม่รักษามุม ข้างล่างคือหน้าตาของแผนที่ประเทศนี้ จะเห็นว่าบริเวณขอบบนล่างของแผนที่หดเล็กไปมากเมื่อเทียบกับแผนที่แบบ Mercator

อย่างที่บอกไป แผนที่แบบสมบูรณ์แบบนั้นไม่มีอยู่จริง เราจึงต้องเลือกว่าจะใช้แผนที่แบบไหน แต่ก็ควรพึงระลึกไว้เสมอว่ามันมีบางอย่างผิดเพี้ยนไปเสมอ

ถึงตรงนี้คงได้เวลาย้อนกลับไปอธิบายว่าเหตุใดแผนที่ในอุดมคติแบบนั้นถึงไม่มีอยู่จริง

คณิตศาสตร์ที่อยู่เบื้องหลังเรื่องราวนี้คือ เรขาคณิตเชิงอนุพันธ์ หรือ Differential geometry ซึ่งได้รับการพัฒนาขึ้นโดย คาร์ล ฟรีดริช เกาส์ (1777–1855) นักคณิตศาสตร์ชื่อดังชาวเยอรมัน อันที่จริงการไม่มีอยู่ของแผนที่ที่สมบูรณ์แบบนั้นก็เป็นผลพวงของทฤษฎีบทสำคัญที่เกาส์เป็นผู้พิสูจน์ Theorema Egregium (ภาษาละตินของ Remarkable Theorem) ที่แปลว่า ทฤษฎีบทอันน่าทึ่ง (แน่นอนว่าเกาส์เป็นคนตั้งชื่อทฤษฎีบทนี้ด้วยตัวเขาเอง)

อันที่จริงแล้วความสนใจของเกาส์ต่อวิชาเรขาคณิตก็ไม่ได้มาจากไหนไกลเลย มันมาจากประสบการณ์ทำงานที่เขาเคยได้ไปช่วยร่างแผนที่นี่แหละ! (อย่าลืมว่าภาษาอังกฤษของเรขาคณิตคือ "Geo"metry หรือก็คือ วิชาวัดโลก นั่นเอง) เรื่องราวส่วนนี้ของชีวิตเกาส์ถูกเล่าเอาไว้ในนวนิยายเยอรมันเรื่อง คนวัดโลก (Die Vermessung der Welt) ตามท้องเรื่องของนวนิยายเรื่องนี้ ดูเหมือนเกาส์จะไม่ค่อยถูกโฉลกกับงานภาคสนามเท่าใดนัก ตัวละครเกาส์ถูกนำเสนอในลักษณะที่เป็นคู่ตรงข้ามของนักธรณีวิทยา อเล็กซานเดอร์ ฟอน ฮุมโบลท์

"ข้าพเจ้าไม่เข้าใจว่า เหตุใดจึงต้องไปค้นหาความจริงจากข้างนอก ในเมื่อความจริงย่อมเป็นความจริงในทุก ๆ ที่" เกาส์ (ในนวนิยาย) รำพึง

บางทีนั่นอาจจะเป็นสาเหตุที่เขาหวนกลับมาตรึกตรองปัญหาเชิงนามธรรมของการร่างแผนที่อยู่ที่บ้านแทนที่จะออกไปร่างแผนที่อย่างเป็นรูปธรรม

ทฤษฎีบทอันน่าทึ่งของเกาส์นั้นเกี่ยวข้องกับความโค้ง (curvature) ของพื้นผิว ซึ่งเป็นค่าตัวเลข ณ จุดหนึ่ง ๆ บนพื้นผิว ทุกวันนี้ค่าความโค้งนี้เป็นที่รู้จักกันในนาม Gaussian curvature

ก่อนที่จะไปพูดถึงความโค้งของพื้นผิว ลองมาดูวัตถุที่มีมิติน้อยกว่านั้นก็คือเส้น 1 มิติ ตัวอย่างง่าย ๆ ก็เช่นเส้นตรง ซึ่งไม่มีความโค้ง และวงกลม ซึ่งโค้งเท่า ๆ กันทุกจุด

วงกลมที่มีขนาดใหญ่จะมีความโค้งน้อยกว่า นี่เป็นการเปรียบเทียบในเชิงคุณภาพ แต่ในทางคณิตศาสตร์เราสามารถคำนวณความโค้งออกมาเป็นตัวเลขได้ ในกรณีของทรงกลม แต่ละจุดจะมีความโค้ง 1/r เมื่อ r คือรัศมีของวงกลม สำหรับเส้นโค้งอื่น ๆ แต่จะจุดก็จะมีค่าความโค้งแตกต่างกันไป

ปัญหาในการวัดค่าความโค้งของพื้นผิวสองมิติก็คือมันจะมีทิศทางเข้ามาเกี่ยวข้อง กล่าวคือ ณ จุด ๆ หนึ่ง ถ้าเราลากเส้นผ่านจุดนั้นในทิศทางต่าง ๆ เราก็จะสามารถวัดความโค้งของเส้นนั้น ๆ ได้ ตัวอย่างก็เช่น ผิวทรงกระบอกรัศมี r ถ้ามองเส้นตัดขวางก็จะเป็นวงกลมที่มีความโค้ง 1/r แต่ถ้ามองเส้นตามความยาว มันก็จะเป็นเส้นตรงที่มีความโค้งเป็น 0

ในกรณีของทรงกลมรัศมี r เนื่องจากความสมมาตรของมัน ไม่ว่าเราจะตัดมันจากทิศทางไหน ก็จะได้วงกลม รัศมี r ที่มีความโค้งเป็น 1/r เสมอ

พื้นผิวที่น่าสนใจอีกรูปแบบหนึ่งคือผิวอานม้า (ภาพข้างล่าง และที่กล่าวถึงไปในบทความ ปลาจะรู้รูปร่างของบ่อที่มันอยู่ได้ยังไง โดยผมเอง) ซึ่งเมื่อมองจากคนละทิศทางจะมีความโค้งไปคนละด้านกัน กล่าวคือทิศทางหนึ่งมีความโค้งเป็นบวก ส่วนอีกทิศทางมีความโค้งเป็นลบ

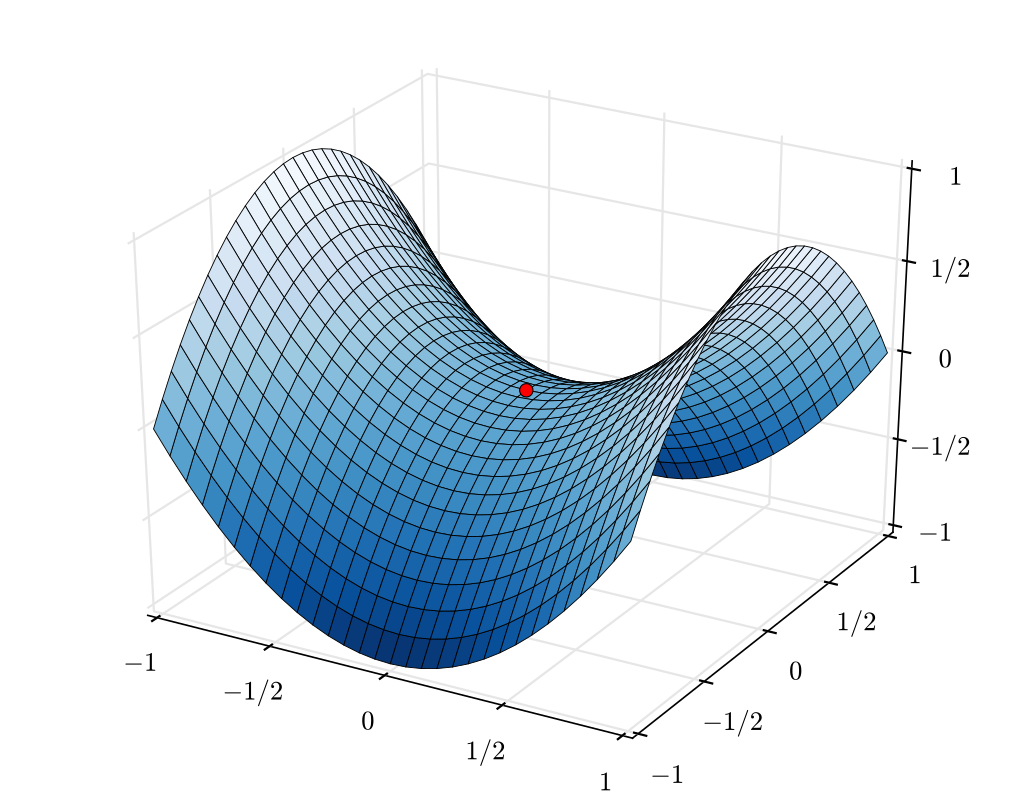
คำถามคือ ณ จุด ๆ หนึ่งบนพื้นผิว เราสามารถอธิบายความโค้ง ณ จุดนั้นออกมาเป็นค่าตัวเลขค่าหนึ่ง (โดยไม่สนใจเรื่องทิศทาง) ได้หรือไม่? สิ่งที่เกาส์เสนอคือ ในบรรดาความโค้งตามทิศทางเหล่านี้ จะมีความโค้งค่ามากสุดและค่าน้อยสุด ให้นำความโค้งสองค่านี้มาคูณกัน ต่านี้เองที่เรียกกันว่า Gaussian curvature

ตัวอย่างเช่น ทรงกระบอกรัศมี r ที่แต่ละจุดจะมีความโค้งมากสุดคือ 1/r และน้อยที่สุดคือ 0 ดังนั้นจึงมี Gaussian curvature เป็น 0 ทุกจุด กล่าวอีกนียหนึ่งคือในมุมมองนี้ ทรงกระบอกเป็นพื้นผิวที่ไม่มีความโค้ง

สำหรับทรงกลมรัศมี r จะมี Gaussian curvature เป็น 1/r^2 สังเกตว่าค่านี้เป็นบวกและเท่ากันทุกจุดบนทรงกลม สำหรับผิวอานม้า ด้วยความที่มีทิศทางที่ความโค้งเป็นบวกและลบ Gaussian curvature ซึ่งเป็นผลคูณของค่ามากสุดและน้อยสุด จึงมีค่าเป็นลบ

ทฤษฎีบทอันน่าทึ่งของเกาส์บอกกับเราว่า ค่า Gaussian curvature จะไม่เปลี่ยนแปลงภายใต้ isometry เกล่าคือถ้าเรามีฟังก์ชันที่รักษาระยะทางจากพื้นผิวหนึ่งไปอีกพื้นผิวหนึ่ง ถ้าจุด x ถูกส่งไปยังจุด y ภายใต้ฟังก์ชันนี้ ค่า Gaussian curvature ของจุด x จะต้องเท่ากับของจุด y

ดังนั้นมันจึงเป็นไปไม่ได้ที่จะมี isometry จากทรงกลม (ความโค้งเป็นบวกทุกจุด) ไปยังแผ่นกระดาษ (ความโค้งเป็น 0 ทุกจุด) กล่าวคือเป็นไปไม่ได้ที่จะมีแผนที่ที่สมบูรณ์แบบนั่นเอง

ในบทตัดจากหนังสือ Mapmatics: A Mathematician's Guide to Navigating the World ตอนหนึ่ง ผู้เขียน Paulina Rowińska กล่าวถึงผลประโยชน์ทางอ้อมของทฤษฎีบทของเกาส์ต่อการกินพิซซ่า!? (แม้ว่าเกาส์คงจะไม่เคยได้ใช้มัน เพราะว่าเขาไม่เคยมีโอกาสกินอาหารอิตาเลียนจานนี้)

พิซซ่าเมื่ออยู่ในถาดนั้นจะมีลักษณะเป็นแผ่นราบ ไม่มีความโค้งใด ๆ ดังนั้น Gaussian curvature จึงเป็น 0 (รูป a) แน่นอนว่าเมื่อเรายกพิซซ่าขึ้น มันย่อมเกิดการบิดเบี้ยว แต่มันเป็นการบิดเบี้ยวแบบ isometry ดังนั้นแม้ว่ามันจะโค้งงอไป แต่ค่า Gaussian curvature ของมันจะต้องยังเท่ากับ 0 นั่นเท่ากับว่า ณ จุดหนึ่ง ๆ บนพิซซ่าจะต้องมีทิศทางหนึ่งที่มีความโค้งเป็น 0

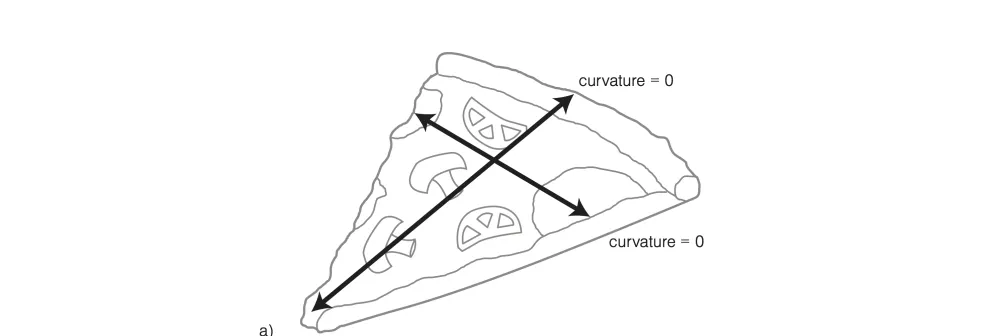
รูปแบบหนึ่งที่เกิดขึ้นได้ก็คือรูป b ข้างล่างนี้ ซึ่งเป็นรูปร่างที่ทำให้การกินพิซซ่าของเรามันลำบากลำบน ปลายหางของมันรังแต่จะย้วยลงไม่เข้าปากเรา ที่เป็นแบบนี้ก็เพราะแม้ Gaussian curvature จะเป็น 0 เสมอ แต่ความโค้งในแนวยาวของพิซซ่าเปลี่ยนแปลงได้ ในขณะที่ความโค้งในแนวขวางยังคงเป็น 0 เท่าเดิม

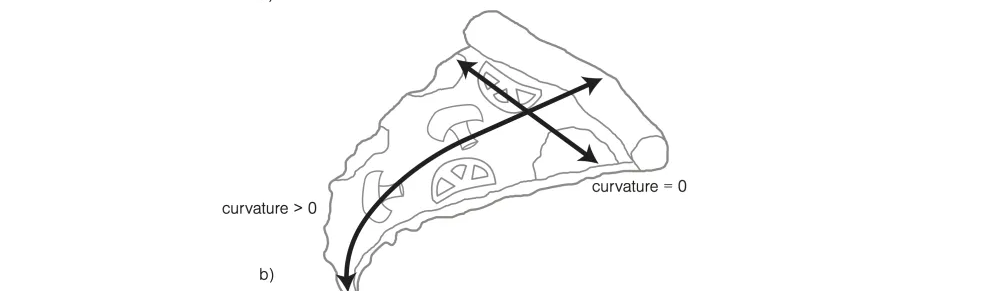
ในทางกลับกัน ถ้าเราถือพิซซ่าตามรูป c ความโค้งในแนวยาวจะเป็น 0 แน่นอนว่าเรายังบีบให้พิซซ่าโค้งมากขึ้นตามแนวขวางได้ แต่ตามแนวยาวความโค้งจะเป็น 0 ไม่เปลี่ยนแปลง เพราะ Gaussian curvature ที่เป็นผลคูณจะต้องคงที่เป็น 0 เสมอ! และนี้คือบทพิสูจน์ทางคณิตศาสตร์ว่าทำไมการถือพิซซ่าแบบนี้จะทำให้มันไม่ย้วย

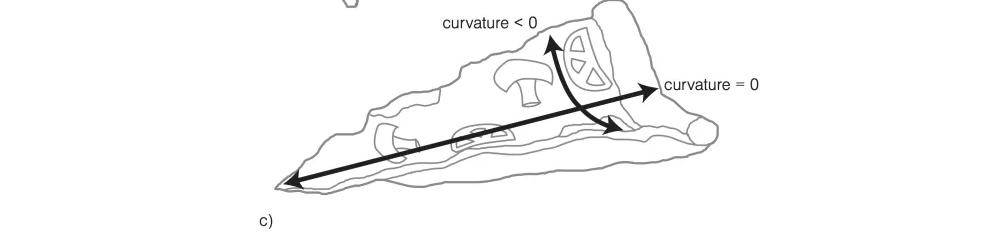
ไม่น่าเชื่อว่าทฤษฎีบททางเรขาคณิตจะสามารถนำเอามาอธิบายว่าเหตุใดการกินพิซซ่าตามรูป c ถึงเป็นการกินที่สะดวกที่สุด

ภายหลังผลงานชิ้นเอกชิ้นนี้ของเกาส์ เขาก็ได้ยุยงให้นักคณิตศาสตร์รุ่นต่อมาอย่าง แบร์นฮาร์ท รีมัน (1826-1866) ต่อยอดแนวคิด (ตอนนำเสนอผลงานต่อหน้าสาธารณชนเพื่อพิจารณารับตำแหน่งอาจารย์ ทั้ง ๆ ที่รีมันตั้งใจจะนำเสนอหัวข้ออื่น) อันกลายเป็นรากฐานของ Riemannian geometry ซึ่งศึกษาความโค้งของรูปทรงทางเรขาคณิตในมิติที่สูง ๆ ขึ้นไป และทฤษฎีนี้ท้ายที่สุดก็บันดาลให้ไอน์สไตน์หยิบยกเอาไปใช้อธิบายความโน้มถ่วงในทฤษฎีสัมพัทธภาพทั่วไปอันโด่งดัง ซึ่งตามทฤษฎีนี้ความโน้มถ่วงนั้นหาใช่สิ่งใดหากแต่คือ ความโค้งของกาล-อวกาศ นั่นเอง

อ้างอิงและหนังสือชวนอ่าน

• https://www.hup.harvard.edu/features/stopping-for-directions-how-karl-friedrich-gauss-and-pizza-help-get-us-where-we-need-to-go
• https://sites.lsa.umich.edu/qmss/2022/06/14/why-your-view-of-the-world-may-be-completely-wrong/
• Mapmatics: A Mathematician's Guide to Navigating the World เขียน-Paulina Rowińska, สำนักพิมพ์ Harvard University Press
• คนวัดโลก เขียน-ดานีเอล เคห์ลมันน์, แปล-เจนจิรา เสรีโยธิน, สำนักพิมพ์ไลบรารี่ เฮ้าส์
• กำเนิดสยามจากแผนที่ เขียน-ธงชัย วินิจจะกูล, แปล-พวงทอง ภวัครพันธุ์, ไอดา อรุณวงศ์, พงษ์เลิศ พงษ์วนานต์, สำนักพิมพ์อ่าน