ปลาจะรู้รูปร่างของบ่อที่มันอยู่ได้ยังไง
สมมติว่าคุณเป็นปลาตัวหนึ่ง ด้วยเหตุบางประการ คุณถูกขังอยู่ในภาชนะปิดที่มีน้ำนอนก้นอยู่และมีรูเล็ก ๆ ข้างบนพอให้น้ำหยดลงมาปริมาณหนึ่งทุก ๆ วัน ด้วยความที่ไม่มีแสงส่องถึง คุณจึงไม่สามารถรู้ได้ว่าภาชนะที่คุณอาศัยอยู่นั้นมีรูปทรงอะไร แต่กระนั้นด้วยความสงสัยใคร่รู้ บวกกับความว่างของคุณ คุณจึงอยากจะรู้ให้ได้ว่าคุณอาศัยอยู่ในภาชนะรูปทรงอะไร
คำถามคือคุณจะไขปริศนาข้อนี้อย่างไร?
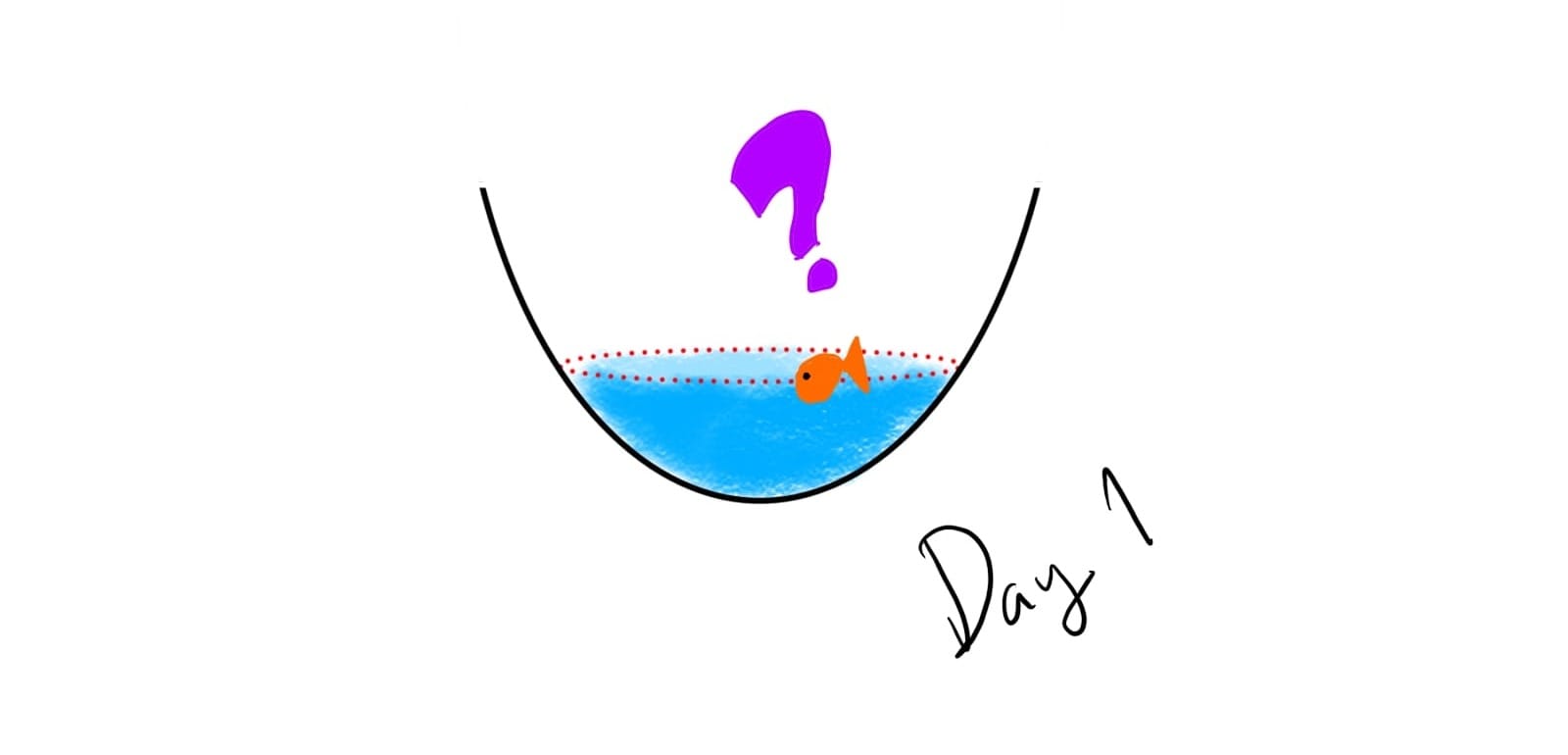
คุณหยุดคิดอยู่ครู่หนึ่งจึงตระหนักว่าถึงแม้คุณจะไม่สามารถรู้รูปทรงของภาชนะ แต่คุณยังสามารถรู้รูปร่างของผิวน้ำได้ คิดได้เช่นนั้นคุณจึงลองว่ายสำรวจไปตามผิวน้ำอันตื้นเขิน คุณบอกได้ว่าหน้าน้ำในวันนั้นเป็นรูปวงกลมหนึ่งวง
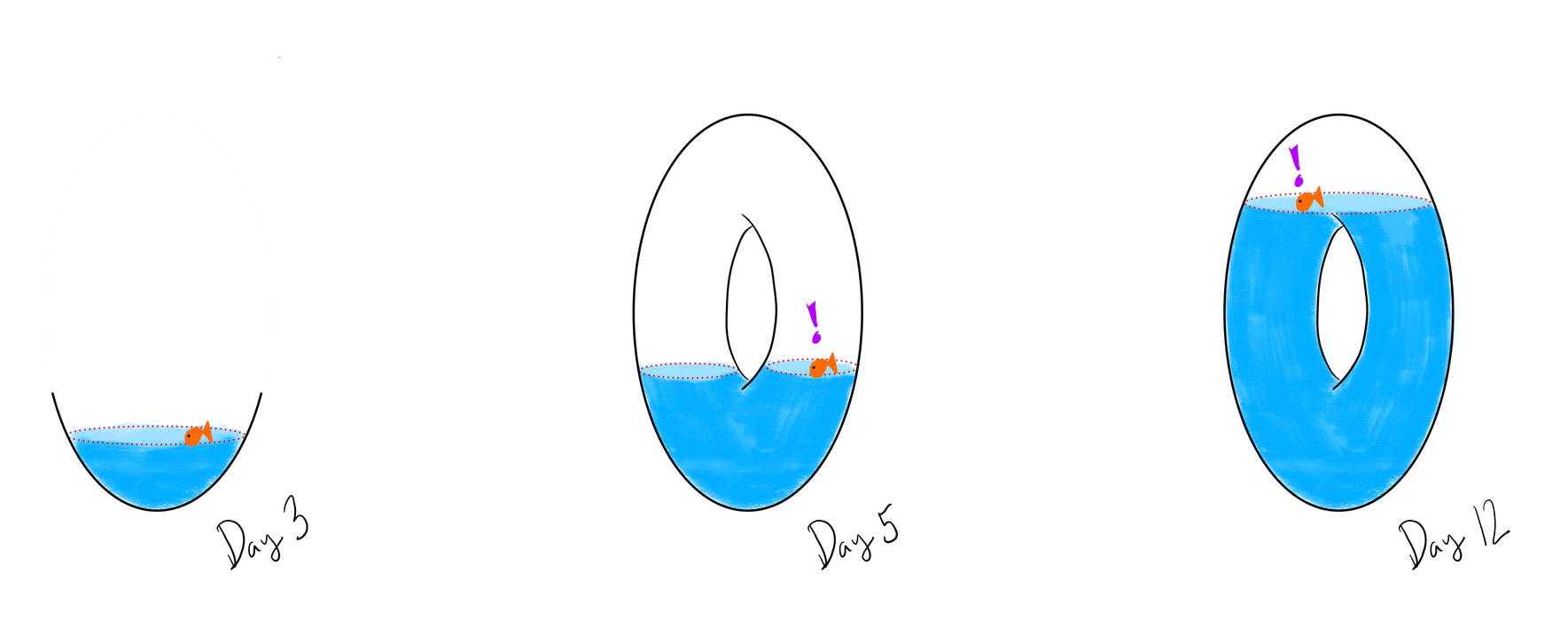
เหตุด้วยในภาชนะปิดแห่งนี้ไม่มีอะไรให้คุณทำมากนัก คุณจึงเริ่มว่ายสำรวจผิวน้ำเป็นกิจวัตรทุกวี่วัน สี่วันแรก ผิวน้ำที่สูงขึ้นนั้นยังคงมีรูปทรงเดิมเพียงแค่กว้างขึ้น แต่แล้วในวันที่ห้า คุณกลับพบว่าผิวน้ำแตกออกเป็นสองผิวที่แยกออกจากกัน คุณยังคงสำรวจผิวน้ำเช่นนั้นต่อไป จนในวันที่สิบสอง คุณจึงพบว่าผิวน้ำกลับมารวมกันเป็นวงกลมหนึ่งวงอีกครั้ง คราวนี้วงกลมค่อย ๆ เล็กลงในแต่ละวัน และในวันที่สิบแปดน้ำก็ขึ้นไปมิดภาชนะ
ตอนนั้นเองที่คุณได้คำตอบของปริศนา: ภาชนะนี้มีรูปทรงเหมือนโดนัท!
เหตุการณ์สมมติข้างต้น อาจฟังดูเหมือนปริศนาง่าย ๆ หากแต่มันคือแนวคิดสำคัญของการศึกษาปัญหาทางเรขาคณิตที่ซับซ้อนกว่านั้นมาก
น่าเศร้าที่ถึงคุณจะไขปริศนาข้อนี้ออก แต่คุณก็ยังไม่พบทางออกไปจากบ่อโดนัทอยู่ดี ดังนั้นคุณจึงใช้เวลาครุ่นคิดพิจารณาถึงคณิตศาสตร์ที่แฝงอยู่เบื้องหลังการไขปริศนาข้อนี้จนกระทั่งคุณบรรลุวิชา Morse Theory ศาสตร์แห่งการศึกษารูปทรงผ่านการดูการเปลี่ยนแปลงของหน้าตัดที่ระดับต่าง ๆ ด้วยตัวเอง !
ลองย้อนกลับมาดูผลการสำรวจผิวน้ำในภาชนะกันอีกครั้ง ในตอนนี้เรารู้แล้วว่ารูปทรงของภาชนะเป็นรูปโดนัทที่ตั้งขึ้น ทีนี้ลองสำรวจหน้าตัดของมันตั้งแต่ จุดต่ำสุด ไปจนถึง จุดสูงสุด กันอีกครั้ง เราจะเห็นว่ารูปร่างของหน้าตัดมีการเปลี่ยนแปลงคร่าว ๆ ดังนี้
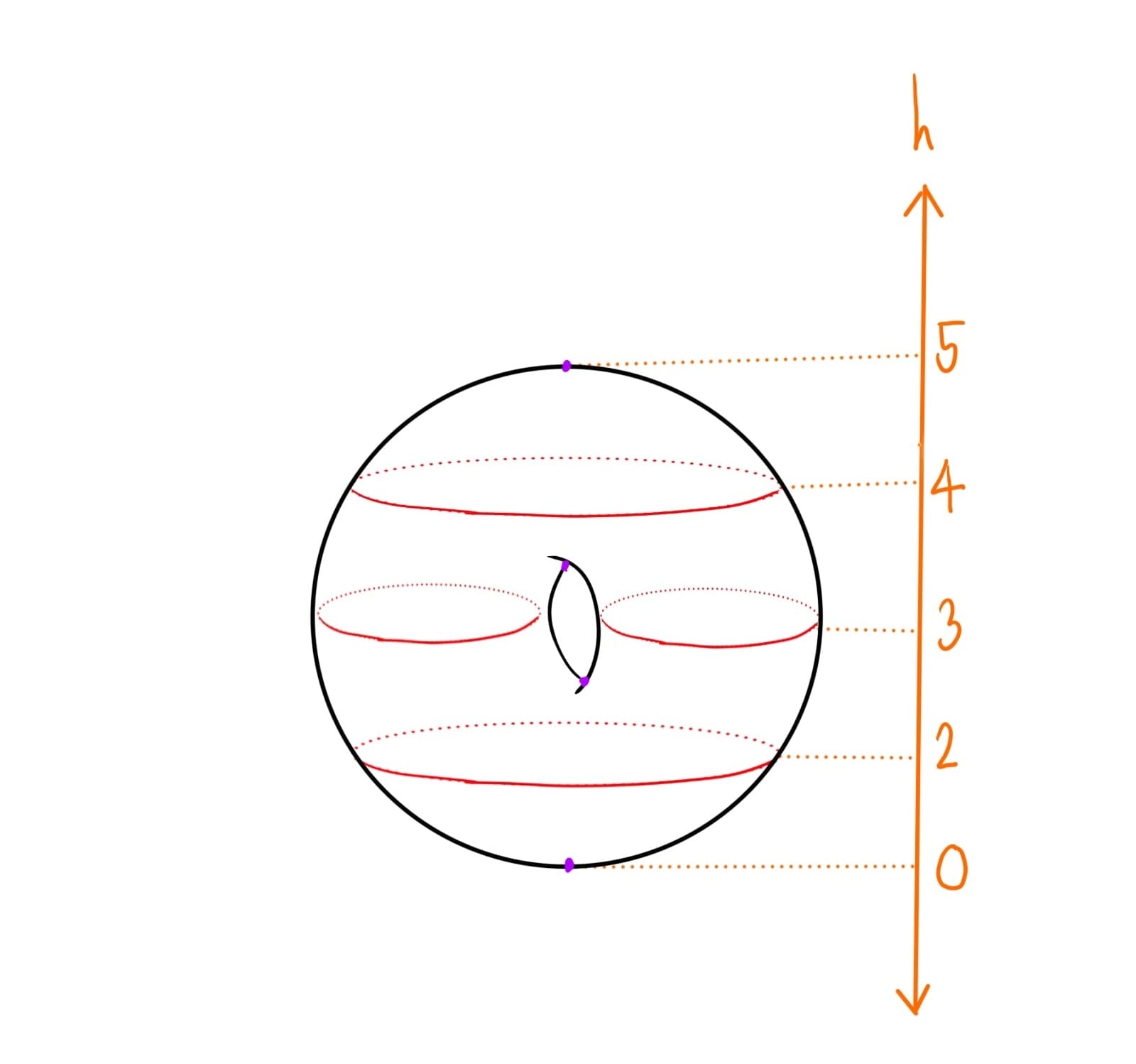
จุด → วงกลม 1 วง → วงกลม 2 วง → วงกลม 1 วง → จุด
มีการเปลี่ยนแปลงของรูปร่างหลัก ๆ อยู่ทั้งหมด 4 ครั้งด้วยกัน ขอให้เก็บข้อสังเกตง่าย ๆ นี้ไว้ในใจสักครู่ก่อน ทีนี้แทนที่จะเก็บข้อมูลแค่หน้าตัด ณ ความสูงหนึ่ง ๆ ให้ลองเก็บข้อมูลรูปทรงจากจุดต่ำสุดขึ้นมาถึงความสูงที่กำหนด เราจะเห็นการเปลี่ยนแปลงดังนี้
จุด → จาน → ท่อโค้ง → แกลลอนแบบเปิดฝา → โดนัท
คราวนี้ลองเปลี่ยนรูปทรงของภาชนะเป็นรูปทรงที่ง่ายขึ้นอย่างทรงกลม เมื่อเราไล่ดูจากจุดต่ำสุดไปจนถึงจุดสูงสุด จะเห็นรูปแบบการเปลี่ยนแปลงดังนี้
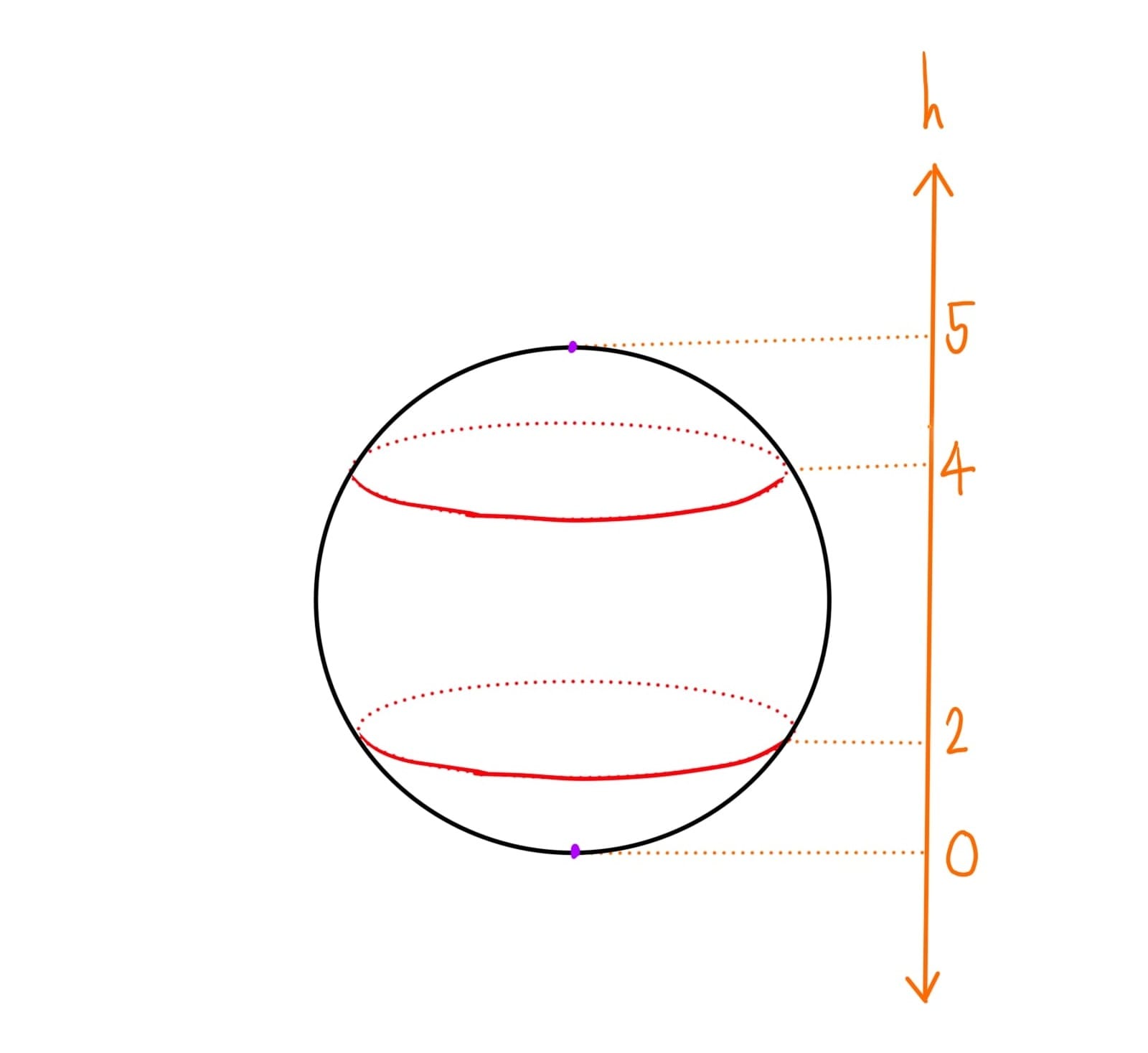
จุด → จาน → ทรงกลม
มีการเปลี่ยนแปลงทั้งหมด 2 ครั้งด้วยกัน
ทีนี้ลองเปลี่ยนภาชนะให้มีรูปทรงเหมือนเม็ดถั่ว จะเห็นรูปแบบการเปลี่ยนแปลงดังนี้
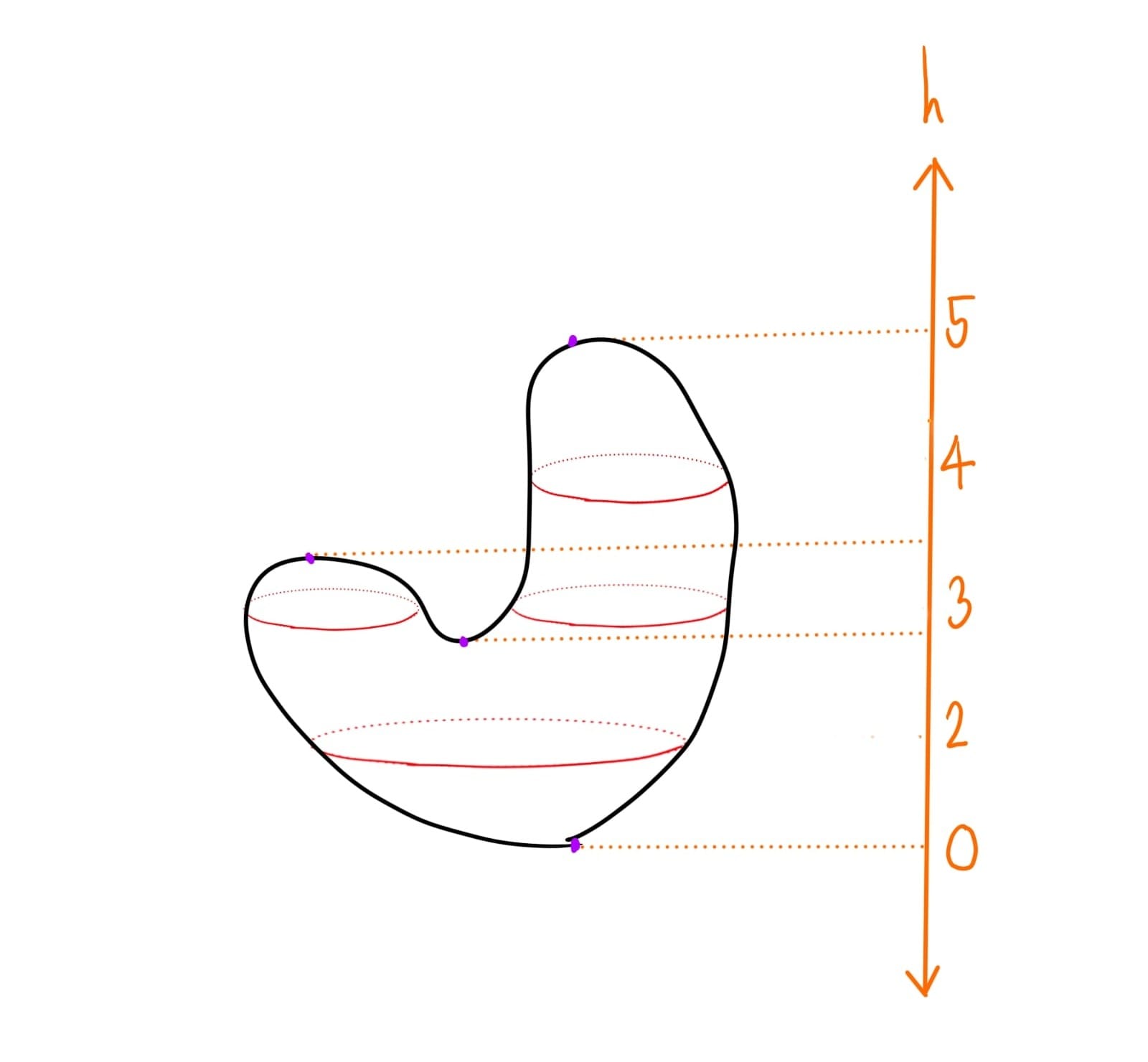
จุด → จาน → ท่อโค้ง → ท่อโค้งปลายปิดข้างนึง → ถั่ว
เป็นอีกครั้งที่มีการเปลี่ยนแปลง 4 ครั้ง แต่รูปทรง ณ แต่ละความสูงนั้นต่างกับของโดนัท
มีจุดสังเกตเล็ก ๆ นิดนึงตรงนี้คือ ถ้าเราพิจารณาแค่รอยตัด ณ ความสูงต่าง ๆ ของถั่ว เราจะได้ลำดับ จุด → วงกลม 1 วง → วงกลม 2 วง → วงกลม 1 วง → จุด ซึ่งเหมือนกับของโดนัท ความต่างของสองลำดับนี้อยู่ที่การเปลี่ยนผ่านครั้งที่สาม ซึ่งสำหรับถั่ว วงกลมวงนึงจะยุบหายไป แต่สำหรับโดนัทวงกลมทั้งสองจะกลับมารวมกัน เหตุผลก็คือจุดเปลี่ยนผ่านสองจุดนี้เป็นคนละประเภทกัน ดังที่จะอธิบายเพิ่มเติมข้างล่าง
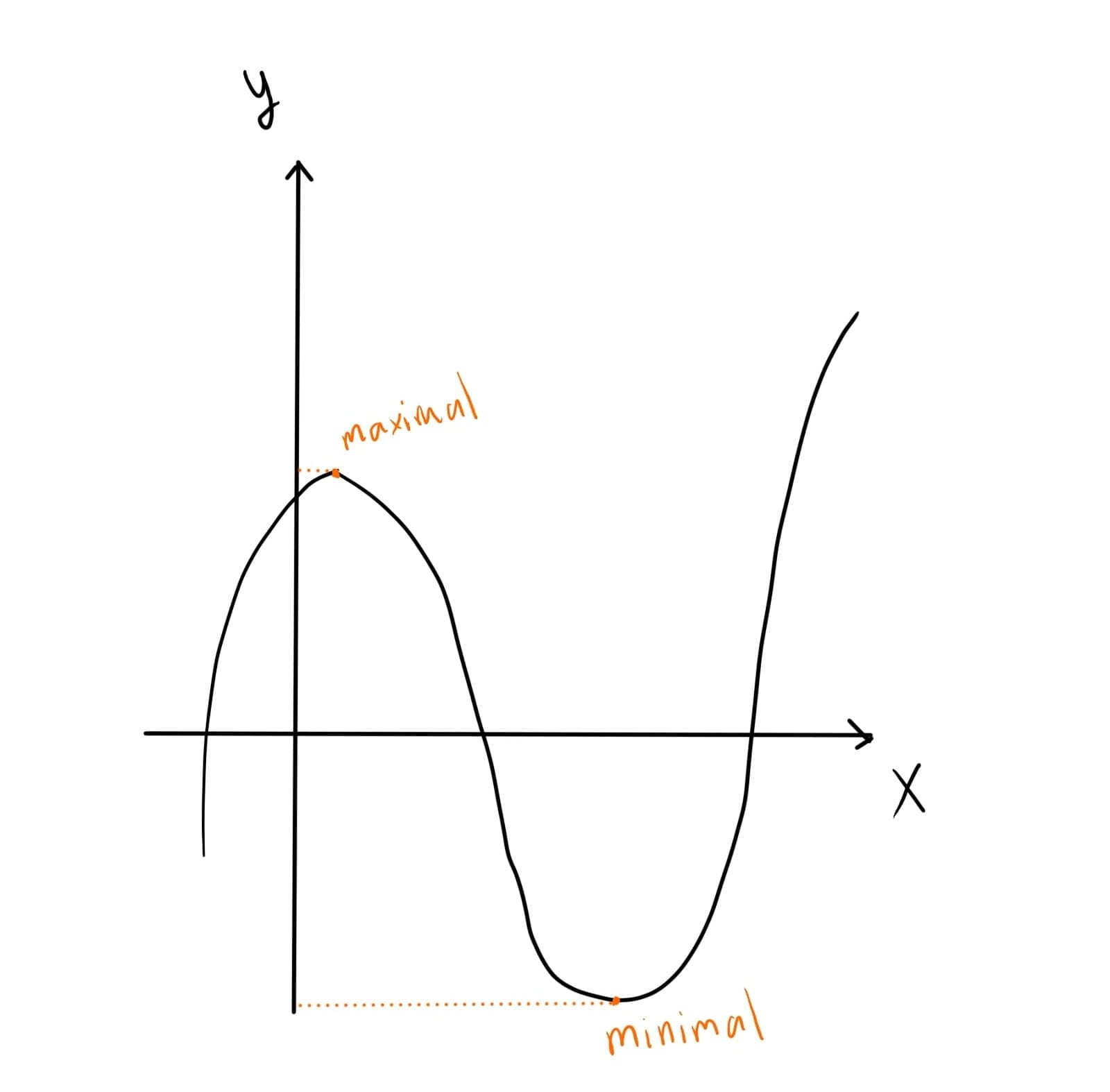
ในวิชาแคลคูลัส จะมีอยู่บทหนึ่งที่เราต้องร่างกราฟของฟังก์ชัน หลักการพื้นฐานที่สุดของการร่างกราฟก็คือเราต้องมองหา "จุดวิกฤต" ของกราฟ เพราะ "ที่จุดวิกฤต รูปร่างของกราฟจะมีการเปลี่ยนแปลง"
ทบทวนนิยามกันสักเล็กน้อย จุดวิกฤตก็คือจุดที่ค่าอนุพันธ์ หรือที่เรียกติดปากกันว่าดิฟ ของฟังก์ชันเป็นศูนย์ df/dx=0 ซึ่งจุดวิกฤตที่สังเกตง่าย ๆ ก็คือจุดต่ำสุดสัมพัทธ์ (minimal) กับจุดสูงสุดสัมพัทธ์ (maximal)
เมื่อเราเคลื่อนที่ไปตามกราฟจากซ้ายไปขวา เราจะเห็นว่ารูปร่างของกราฟเราเปลี่ยนแปลงไปเมื่อเราเคลื่อนผ่านจุดวิกฤต ใช่แล้วครับ นี่คือหลักการเดียวกับการเปลี่ยนแปลงรูปร่างของภาชนะที่เล่าไปข้างบนเลย!
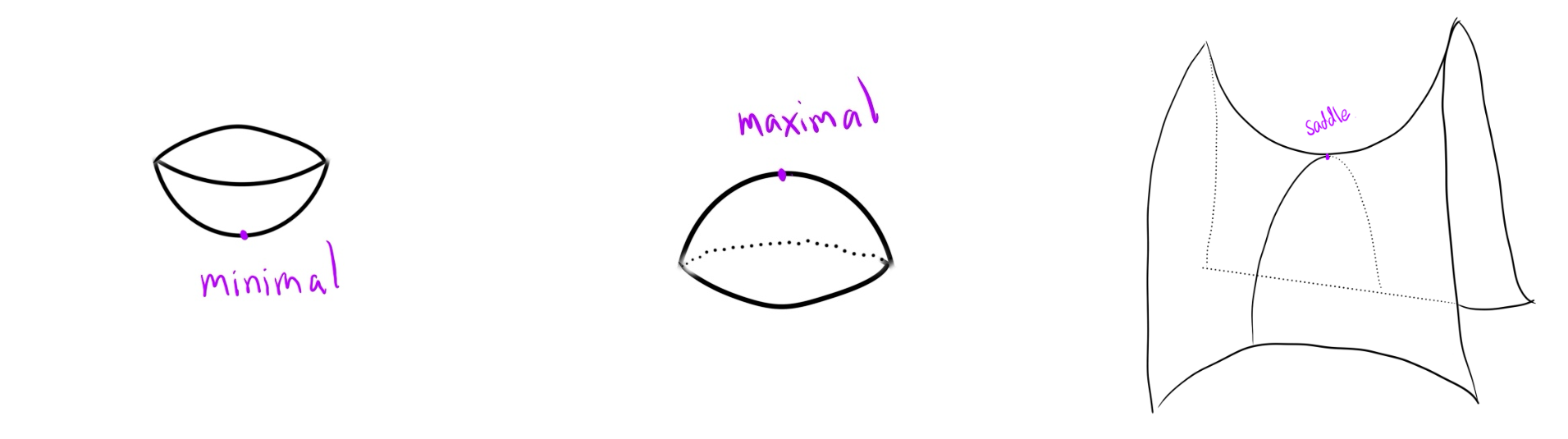
กราฟที่เราร่างกันในวิชาแคลคูลัสนั้นเป็นรูปทรงหนึ่งมิติ จึงมีจุดวิกฤตหลัก ๆ อยุ่แค่ 2 แบบดังกล่าวข้างต้น แต่เมื่อเราพิจารณาภาชนะที่มีสองมิติ จะมีจุดวิกฤตอีกประเภทหนึ่งโผล่ขึ้นมา นั่นคือ จุดอานม้า (saddle) ซึ่งเป็นจุดที่มีลักษณะเหมือนจุดต่ำสุดเมื่อมองจากทิศทางหนึ่ง แต่เมื่อมองจากอีกทิศทางมันจะดูเหมือนเป็นจุดสูงสุด
ที่นี้ลองย้อนกลับมาดูภาชนะทั้ง 3 ข้างต้นกันอีกครั้ง ขอย้ำคติพจน์กันอีกครั้ง "ทุกจุดวิกฤตมีการเปลี่ยนแปลง"
โดนัท: มีการเปลี่ยนแปลงทั้งหมด 4 ครั้ง แปลว่าโดนัทของเรามีจุดวิกฤตอยู่ 4 จุด
จุดต่ำสุดสัมพัทธ์ → จุดอานม้า → จุดอานม้า → จุดสูงสุดสัมพัทธ์
โดนัทประกอบด้วย จุดต่ำสุดสัมพัทธ์ 1 จุด จุดอานม้า 2 จุด และจุดสูงสุดสัมพัทธ์ 1 จุด ขอแทนจำนวนจุดทั้งสามประเภทนี้ด้วย A = 1, B = 2, C = 1 สังเกตเล่น ๆ ว่า A - B + C = 0
ทรงกลม: มีการเปลี่ยนแปลง 2 ครั้ง
จุดต่ำสุดสัมพัทธ์ → จุดสูงสุดสัมพัทธ์
สำหรับวงกลม A = 1, B = 0, C = 1 และ A - B + C = 2
ถั่ว: มีการเปลี่ยนแปลงทั้งหมด 4 ครั้ง
จุดต่ำสุดสัมพัทธ์ → จุดอานม้า → จุดสูงสุดสัมพัทธ์ → จุดสูงสุดสัมพัทธ์
สำหรับถั่ว A = 1, B = 1, C = 2 และ A - B + C = 2
จะเห็นว่าการเปลี่ยนแปลงของรูปทรงนั้นสัมพันธ์กับจุดวิกฤตจริง ๆ! ว่าแต่ตัวเลข A - B + C บอกอะไรกับเรา?
บางคนอาจเคยได้ยินมาว่าสำหรับนักคณิตศาสตร์กลุ่มหนึ่งที่เรียกตัวเองว่า topologist ไม่สามารถบอกความแตกต่างระหว่างโดนัทกับแก้วกาแฟ (แก้วแบบมีหู) นั่นก็เพราะในวิชา Topology รูปร่างหนึ่ง ๆ ไม่ต่างกับอีกรูปร่างหนึ่ง ถ้าเราสามารถบิดมันไป ๆ มา ๆ จนกลายร่างเป็นกันและกันได้ (โดยห้ามบิดให้มันขาดออกจากกัน)
ดังนั้นสำหรับ topologist แล้วทรงกลมกับถั่วนั้นเป็นรูปทรงเดียวกัน แต่ทั้งสองสิ่งนี้เป็นคนละรูปทรงกับโดนัท และอันที่จริงแล้วตัวเลข
A - B + C = จำนวนจุดต่ำสุดสัมพัทธ์ - จำนวนจุดอานม้า + จำนวนจุดสูงสุดสัมพัทธ์
สามารถบอกสิ่งนี้กับเราได้ !
ที่จริงแล้วรูปทรงปิดสองมิติทั้งหมดที่ไม่มีการบิดท่ายาก (ตัวอย่างของพื้นผิวปิดที่มีการบิดท่ายากคือ Klien Bottle ซึ่งเป็นขวดประหลาดที่อาศัยอยู่ในปริภูมิ 4 มิติ) นั้นสามารถจำแนกได้ด้วยการนับจำนวนรูของมัน โดนัท 0 รู (ทรงกลม) , โดนัท 1 รู, โดนัท 2 รู,...
ถ้าเราแทนจำนวนรูนี้ด้วยตัวแปร g (genus) เราจะพบว่า
A - B + C = 2 - 2g
กล่าวคือค่า A-B+C สามารถบอกจำนวนรูของรูปทรงสองมิติได้ ! อันที่จริงค่านี้ก็ยังเท่ากับค่า
Euler Characteristic = จำนวนจุด - จำนวนด้าน + จำนวนหน้า
อันโด่งดังอีกด้วย !
สำหรับใครที่ไม่เคยได้ยินเรื่อง Euler characteristic มาก่อน ก็หวังว่าผู้เขียนจะมีโอกาสได้มาเล่าให้ฟังในโอกาสต่อ ๆ ไป
และนี่ก็คือหลักการพื้นฐานของวิชา Morse Theory ซึ่งไม่เพียงสามารถใช้กับรูปทรงสองมิติ แต่ยังสามารถใช้งานได้กับรูปทรงที่มีมิติยิ่ง ๆ ขึ้นไป กล่าวคือมีมิติ n ใด ๆ โดยนักคณิตผู้เป็นต้นคิดทฤษฎีนี้ก็คือ Marston Morse (1892-1977) นักคณิตศาสตร์ชาวอเมริกันที่ J. Robert Oppenheimer ถึงกับเคยกล่าวยกย่องให้เป็นรัฐบุรุษแห่งวงการคณิตศาสตร์ Morse นำเสนอทฤษฎีนี้ขึ้นเมื่อปี 1929 และนับแต่นั้นมาทฤษฎีนี้ได้ถูกศึกษา พัฒนา และเป็นแรงบันดาลใจให้เกิดทฤษฎีใหม่ ๆ ขึ้นอีกมากมาย ไม่ว่าจะเป็น Morse-Bott Theory, Floer Cohomology, Fukaya Category และอีกมากมาย ทฤษฎีเหล่านี้ยังคงมีโจทย์ปัญหามากมายรอคอยให้นักคณิตศาสตร์รุ่นใหม่เข้ามาช่วยไข
ไม่เพียงเท่านั้น Morse Theory ยังถูกนำไปประยุกต์ใช้ในการจัดการกับ data ได้อีกด้วย เป้าหมายหลักอย่างหนึ่งของ data science คือวิเคราะห์ความซับซ้อนของชุดข้อมูล โดยวิธีหนึ่งก็คือการศึกษา "รูปร่าง" คร่าว ๆ ของข้อมูล และคณิตศาสตร์ที่ถูกนำมาใช้ศึกษารูปร่างของข้อมูลก็คือ topology จึงเกิดเป็นศาสตร์ที่เรียกว่า Topological Data Analysis โดยมี Discrete Morse Theory เป็นเครื่องมือหนึ่ง
สุดท้ายนี้ผู้เขียนคงอยากจะบอกว่า จงใช้ชีวิตไปตาม flow แล้วอย่าลืมว่า
“ทุกจุดวิกฤตมีการเปลี่ยนแปลง”
ของแถมปิดท้าย ในกรณีทั่วไป เราไม่จำเป็นต้องศึกษาแค่หน้าตัดตามระดับความสูง แต่เราสามารถศึกษาหน้าตัดของฟังก์ชัน f บนรูปทรง n มิตินั้น ๆ (ระดับความสูงก็เป็นฟังก์ชัน ฟังก์ชันหนึ่ง) ปรากฎว่าถ้าหากฟังก์ชันนี้มีจุดวิกฤตเพียงสองจุด ก็คือจุดต่ำสุดและจุดสูงสุด (เหมือนในกรณีของทรงกลมข้างต้น) เราจะสามารถพิสูจน์ได้ว่ารูปทรงนั้นจะเป็นทรงกลมใน n มิติ (แน่นอนว่าอาจจะเป็นทรงกลมเบี้ยว ๆ เพราะในมุมมองของ topology ทรงกลมจะบิด ๆ เบี้ยว ๆ ยังไงก็ได้) ทฤษฎีบทนี้มีชื่อว่า Reeb's Theorem คำอธิบายง่าย ๆ สำหรับทฤษฎีบทนี้ก็คือ รูปทรงของจุดต่ำสุดกับจุดสูงสุดนั้นดูเหมือนจานหงายกับจานคว่ำ ในเมื่อมันไม่มีจุดวิกฤตอื่นอยู่ระหว่างกลาง รูปทรงนี้ก็ต้องเป็นจานหงายประกบกับจานคว่ำ หรือก็คือทรงกลม ๆ นั่นเอง
เอกสารอ้างอิง
ถ้าสนใจเรียนรู้เกี่ยวกับ Morse theory ควรมีความรู้พื้นฐานเกี่ยวกับแมนิโฟลด์ หนังสือ textbook เกี่ยวกับ Morse theory เบื้องต้น เช่น
- A. Banyaga, D. Hurtubise, and D. Ajayi. Lectures on Morse homology. Vol. 29. Springer, 2004.
- M. Audin, M. Damian, and R. Erne. Morse theory and Floer homology. Vol. 2. Springer, 2014.