R² สูงไม่ได้แปลว่าโมเดลดีเสมอไป

ถ้าคุณเคยเรียนสถิติ หรือทำงานกับข้อมูลมาบ้าง ก็น่าจะเคยได้ยินชื่อ R² ผ่านหูกันมาบ้างใช่ไหมครับ?

R² หรือ Coefficient of Determination คือค่าทางสถิติที่นิยมใช้กันมากเวลาทำ Regression ซึ่งคือการพยายามทำนายค่าของตัวแปรบางอย่าง ด้วยตัวแปรต้นที่เรามีอยู่ในมือ

R² นั้นจะมีค่าอยู่ระหว่าง 0 ถึง 1 โดยคนมักจะตีความกันง่าย ๆ ว่า ถ้าค่า R² เข้าใกล้ 1 แปลว่าโมเดลที่เราสร้างขึ้นนั้นใช้งานได้ดี ส่วนถ้าค่า R² เข้าใกล้ 0 นั้นแปลว่าโมเดลที่เราสร้างขึ้นนั้นใช้งานได้ไม่ดีเท่าไร

แต่มันตรงไปตรงมาอย่างนั้นเลยหรือเปล่า

สมมติว่าผมมีเพื่อนอยู่คนนึงชื่อบาส บาสชอบมาสายมาก นัดทีไรเลทตลอดจนผมเบื่อจะบ่น ก็เลยคิดว่าช่างมันแล้วกัน แค่ไปให้พอดีกับเวลาที่บาสจะมาก็พอ แต่ปัญหาคือแต่ละครั้งบาสมาสายมากสายน้อยไม่เท่ากันนี่สิ

ผมเลยเกิดความคิดขึ้นมาว่า ถ้าเราพอรู้ข้อมูลเกี่ยวกับนิสัยของบาส เช่น บ้านอยู่ไกลแค่ไหน ฝนตกมั้ย หรือนัดกันช่วงเวลาไหนของวัน เราน่าจะลองสร้างโมเดล Regression ง่าย ๆ เพื่อทำนายว่าบาสจะมาสายกี่นาทีดูนะ

1. แม้ค่า R² จะสูง ก็ไม่ได้แปลว่าโมเดลของเรานั้นถูกต้องเสมอไป:

ผมเริ่มต้นจากการลองหยิบตัวแปรต้นที่เราคิดว่าน่าจะเกี่ยวกับเวลาที่บาสจะสายโดยตรง นั่นคือระยะทางจากบ้านบาสมายังสถานที่นัด

ลอง fit โมเดลที่ง่ายที่สุดนั่นคือ Linear Regression ดู ให้ระยะทางเป็นตัวแปรต้น และเวลาที่บาสสายเป็นตัวแปรตาม ปรากฎว่าได้โมเดลที่ออกมาได้ R² = 0.76 แหนะ ซึ่งถือว่าเยอะเลย งั้นก็ปิดจ็อบได้เลยไหม

แต่เมื่อผมลองเอาข้อมูลมาวาดกราฟดูจริง ๆ กลับพบว่าข้อมูลมีลักษณะเป็นแบบ exponential ไม่ใช่แบบเส้นตรงแบบที่โมเดลเราใช้

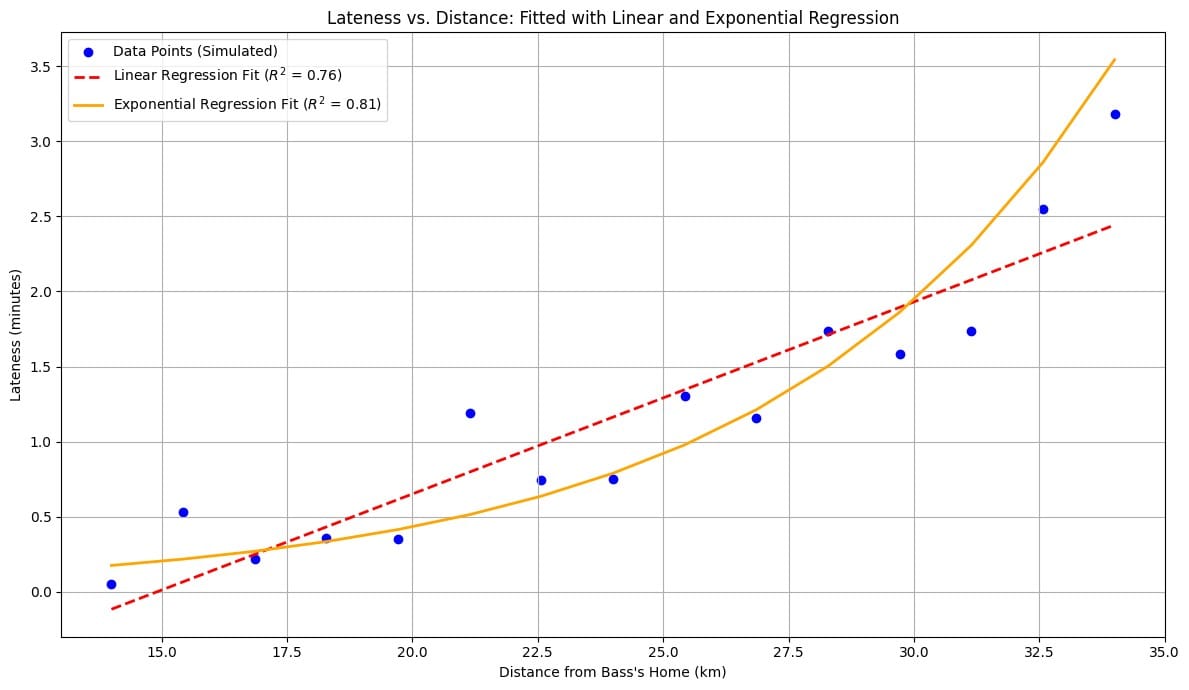
กรณีแบบนี้ทำให้เห็นว่า แม้โมเดลจะมี R² ที่สูง แต่โครงสร้างของโมเดลอาจจะไม่สอดคล้องกับธรรมชาติของข้อมูลก็ได้

2. R² ไม่ได้บอกว่า residual มีปัญหาหรือเปล่า:

หนึ่งในวิธีง่าย ๆ ที่เราเอาไว้ใช้ทดสอบว่าโมเดลของเราถูกต้องหรือไม่คือการดูเศษเหลือจากการทำนาย หรือที่เรียกว่า residual ครับ

residual คือ ค่าของส่วนต่างระหว่างค่าจากข้อมูลจริง (Actual) กับค่าที่โมเดลทำนาย (Predicted) ซึ่งตามสมมติฐานของ Linear Regression นั้น residual มันควรเป็นอิสระจากกัน ไม่มีแพทเทิร์น และมีค่าแปรปรวนคงที่

ซึ่งเมื่อเราลองเอาข้อมูลของบาสและเส้นตรงจากโมเดลมาลองวาดเป็น residual plot มาดู จะพบว่ามันมีลักษณะเป็นโค้งเหมือนตัวยู ซึ่งแปลว่ามีแพทเทิร์นที่ชัดเจน

สิ่งนี้หมายความว่าโมเดล Linear Regression ของเราอาจจะกำลังพยายามฟิตเส้นตรงกับข้อมูลที่มีความสัมพันธ์แบบเส้นโค้ง หรือที่เราเรียกว่า non-linear relationship นั่นเอง

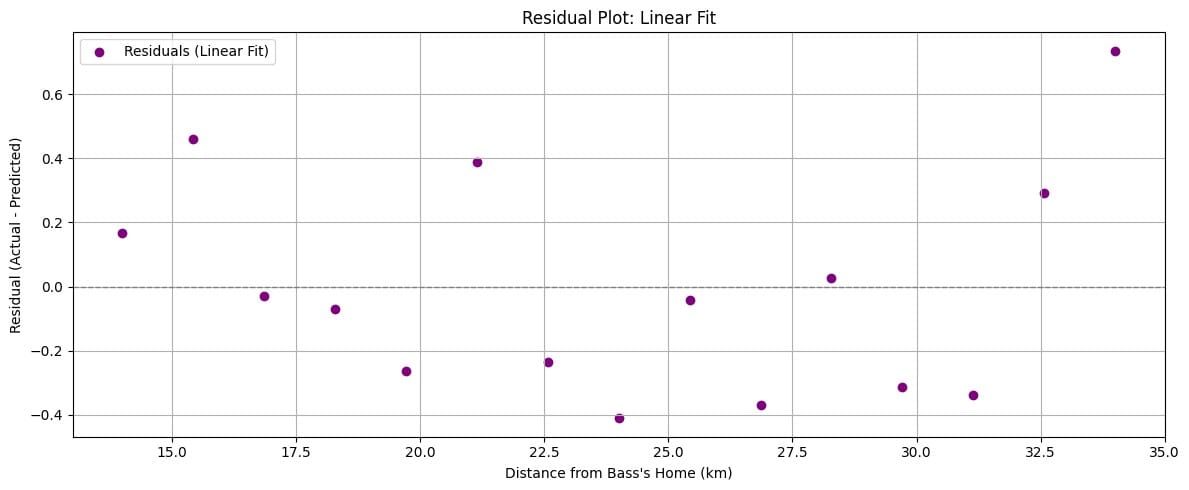
ถ้าเราสังเกตเห็นแนวโน้มบางอย่างใน residuals นั่นอาจเป็นสัญญาณว่าเรากำลังแหกสมมติฐานของการทำ Regression อยู่ ดังนั้น แม้ R² จะดูดี แต่ก็ไม่ควรพึ่งพาเพียงอย่างเดียว ควรตรวจสอบ residual plots และตรวจสอบข้อสมมติของโมเดลร่วมด้วยเสมอ

3. R² สูงได้ แม้เราจะลืมตัวแปรที่สำคัญไป:

แต่เวลามาสายของบาสนั้นขึ้นอยู่กับระยะทางแค่อย่างเดียวหรือเปล่า

ไม่น่าใช่เนอะ เพราะการมาสายของบาสอาจจะมาจากหลายปัจจัยใช่ไหมครับ ฝนตกอาจจะมีผล เวลาที่นัดก็อาจจะมีผล เวลานอนของบาสเมื่อคืนก็อาจจะมีผล และอื่น ๆ ที่ซึ่งอาจเป็นตัวแปรเกี่ยวข้อง แต่คุณไม่ได้ใส่มันลงไป

และเมื่อเราลองใช้ตัวแปรต้นเป็นตัวแปรอื่น หรือลองใส่หลาย ๆ ตัวเข้าไป เราอาจจะได้ R² ที่สูงพอ ๆ กัน หรือเผลอ ๆ อาจจะสูงกว่าด้วยก็ได้

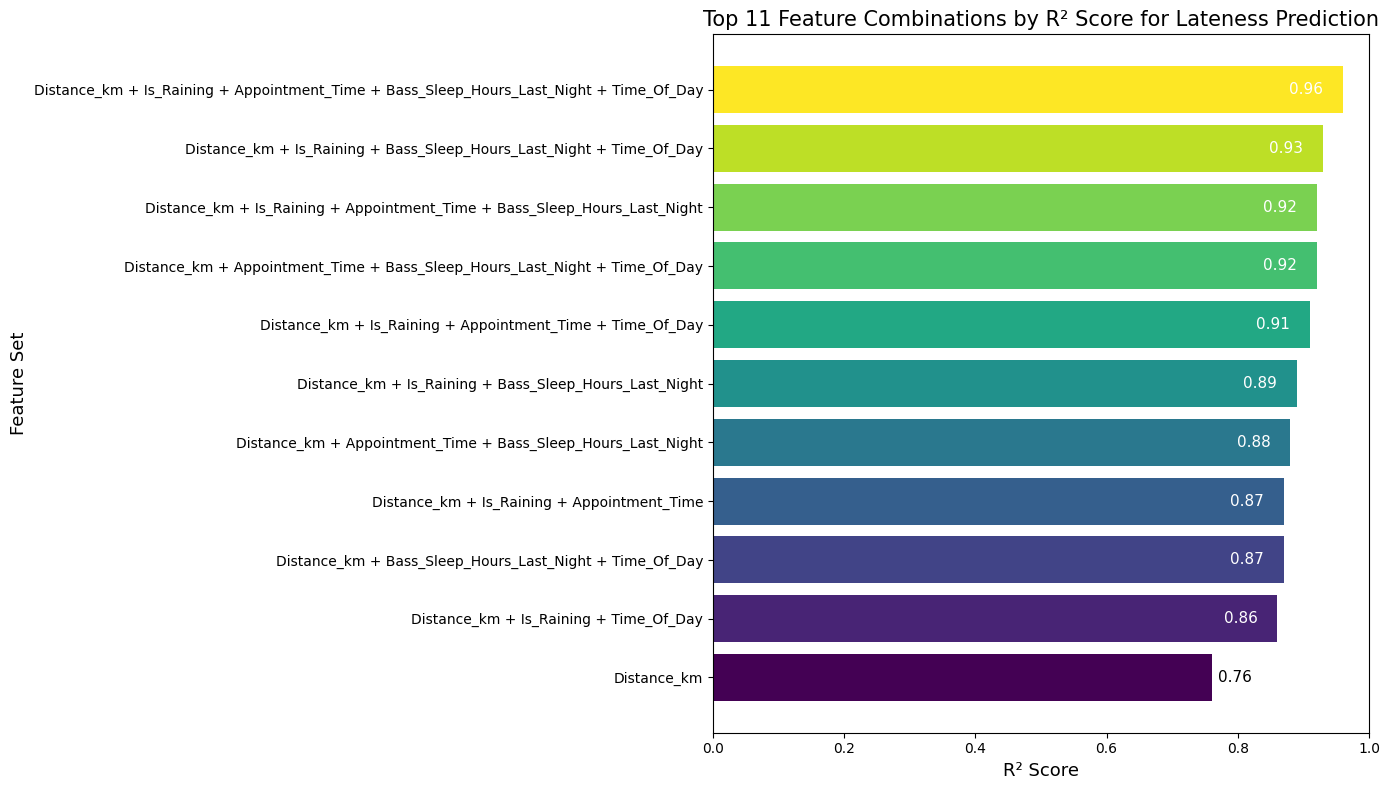
เพราะฉะนั้นเราจึงต้องพยายามเข้าใจบริบทของปัญหานั้น ๆ ด้วย ว่ามีตัวแปรอะไรบ้างที่น่าเอามาร่วมพิจารณา และอย่าตัดสินใจทุกอย่างจากแค่ R² อย่างเดียว

4. R² สูง ไม่ได้แปลว่าโมเดลทำนายได้แม่นยำเสมอไป:

หลังจากที่เราเจอปัญหาจากข้อที่แล้วที่ใช้ข้อมูลไม่ครบ คราวนี้เราเลยยัดข้อมูลทุกอย่างที่มีเข้ามาในโมเดลให้หมดเลย

และเมื่อเราลองนำไป fit กับข้อมูล โมเดลก็ให้ค่า R² ที่สูงมากถึง 0.96 กลับมา

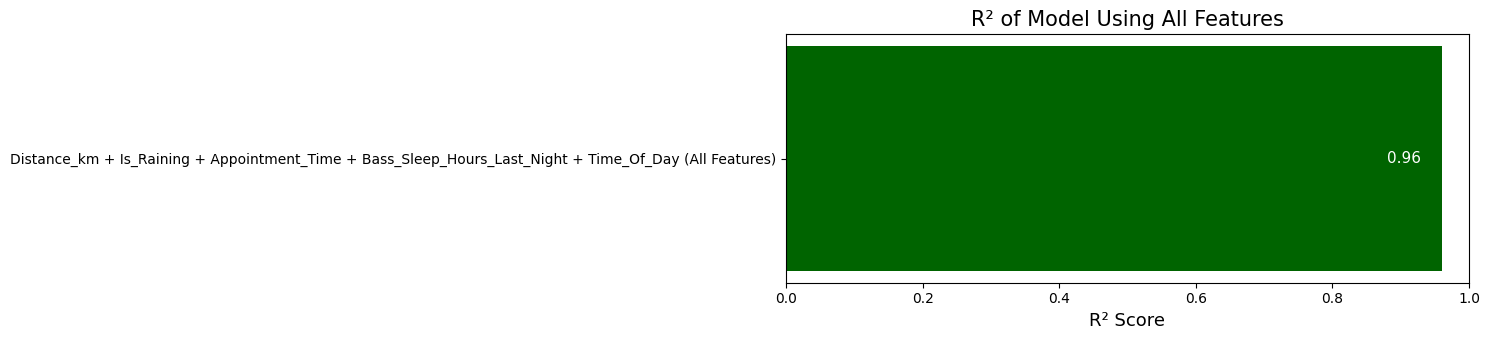
เราก็ดีใจกันยกใหญ่ คิดว่าคงจะไม่เกิดปัญหาอะไรอีกแล้ว และโมเดลก็คงจะโคตรจะแม่นแน่นอน แต่พอครั้งต่อมาที่เรานัดเจอบาสและลองใช้โมเดลนี้ในการทำนาย ผลลัพธ์ที่ได้มากลับพังไม่เป็นท่า คิดว่าจะเลทแค่ 5 นาที สุดท้ายเลทจริงไปตั้ง 40 นาที

เราก็เกาหัวแกร่ก ๆ ว่ามันจะเป็นแบบนั้นไปได้ยังไง โมเดลเราได้ R² สูงตั้ง 0.96 เลยนะ

สิ่งนี้อาจเกิดจากสถานการณ์ที่เรียกว่าการ Overfitting หรือก็คือการที่โมเดลถูกทำให้ใช้ได้ดีกับข้อมูลเก่าที่ใช้สร้างโมเดลมากเกินไป จนพอไปเจอข้อมูลใหม่ในหน้างานจริงแล้วมันกลับทายไม่ถูกซะอย่างนั้น

ปัญหานี้ก็มีวิธีแก้อยู่หลายวิธี อย่างเช่นการเลือกใช้แค่ตัวแปรต้นที่สำคัญจริง ๆ หรือการใช้ค่าอื่นมาช่วยตรวจสอบด้วย เช่น Adjusted R² หรือแยกข้อมูลเป็น train set กับ test set ก่อนแล้วหาค่า Cross-validation score เป็นต้น

5. R² ไม่ได้บอกเรื่อง causality:

ข้อสุดท้ายที่สำคัญที่สุด ค่า R² บอกแค่ว่าสองตัวแปรมี correlation หรือสัมพันธ์กัน แต่ไม่ได้อะไรเป็นต้นเหตุของอะไรเสียหน่อย

เช่นถ้าโมเดลของเราดันพบว่าตัวแปรต้น 'การแต่งตัวง่าย ๆ' ของบาสวันนั้นให้ค่า R² ที่สูงมากกับการมาสาย หลายคนอาจจะเผลอสรุปไปว่า “อ๋อ เพราะวันนี้บาสแต่งตัวง่าย ๆ ไงเลยมาสาย” ซึ่งฟังดูแปลกมาก

ทั้งที่จริงแล้วมันอาจจะเพราะว่าวันนั้นบาสตื่นสายเลยต้องแต่งตัวง่าย ๆ แค่นั้นเอง คือทั้งการแต่งตัวง่าย ๆ และการมาสายนั้นเป็นผลของการตื่นสายเฉย ๆ

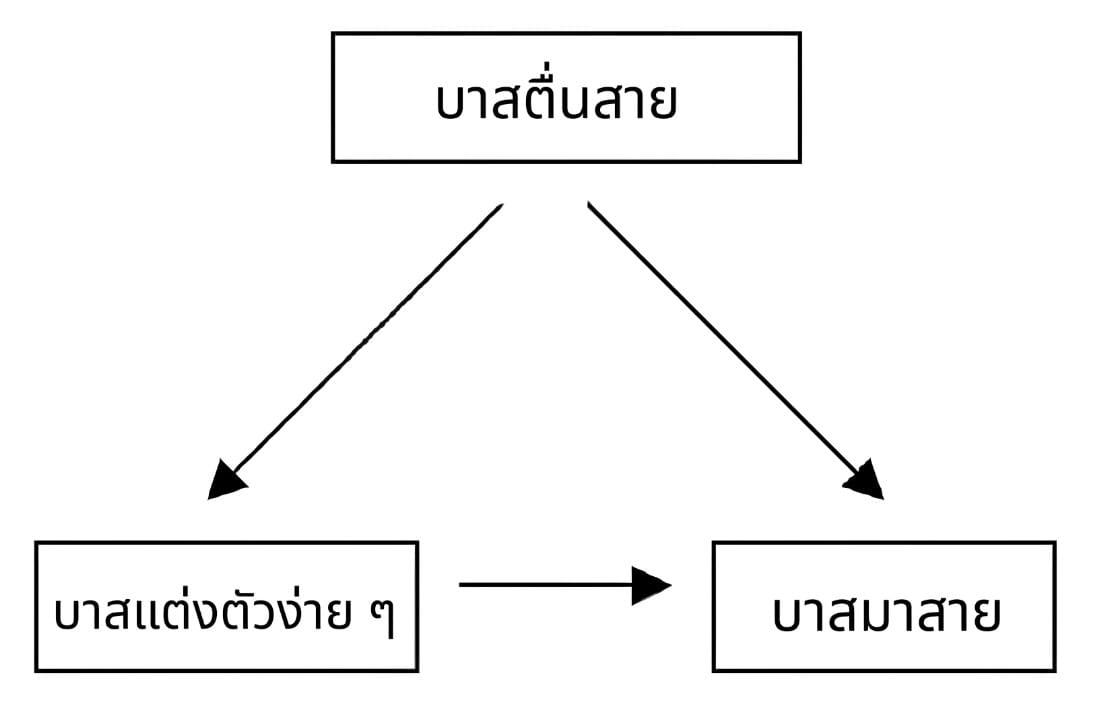
การตื่นสายอาจเป็น "สาเหตุแท้จริง" ร่วมกันที่ส่งผลต่อทั้งสองตัวแปรครับ เราไม่สามารถด่วนสรุปว่า "เพราะสิ่งนี้เลยทำให้เกิดสิ่งนั้น" จากการที่เราดูแค่ค่า R²

ทั้งหมดนี้คือสิ่งที่ R² ไม่สามารถบอกได้ แล้วจริง ๆ แล้ว R² บอกอะไร?

ในเชิงคณิตศาสตร์นั้น R² นั้นคือ สัดส่วนของความแปรปรวนในตัวแปรตาม ที่สามารถอธิบายได้ด้วยตัวแปรอิสระต้นที่อยู่ในโมเดล หรือเขียนเป็นสูตรได้ว่า

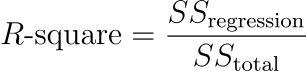
ค่า R² ที่สูงบ่งบอกว่าโมเดลสามารถอธิบายความแปรปรวนของข้อมูลได้ดี แต่ไม่ได้หมายความว่าโมเดลจะทำนายได้แม่นยำ โครงสร้างจะถูกต้อง หรือใช้ตัวแปรครบถ้วน และที่สำคัญ R² ไม่สามารถบอกเหตุและผลของความสัมพันธ์ระหว่างตัวแปรได้เลย

เพราะฉะนั้น ถ้าจะประเมินคุณภาพของโมเดล เราควรดูมากกว่าแค่ R² ครับ เราควรต้องพิจารณาปัจจัยอื่นๆ ควบคู่กัน เช่น บริบทของปัญหา เป้าหมายของการทำโมเดล สมมติฐานของโมเดลที่เลือกใช้ และพิจาณาค่าทางสถิติอื่น ๆ ประกอบด้วย ไม่ว่าจะเป็น การวิเคราะห์ Residuals หรือ Metrices ตัวอื่น ๆ เช่น Adjusted R² ค่า Cross-validation score ค่า p-values และอื่น ๆ อีกมากมาย

เพราะ R² ก็เหมือนเครื่องมือทางสถิติอื่น ๆ คือมีทั้งจุดแข็งและข้อจำกัด

ซึ่งการที่เราเข้าใจถึงข้อจำกัดของมัน จะช่วยให้เราสามารถตีความมันได้อย่างถูกต้อง สร้างโมเดลที่มีประสิทธิภาพ และสามารถนำไปใช้กับเคสจริงได้ดีมากยิ่งขึ้นครับ

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง

https://statisticsbyjim.com/regression/interpret-r-squared-regression/
https://getrecast.com/r-squared/
https://medium.com/@TisanaWanwarn/why-we-cannot-trust-r-squared-567532ccd021
https://library.virginia.edu/data/articles/is-r-squared-useless
https://www.tandfonline.com/doi/full/10.1080/15140326.2023.2207326