ทำไม WeVis ถึงเลือกใช้ Jensen–Shannon Divergence

ผมเป็นแฟนคลับ WeVis ครับ

เขามักจะเอาข้อมูลทางการเมืองมาเล่าอย่างน่าสนใจอยู่เสมอ โดยเฉพาะช่วงใกล้เลือกตั้งแบบนี้ รวมถึงโพสท์ล่าสุดที่ลองเอาคะแนนเลือกตั้งปี 66 แบบบัญชีรายชื่อและแบบแบ่งเขตมาเทียบกัน เพื่อดูว่าแต่ละเขตเลือกสองใบเหมือนกัน หรือแตกต่างกันมากน้อยแค่ไหน

แว้บแรกที่ผมอ่าน ผมคิดว่า เห้ย น่าสนใจแฮะ เพราะตอนปี 66 นั้นมีปรากฎการณ์เลือกสองใบคนละสีให้เห็นอยู่หลายเขต ส่วนแว้บที่สอง ผมนึกสงสัยขึ้นมาว่า แล้วเขาวัด 'ความแตกต่าง' ที่ว่านั้นยังไงนะ

จนเหลือบไปเห็นดอกจันตรงมุมขวาล่าง ว่าเขาคำนวณด้วย Jensen-Shannon Divergence นั่นเอง แล้วก็ได้แต่คิดว่า WeVis นี่ไม่ทำให้ผิดหวังจริง ๆ

คืออย่างนี้ฮะ เราต้องเข้าใจก่อนว่า สิ่งที่ WeVis กำลังพยายามวัดอยู่นั้นคือความต่างระหว่างอัตราส่วนคนที่กาบัตรให้แต่ละพรรคระหว่างบัตรสองใบ

เช่น ในเขตเลือกตั้งแห่งหนึ่ง สมมติว่ามีสามพรรค A B C ได้คะแนนแบบบัญชีรายชื่อเท่ากับเป็นอัตราส่วน 50% 20% และ 30% แต่ได้คะแนนแบบแบ่งเขตเท่ากับ 10% 55% และ 35% ซึ่งแตกต่างกันอย่างชัดเจน

คือถ้ามองแบบบัญชีรายชื่อ เขตนี้จะเป็นเขตของพรรค A แต่ถ้ามองแบบแบ่งเขต เขตนี้จะเป็นของพรรค B

แต่คำถามคือ แล้วเราจะวัดความแตกต่างระหว่างการลงคะแนนสองแบบนี้ออกมาเป็นตัวเลขสักตัวอย่างไร

วิธีที่ตรงไปตรงมาที่สุด นั่นคือมองคะแนนแต่ละแบบเป็นเวกเตอร์ นั่นคือ P = [0.5 0.2 0.3] และ Q = [0.1 0.55 0.35] และหาระยะห่างระหว่างเวกเตอร์สองอันนี้ นั่นคือ

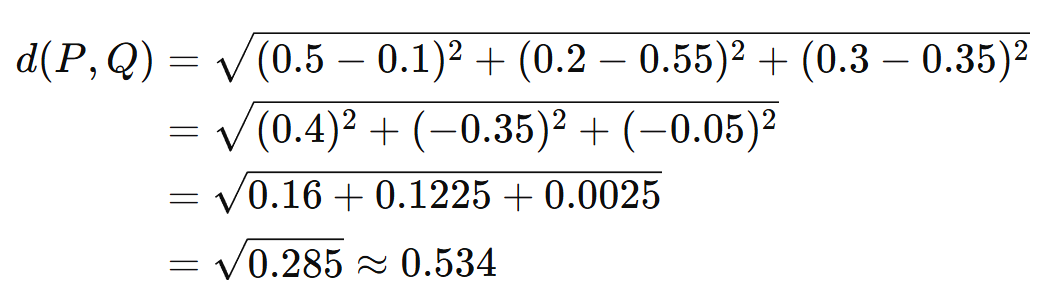
การหาระยะห่างของเวกเตอร์ด้วยวิธีนี้เรียกว่า Euclidean distance หรือระยะห่างแบบยูคลิด ซึ่งไอเดียคือการหาว่าคะแนนของแต่ละพรรคต่างกันเท่าไร แล้วเอาความต่างของทุกพรรคมารวมกัน ส่วนการยกกำลังสองและถอดรูทนั้นเพื่อไม่ให้ผลต่างออกมาติดลบนั่นเอง

Euclidean distance ก็เป็นเครื่องมือวัดความแตกต่างที่ดี แต่ปัญหาของมันคือ มันมองทุกอย่างจากมุมผลต่าง ซึ่งในทางปฏิบัติอาจจะไม่ตรงกับความรู้สึกของเรานัก ลองนึกภาพว่าพรรคใหญ่ที่ปกติได้ 95% คะแนนลดไปเหลือ 90% กับพรรคที่เคยได้ 5% คะแนนเพิ่มขึ้นมาเป็น 10%

มันก็ห่างกัน 5% เท่ากัน แต่อันแรกดูน่าตื่นเต้นน้อยกว่าเยอะ และนั่นคือสิ่งที่ Euclidean distance ไม่ได้บอกเราฮะ

สมมติเขตเลือกตั้งอีกแห่งหนึ่ง มีสามพรรค A B C เหมือนเดิม ได้คะแนนแบบบัญชีรายชื่อเท่ากับเป็นเท่ากับ 90% 10% และ 0% นั่นคือพรรค C ไม่ได้คะแนนบัตรใบแรกเลย

คราวนี้เราพิจารณาคะแนนแบบแบ่งเขตในสองกรณี กรณีแรกได้ 80% 20% 0% นั่นคือพรรค C ไม่ได้คะแนนเหมือนเดิม แต่คะแนนมีการถ่ายมาที่พรรค B

กับกรณีที่สอง คือคะแนนแบบแบ่งเขตเป็น 80% 10% 10% นั่นคือคะแนนของพรรค A ที่ลดนั้นถูกถ่ายไปที่พรรค C ซึ่งไม่ได้สักคะแนนบัตรใบแรก

สองกรณีนี้ถ้าลองเอาไปคำนวณ Euclidean distance ดู จะพบว่าได้เท่ากับ 0.1414 ทั้งคู่ นั่นคือสองสถานการณ์นี้ดูเหมือนกันทุกประการ ทั้งที่จริงแล้วบางคนอาจมองได้ว่า สถานการณ์หลังนั้นดูเป็นการเปลี่ยนแปลงเชิงโครงสร้างที่มากกว่า เพราะมันไม่ใช่แค่การถ่ายคะแนนมาให้อีกพรรคทั่ว ๆ ไป แต่มันคือการถ่ายคะแนนไปให้พรรคที่บัตรใบแรกไม่มีคะแนนด้วยซ้ำ

คำถามคือ เราจะสามารถสร้างวิธีการวัดความแตกต่างที่สามารถแยกสองกรณีที่ต่างกันนี้ออกจากกันได้ไหม และคำตอบก็คือ Jensen-Shannon Divergence นั่นเอง

สำหรับกรณีสามพรรค สูตร Jensen-Shannon Divergence เขียนได้ว่า

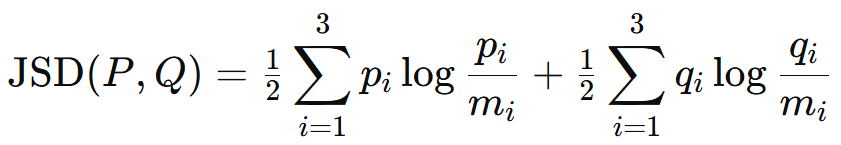
เมื่อ

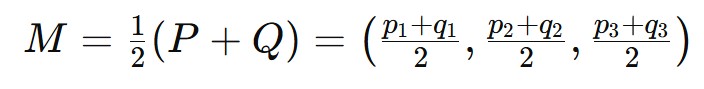
ซึ่งเพื่อไม่ให้บทความนี้อ่านยากเกินไปมากกว่านี้ ผมจึงจะไม่ลงรายละเอียดของสูตรมาก แต่เอาเป็นว่า ไอเดียหลักของมันคือการเปลี่ยนการวัดความต่างด้วย 'ผลต่าง' แบบที่ Euclidean distance ทำ ไปเป็นการวัดอัตราส่วนของความเปลี่ยนแปลง ซึ่งสอดคล้องกับความรู้สึกของมนุษย์ที่วัดต่าง ๆ เป็นจำนวนเท่ามากกว่าแบบผลต่างนั่นเอง

สำหรับสถานการณ์ที่เราคุยกันล่าสุด ถ้า P = [0.9 0.1 0.0] Q1 = [0.8 0.2 0.0] และ
Q2 = [0.8 0.1 0.1] เราจะได้ว่า ED(P,Q1) เท่ากับ ED(P,Q2)

แต่ได้ JSD(P,Q1) = 0.0100 ซึ่งน้อยกว่า JSD(P,Q2) = 0.0361 ตรงตามความรู้สึกของเรา

ด้วยเหตุนี้ Jensen-Shannon Divergence จึงเป็นวิธีการวัดความแตกต่างของการกระจายของอัตราส่วนที่นิยมใช้กันมากกว่า ถ้าคุณลองไปเสิร์ชหรือถาม AI ว่าถ้าจะวัดความแตกต่างของการกระจายอัตราส่วนควรใช้อะไรดี Jensen-Shannon Divergence ก็จะโผล่ขึ้นมาให้เห็นเป็นอันดับแรก ๆ

โอเค คุณอาจจะบอกว่า ไหนว่าดีไง ทำไม ChatGPT ถึงแนะนำเป็นอันดับ 3 แหนะ

คำตอบคือ เพราะไอ้เจ้าสองตัวแรกที่มันแนะนำมาน่ะ ใช้งานไม่ได้กับปัญหาการวัดความต่างของคะแนนระหว่างบัตรสองใบที่เรากำลังคุยกันอยู่ไงล่ะ

แต่ทำไมถึงใช้ไม่ได้ ผมทิ้งไว้เป็นการบ้านแล้วกันนะฮะ

อย่างที่ผมบอกเสมอฮะ ว่าคณิตศาสตร์นั้นไม่ใช่เรื่องของการคำนวณให้ถูกตามที่ถูกกำหนดมา เพราะถ้ามีใครมาบอกให้ผมคำนวณความแตกต่างของคะแนนระหว่างบัตรสองใบด้วย Euclidean distance หรือ Kolmogorov–Smirnov ผมก็คงตอบเขากลับไปว่า

พี่เปลี่ยนไปใช้ Jensen-Shannon Divergence เหอะ