เราคาดหวังอะไรจากตัวแปรสุ่มที่ไม่มีค่าคาดหวังได้บ้าง

ในห้องเรียนวิชาสถิติ มีทฤษฎีบทที่สำคัญอยู่สองข้อที่ทุกคนน่าจะเคยได้ยิน นั่นคือ Law of Large Numbers และ Central Limit Theorem ที่บอกว่า

Law of Large Numbers: สำหรับ X₁, X₂, …, X_n ซึ่งเป็นข้อมูลที่สุ่มมาอย่างอิสระและ มีการแจกแจงเดียวกัน (i.i.d.) ที่มีค่าคาดหวังจำกัด μ=E[X_i] เราจะได้ว่าค่าเฉลี่ยตัวอย่างจะลู่เข้าสู่ค่า μ เมื่อ n มีลู่เข้าสู่อนันต์

Central Limit Theorem: สำหรับ X₁, X₂, …, X_n ซึ่งเป็นข้อมูลที่สุ่มมาอย่างอิสระและ มีการแจกแจงเดียวกัน (i.i.d.) ที่มีค่าคาดหวังจำกัด μ=E[X_i] และมีความแปรปรวนจำกัด σ² = Var(X_i​) เราจะได้ว่าค่าเฉลี่ยตัวอย่างจะมีการแจกแจงลู่เข้าการแจกแจงปกติที่ค่าคาดหวัง μ และความแปรปรวน σ²/n เมื่อ n มีลู่เข้าสู่อนันต์

ซึ่งจะเห็นว่า ทั้งสองทฤษฎีบทนั้นมีเงื่อนไขอยู่ข้อนึงว่า ตัวแปรสุ่มต้อง "มีค่าคาดหวังจำกัด"

คำถามคือ แล้วมันมีตัวแปรสุ่มค่าคาดหวังเป็นอนันต์ด้วยหรือ หรือว่ามีตัวแปรสุ่มที่ไม่มีค่าคาดหวังด้วย ไม่ใช่ว่าคาดค่าหวังของตัวแปรสุ่มก็ต้องมีค่าจำกัดอยู่แล้วหรอกหรือ

คำตอบก็คือ มีครับ มีตัวแปรสุ่มที่มีค่าคาดหวังเป็นอนันต์ หรือไม่มีค่าคาดหวังเลยอยู่จริง ๆ แต่ก่อนจะไปถึงตรงนั้น เราทบทวนความหมายของคำว่าคาดหวังกันก่อนดีกว่า

ค่าคาดหวัง หรือ expected value ของตัวแปรสุ่ม X นั้น พูดแบบคร่าว ๆ มันคือค่าเฉลี่ยของตัวแปรสุ่มที่ถูกถ่วงน้ำหนักด้วยความน่าจะเป็น หรือเขียนเป็นภาษาคณิตศาสตร์ว่า

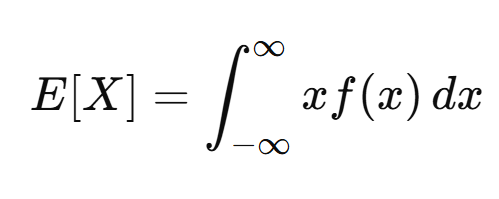
โดยจาก Law of Large Numbers เราสามารถตีความค่าคาดหวังว่าเป็น ค่าเฉลี่ยระยะยาว หรือ long-term mean ของตัวแปรสุ่ม ที่แปลว่า ถ้าเราสุ่มจากตัวแปรสุ่ม X ไปจำนวนมาก ๆ
ครั้ง ค่าเฉลี่ยของผลลัพธ์ที่ได้จากการทดลองเหล่านั้นจะเข้าใกล้ค่าคาดหวัง E[X] ของมันนั่นเอง

ดังนั้นค่าคาดหวังของตัวแปรสุ่มจะมีค่าจำกัด เป็นอนันต์ หรือไม่มีเลยนั้นก็ขึ้นอยู่กับค่าอินทิกรัลไม่จำกัดเขตในสูตร ว่าจะออกมาเป็นแบบไหน

สำหรับตัวแปรสุ่มส่วนใหญ่ที่เราคุ้นเคยนั้น เมื่ออินทิเกรตหา E[X] ออกมา มันก็จะได้เป็นตัวเลขสักค่า กรณีแบบนั้นไม่มีปัญหาอะไร ก็คือมีค่าคาดหวังจำกัดตามปกติ แต่ถ้าลองมาดูตัวแปรสุ่ม X ที่มีฟังก์ชันความหนาแน่นความน่าจะเป็นดังนี้

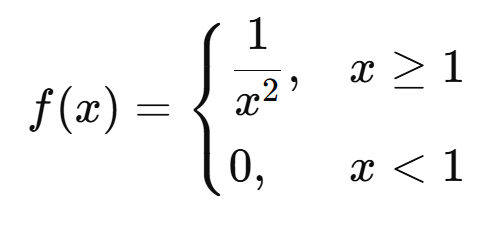
ลองเอามาหา E[X] ตามนิยามดู จะได้

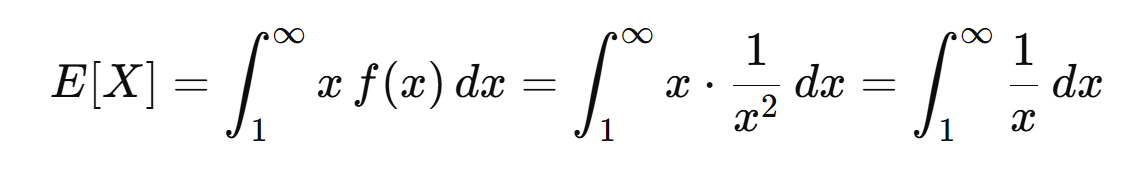
ซึ่งลู่ออกหาอนันต์ นั่นแปลว่าค่าคาดหวังของตัวแปรสุ่มที่ว่านี้มีค่าเป็นอนันต์นั่นเอง

ทีนี้เรามาลองดูตัวแปรสุ่มตัวนึงที่ชื่อว่าตัวแปรสุ่ม Cauchy ซึ่งมีฟังก์ชันความหนาแน่นความน่าหน้าตาแบบนี้

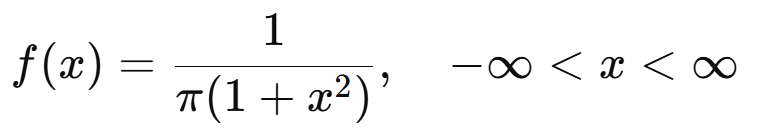
ลองเอาไปคำนวณค่าคาดหวัง จะได้ว่า

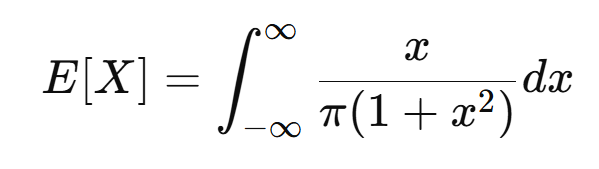
นั้นเป็นอินทิกรัลที่ลู่ออกอีกแล้ว คราวนี้ไม่ใช่การลู่ออกที่ได้อนันต์หรือลบอนันต์ด้วย ซึ่งแปลว่าตัวแปรสุ่มนี้นั้นไม่มีค่าคาดหวังนั่นเอง

คำอธิบายที่เห็นภาพหน่อยว่าทำไมตัวแปรสุ่ม Cauchy ถึงไม่มีค่าคาดหวังก็คือมันเป็นตัวแปรสุ่มที่หางที่หนักหรือ heavy tails ลองดูจากกราฟข้างล่างก็ได้ แม้ว่าหางของฟังก์ชันความหนาแน่นความน่าจะเป็นของทั้ง Normal และ Cauchy นั้นจะลู่เข้าสู่ 0 ทั้งสองข้าง แต่ของ Normal นั้นลู่เข้าเร็วกว่ามาก ในขณะที่ของ Cauchy นั้นช้า จนทำให้เมื่อคูณ x แล้วหาค่าอินทิกรัลออกมาจึงไม่ลู่เข้าหาค่าคงที่อะไรเลย

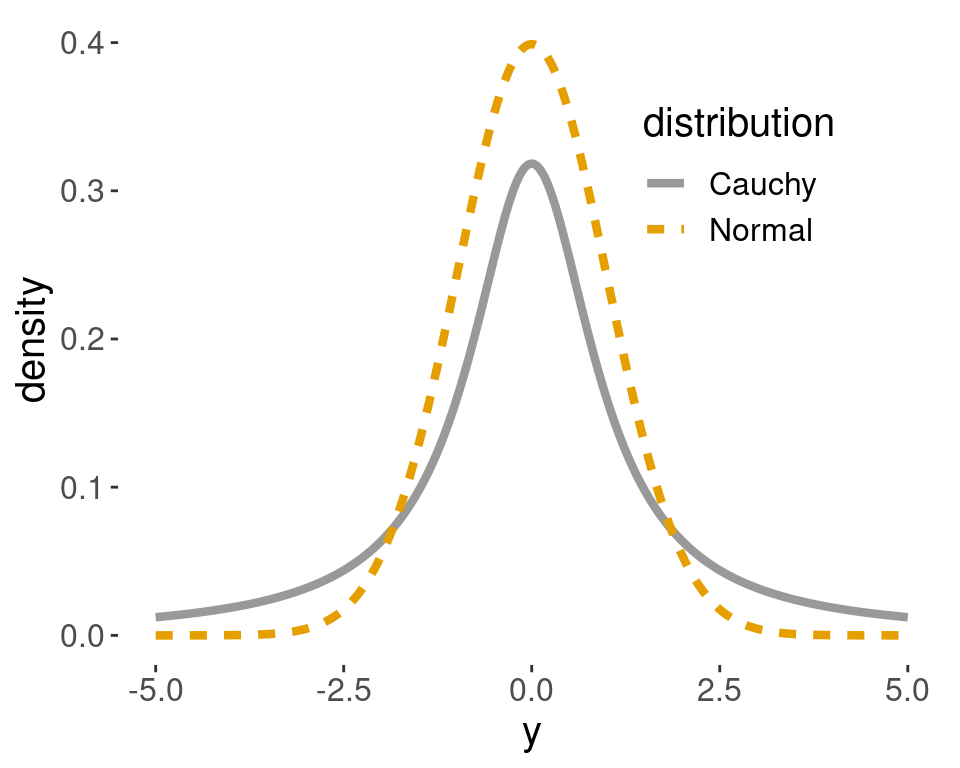
และด้วยความที่ตัวแปรสุ่ม Cauchy ไม่มีค่าคาดหวัง มันจึงไม่สอดคล้องกับเงื่อนไขของทฤษฎีบทสองข้อที่ผมยกขึ้นมาตอนต้น

สำหรับ Law of Large Numbers นั้น เราได้ว่า ค่าเฉลี่ยตัวอย่างของตัวแปรสุ่ม Cauchy นั้นไม่ได้ลู่เข้าไปหาค่าใด ๆ เลย แม้จำนวนตัวอย่าง n จะมากแค่ไหนก็ตาม ค่าที่ได้จะแกว่งไปมาอย่างไม่เสถียร ดังที่เห็นได้ในกราฟข้างล่าง แถมเรายังพิสูจน์ได้ด้วยว่าค่าเฉลี่ยตัวอย่างนี้ยังคงมีการแจกแจงแบบ Cauchy เหมือนกับตัวข้อมูลเองด้วย

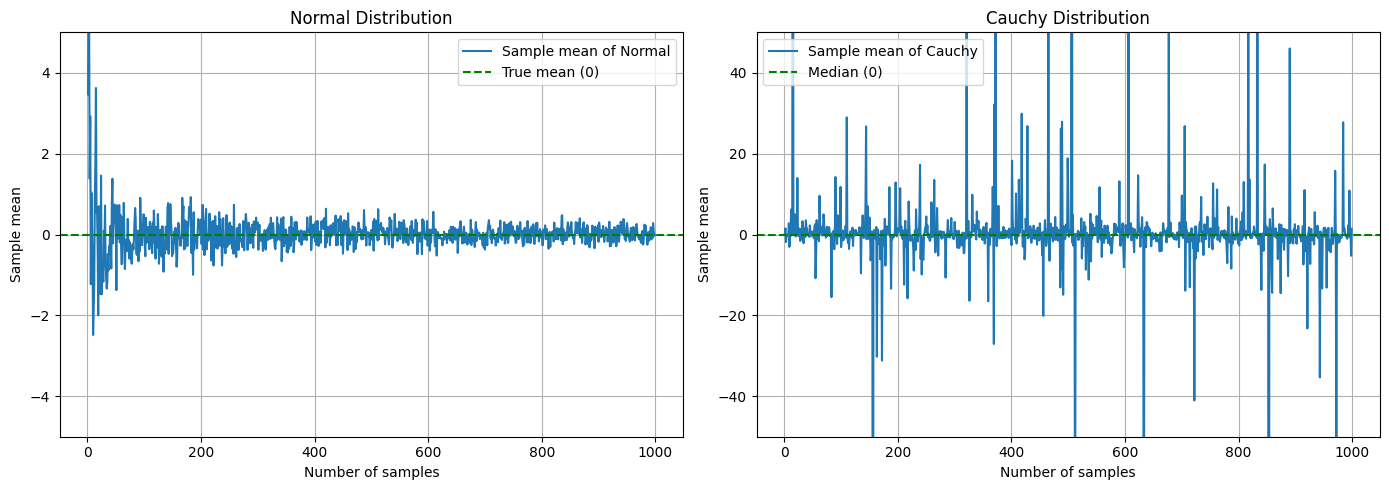
ส่วน Central Limit Theorem นั้นไม่ต้องพูดถึงเลย เพราะเนื่องจากไม่มีค่าคาดหวังและความแปรปรวนตัวแต่แรก จึงพูด Central Limit Theorem ไม่ได้ด้วยซ้ำ

เรื่องนี้ช่วยเตือนเราว่า เวลาอ่านทฤษฎีอะไรในทางคณิตศาสตร์นั้นเราต้องอ่านเงื่อนไขการใช้ให้ดี เพราะหลายคนมักจะจำ Law of Large Numbers อย่างคร่าว ๆ แค่เพียงว่า

“ค่าเฉลี่ยของตัวอย่างจะลู่เข้าค่าคาดหวังของตัวแปรสุ่มเสมอ”

แต่บทความนี้ก็แสดงให้เห็นแล้วว่าไม่ได้เป็นเช่นนั้นเสมอไป มันก็มีเงื่อนไขการใช้งานของมันอยู่ เหมือนกับทฤษฎีบทอื่น ๆ ทั้งหลายในคณิตศาสตร์นั่นแหละฮะ

ในทางปฏิบัติ เวลาพูดคุยกัน เราอาจละบางเงื่อนไขไว้บ้างเพื่อให้สื่อสารง่าย ไม่ต้องพูดทุกอย่างให้ยุ่งยาก ซึ่งจริง ๆ ก็ไม่เป็นปัญหาเลย ตราบใดที่ทั้งคนพูดและคนฟังรู้ว่ากำลังละอะไรไว้บ้าง แต่ปัญหาจะเริ่มขึ้นเมื่อเราละเงื่อนไขบ่อยเข้า จนเผลอลืมไปว่าที่จริงแล้วทฤษฎีนั้นจะจริงบนเงื่อนไขอะไรบ้างนั่นแหละฮะ

---

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

แหล่งอ้างอิง
https://www.itl.nist.gov/div898/handbook/eda/section3/eda3663.htm
https://stats.libretexts.org/Bookshelves/Probability_Theory/Probability_Mathematical_Statistics_and_Stochastic_Processes_(Siegrist)/05%3A_Special_Distributions/5.32%3A_The_Cauchy_Distribution
https://rpubs.com/mutuelinvestor/586030