ทำไมนักเดินเรือในยุคแห่งการสำรวจจึงไม่เลือกใช้เส้นทางที่สั้นที่สุด

บทความนี้เผยแพร่ครั้งแรกที่ วารสารวิทยาศาสตร์ ปีที่ 79 พ.ศ. 2568 ฉบับที่ 2 เมษายน-มิถุนายน

ใครที่ติดตามเพจ ‘คณิตศาสตร์อย่างที่ควรจะเป็น’ ของผมมาตั้งแต่ช่วงต้น ๆ อาจจะพอจำโพสท์หนึ่งได้ ตอนนั้นผมตั้งคำถามว่า “ทำไมเครื่องบินถึงไม่บินเป็นเส้นตรง”

คำถามนี้เกิดขึ้นกับตัวผมเองเมื่อตอนที่มีโอกาสได้นั่งเครื่องบินข้ามโลกเป็นครั้งแรก นั่งดูเส้นทางการบินที่แสดงอยู่บนหน้าจอ แล้วเห็นว่าเครื่องบินมันไม่ได้บินเป็นเส้นตรงนี่นา แต่กลับบินเป็นเส้นโค้งนิดหน่อย สิ่งนี้ทำให้ผมไม่เข้าใจ เพราะด้วยความรู้เรื่องเรขาคณิตที่เรียนมาตั้งแต่ประถม วิธีการเดินทางจากจุดหนึ่งไปอีกจุดหนึ่งให้สั้นที่สุดนั้นคือการเดินทางเป็นเส้นตรง

นึกภาพว่าเราอยู่ที่มุมหนึ่งของสนามฟุตบอลแล้วต้องการเดินไปที่อีกมุมหนึ่งของสนาม การเดินผ่ากลางสนามตามแนวเส้นทแยงมุม นั่นแหละคือเส้นทางที่สั้นที่สุด ซึ่งในทางปฏิบัติเราทำแบบนั้นไม่ได้ เพราะในสนามอาจจะมีคนเตะบอลกันอยู่ หรือการเดินผ่ากลางสนามฟุตบอลบ่อย ๆ อาจจะส่งผลเสียต่อหญ้าในสนาม ดังนั้นเราจึงต้องเดินอ้อมไปตามแนวขอบสนามซึ่งไกลกว่า แต่เครื่องบินมันต้องอ้อมอะไรด้วยหรอ บินอยู่บนฟ้าก็ไม่น่ามีอะไรให้ต้องบินอ้อมนี่นา ถ้าอย่างนั้นทำไมมันไม่บินเป็นเส้นตรงเพื่อให้ได้ระยะสั้นที่สุดกันล่ะ

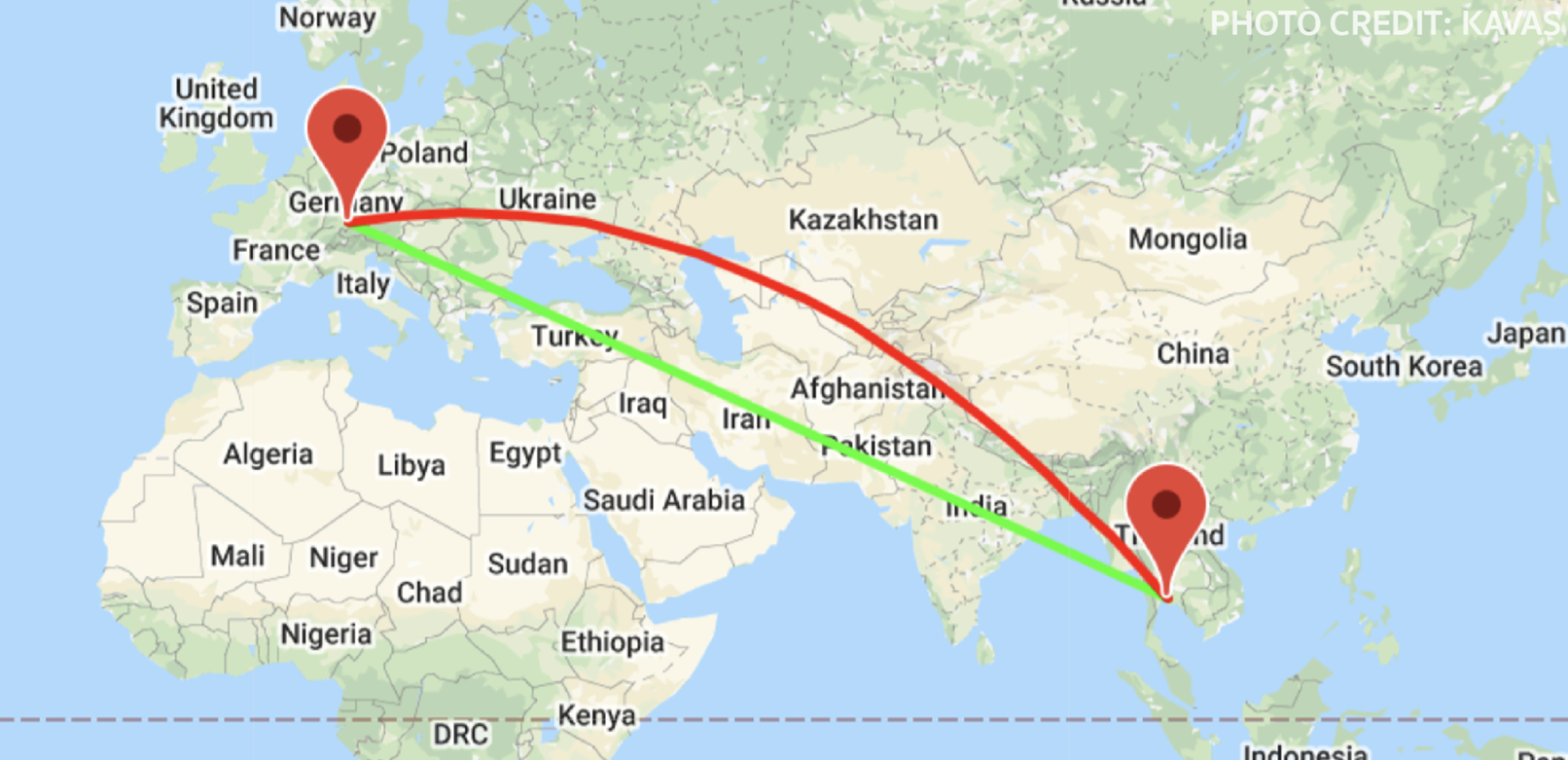
ผมเก็บคำถามนี้ไว้ในใจ จนกระทั่งได้มารู้คำตอบว่าความจริงแล้วเครื่องบินมันไม่ได้บินอ้อม มันก็บินเป็นเส้นตรงอย่างที่มันควรจะบินนั่นแหละ ถ้าเราลองคำนวณระยะทางดูจริง ๆ จะพบว่า ระยะทางตามเส้นสีเขียวนั้นเท่ากับ 9,178 กิโลเมตร ในขณะที่เส้นทางสีแดงที่ดูจะอ้อมกว่านั้นมีระยะทางเท่ากับ 8,866 กิโลเมตรเท่านั้นเอง

ข้อเท็จจริงนี้ขัดกับสามัญสำนึกของเรามากกว่าเดิม ทำไมเส้นทางสีแดงที่ดูอ้อมกว่าเห็น ๆ กลับใช้ระยะทางน้อยกว่า และเหตุผลที่อยู่เบื้องหลังข้อเท็จจริงแสนประหลาดนี้ก็คือ เพราะโลกของเรามันเป็นทรงกลม และเส้นตรงบนทรงกลมกับเส้นตรงบนแผนที่มันเป็นคนละเรื่องกัน

สิ่งที่ต้องทำความเข้าใจก็คือ แผนที่โลกที่เราใช้กันอยู่นั้นล้วนผิด เพราะโลกมันเป็นทรงกลม และเราไม่สามารถจะคลี่ทรงกลมให้มาอยู่บนแผ่นเรียบ ๆ โดยรักษาระยะทางเอาไว้ได้ ของที่อยู่ใกล้ขั้วโลกเหนือและขั้วโลกใต้จะถูกยืดออกให้ดูใหญ่เกินจริงเมื่อเทียบกับของที่อยู่ใกล้เส้นศูนย์สูตร นั่นจึงเป็นเหตุผลที่เราเห็นกรีนแลนด์หรือแคนาดาบนแผนที่โลกดูใหญ่กว่าขนาดจริงที่มันเป็น และไม่ใช่แค่ขนาดที่ผิดเพี้ยนไป แต่ทิศทางก็เหมือนกัน เส้นทางที่เราเห็นว่าสั้นที่สุดบนแผนที่ กับเส้นทางที่สั้นที่สุดจริง ๆ บนลูกโลกนั้นคือคนละเส้นกัน

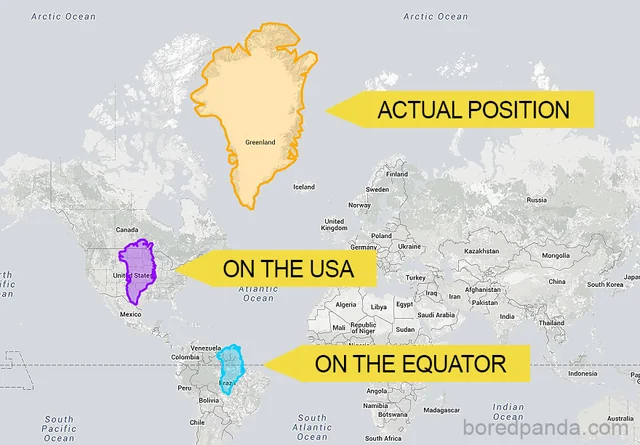
ดังนั้นคำถามต่อมาก็คือ แล้วเส้นทางที่สั้นที่สุดบนผิวโลกนั้นคือเส้นไหนกันแน่?

เพื่อที่จะตอบคำถามนี้ ลองจินตนาการว่าเรามีลูกมะนาวกลม ๆ สักลูก หยิบมีดคม ๆ สักเล่มขึ้นมา แล้วบรรจงเฉือนลงไปที่ผิวมะนาวเพื่อแบ่งมันออกเป็นสองส่วน ใครที่ยังนึกภาพไม่ออกผมอยากให้ไปลองหยิบมะนาวกับมีดมาทำตาม แล้วคุณจะพบว่ารอยตัดที่ออกมาจะเป็นรูปวงกลมเสมอ ไม่ว่าจะหั่นแนวไหนก็ตาม หรือถ้าพูดให้เป็นคณิตศาสตร์มากกว่านี้หน่อยก็คือ รอยตัดระหว่างทรงกลมกับระนาบจะออกมาเป็นวงกลมเสมอ

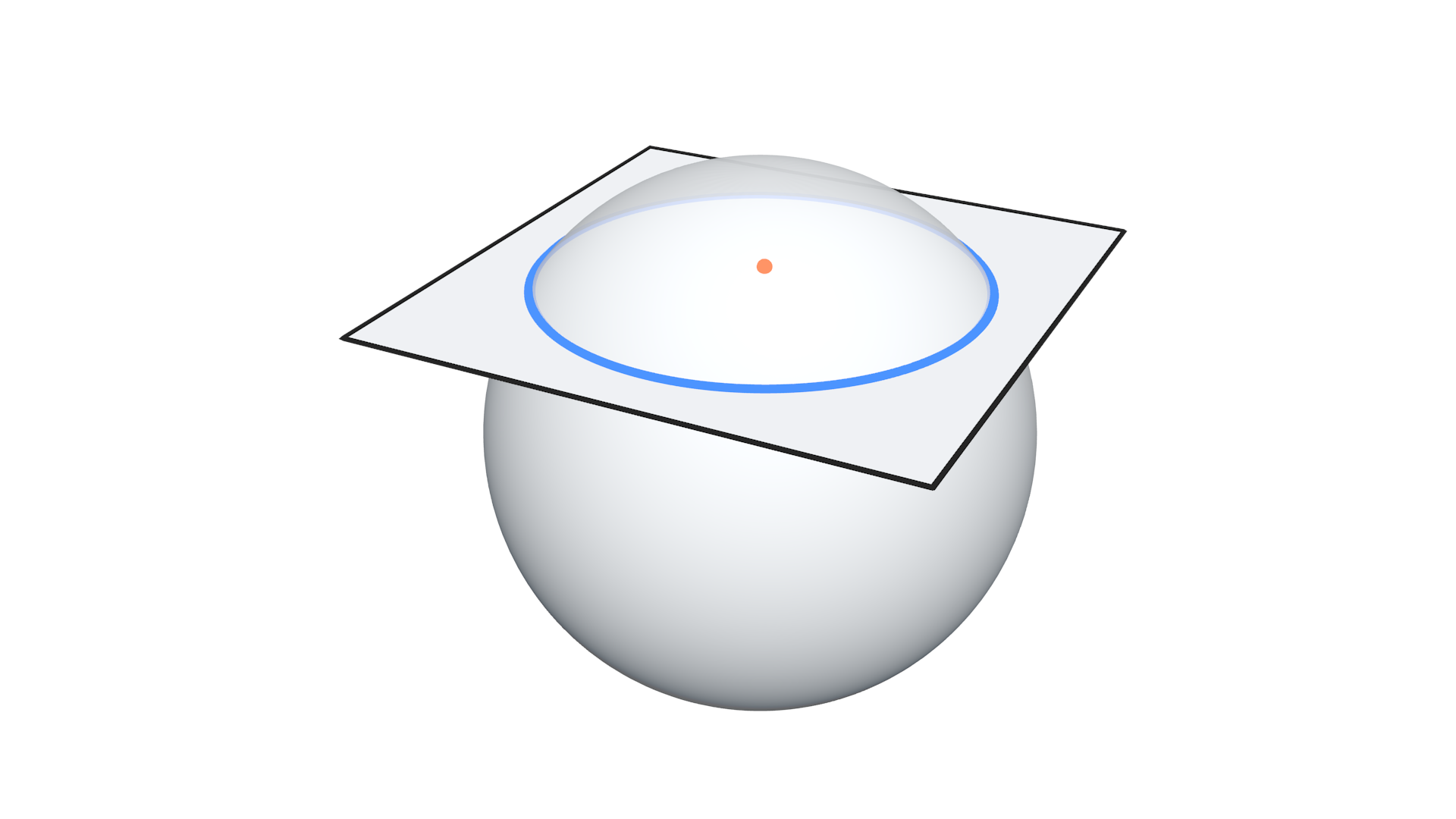
และถ้าเราลองเปลี่ยนตำแหน่งที่เฉือนมีดลงบนมะนาวดู จะพบว่าขนาดของวงกลมที่เกิดขึ้นนั้นจะต่างกันไปตามแต่ตำแหน่งและทิศทางที่ลงมีด และวงกลมที่ว่านั้นจะมีขนาดใหญ่ที่สุดเมื่อมีดของเรานั้นตัดลงไปผ่านจุดศูนย์กลางของลูกมะนาว ซึ่งเราเรียกวงกลมที่เกิดขึ้นนั้นว่า วงกลมใหญ่ (Great Circle)

กลับมาที่โลกของเรา วงกลมใหญ่ที่เรารู้จักกันดีบนโลกคือเส้นศูนย์สูตรที่ลากผ่ากลางโลกตามแนวนอน กับเส้นลองจิจูดที่ผ่ากลางโลกตามแนวตั้ง ส่วนเส้นละติจูดอื่น ๆ ที่ไม่ใช่เส้นศูนย์สูตรนั้นไม่ใช่วงกลมใหญ่ เพราะมันไม่ได้ลากผ่านศูนย์กลางของโลก

โดยเจ้าวงกลมใหญ่นี้นี่แหละ ที่รับบทเป็นเส้นทรงบนผิวทรงกลม นั่นคือถ้าเราต้องการเดินทางจากจุดหนึ่งไปอีกจุดหนึ่งบนโลก เพียงแค่เราเดินตามแนวเส้นวงกลมใหญ่ที่ผ่านสองจุดนั้น เราก็จะแน่ใจได้ว่านั่นคือเส้นทางที่สั้นที่สุด

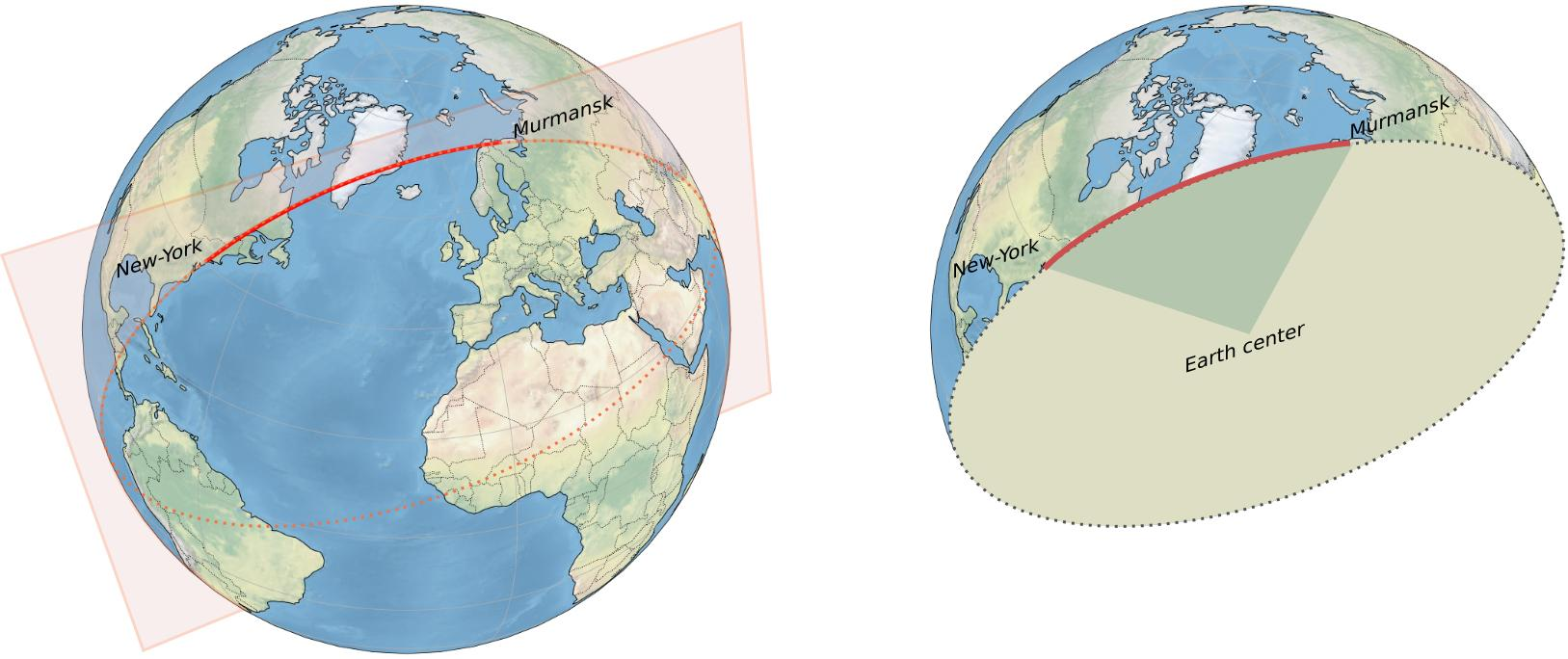
 นักคณิตศาสตร์และนักดาราศาสตร์รู้จักเส้นวงกลมใหญ่มานานแล้ว คุณคลอดิอุส ปโตเลมี (Claudius Ptolemy) ได้ใช้เส้นวงกลมใหญ่มาตั้งแต่ศตวรรษที่ 2 ในงาน Almagest ซึ่งอธิบายการเคลื่อนที่ของดาวเคราะห์ด้วยการใช้วงกลมใหญ่เป็นโมเดล ส่วนการพิสูจน์ทางคณิตศาสตร์ว่าเส้นวงกลมใหญ่เป็นเส้นทางที่สั้นที่สุดบนผิวทรงกลมนั้น ปรากฏในงานของนักคณิตศาสตร์และนักดาราศาสตร์ช่วงศตวรรษที่ 15 เช่น คุณโยฮันน์ มึลเลอร์ (Johann Müller) และคุณนิโคลัส โคเปอร์นิคัส (Nicolaus Copernicus)

ซึ่งเมื่อเป็นแบบนี้ หลายคนอาจคิดว่านักเดินเรือในยุคแห่งการสำรวจ (Age of Exploration) ซึ่งคือช่วงศตวรรษที่ 15 ถึง 17 ที่เป็นยุคที่หลายประเทศในยุโรปเริ่มออกสำรวจและเดินทางไปยังดินแดนต่าง ๆ ก็คงเดินเรือข้ามมหาสมุทรตามแนวเส้นวงกลมใหญ่ เช่นเดียวกับที่เครื่องบินในปัจจุบันทำกัน แต่ความจริงแล้วไม่เป็นอย่างนั้น นักเดินเรือในยุคนั้นไม่ได้เดินทางโดยอิงตามเส้นวงกลมใหญ่ เนื่องจากข้อจำกัดทางเทคโนโลยีที่ยังไม่เอื้อให้สามารถนำทางได้อย่างแม่นยำ สาเหตุสำคัญก็คือ การเดินทางตามเส้นวงกลมใหญ่ต้องอาศัยการระบุตำแหน่งของเรืออย่างต่อเนื่อง เพื่อให้สามารถปรับทิศทางได้ตลอดเวลา ซึ่งแม้ว่าในสมัยนั้นนักเดินเรือจะสามารถหาเส้นละติจูด ที่ตัวเองอยู่ได้อย่างแม่นยำโดยใช้ดวงอาทิตย์หรือดาวเหนือ แต่การหาเส้นลองจิจูดยังเป็นปัญหาใหญ่ นักเดินเรือยังไม่มีเครื่องมือที่ดีพอสำหรับการคำนวณลองจิจูดอย่างแม่นยำ

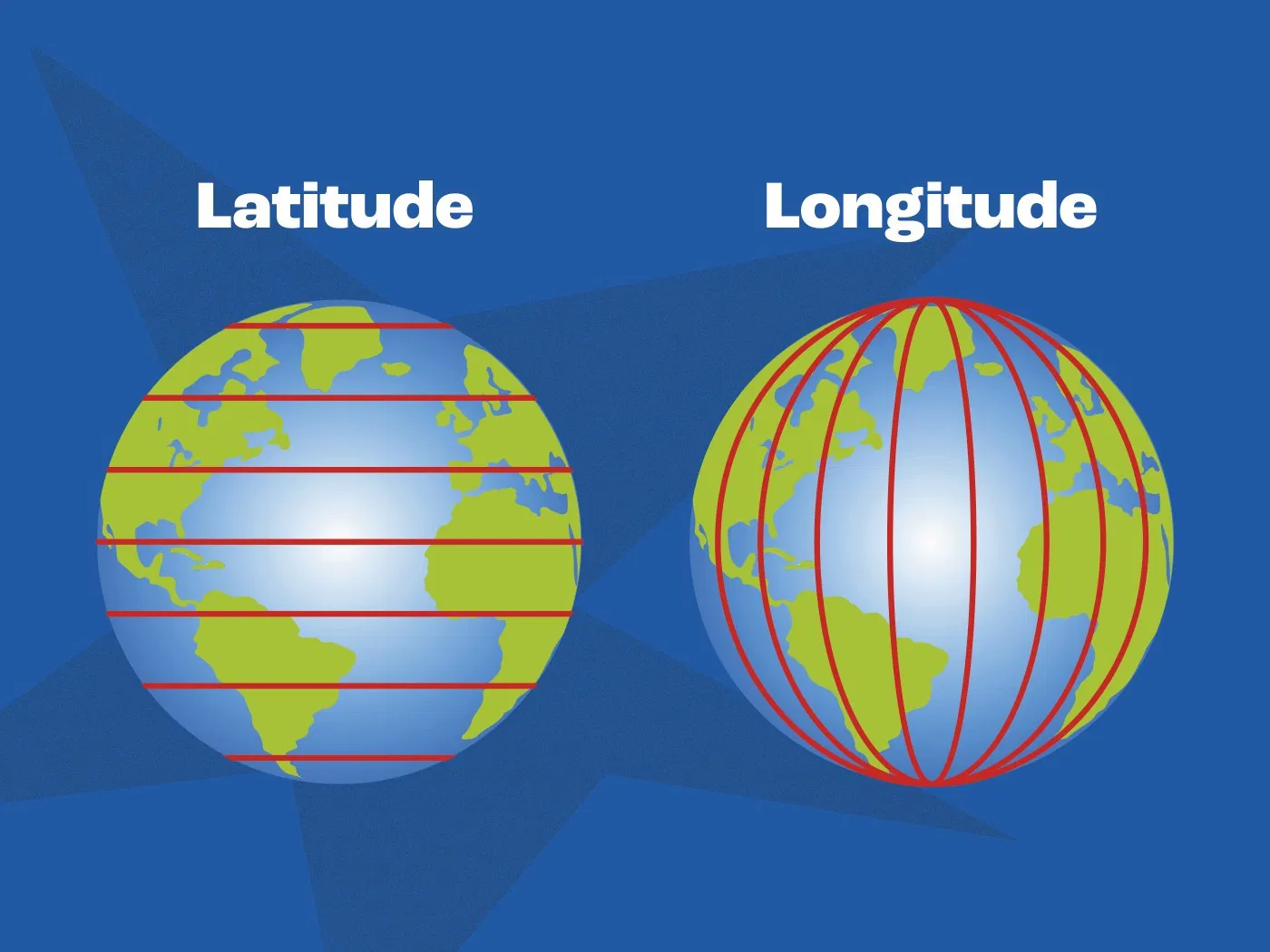
ด้วยข้อจำกัดนี้ นักเดินเรือในยุคแห่งการสำรวจจึงนิยมเดินเรือข้ามมหาสมุทรตามเส้นละติจูดคือเดินเรือขนานกับเส้นศูนย์สูตรไปเรื่อย ๆ ค่อยเปลี่ยนทิศทางเมื่อเข้าใกล้จุดหมายปลายทาง วิธีนี้ช่วยลดความผิดพลาดจากการคำนวณลองจิจูดได้ แต่ก็ทำให้ต้องเดินเรืออ้อมไปไกล

จนกระทั่งการมาถึงของคอนเซ็ปทางคณิตศาสตร์ที่เรียกว่าเส้นรัมบ์ (Rumb Line) หรือเส้นลอกซอโดรม (Loxodrome) ที่ได้ถูกศึกษาอย่างจริงจังโดยคุณเปโดร นูนส์ (Pedro Nunes) นักคณิตศาสตร์และนักดาราศาสตร์ชาวโปรตุเกสในศตวรรษที่ 16 โดยเขาได้รับมอบหมายจากราชสำนักโปรตุเกสให้ปรับปรุงวิธีการเดินเรือ เพื่อช่วยให้นักสำรวจโปรตุเกสสามารถเดินเรือได้แม่นยำขึ้น

เส้นรัมบ์คือเส้นที่ลากลงมาจากขั้วโลกเหนือ ขดลงมาเรื่อย ๆ เป็นเกลียวรอบโลกจนถึงขั้วโลกใต้ ทำมุม β กับเส้นละติจูดคงที่เสมอ

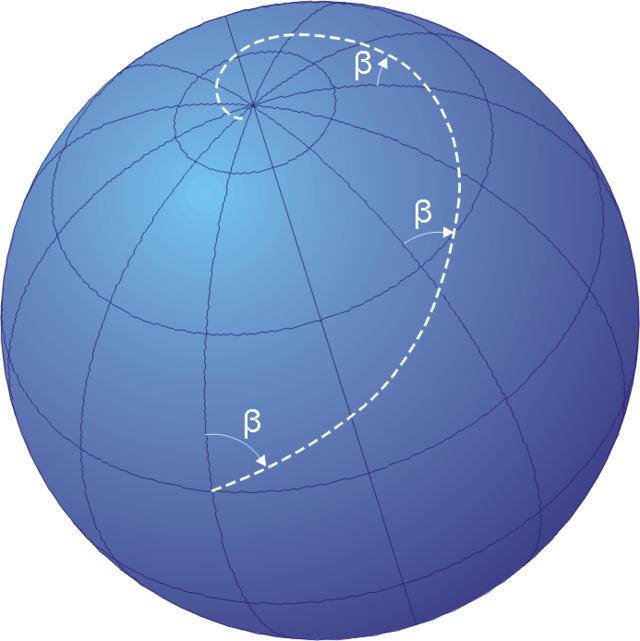
คุณเปโดร นูนส์พบว่าเส้นรัมบ์มีคุณสมบัติพิเศษ คือการรักษาทิศทางที่คงที่เมื่อวัดจากเข็มทิศ นั่นคือหากนักเดินเรือต้องการเดินเรือตามเส้นรัมบ์ พวกเขาก็แค่คำนวณมุมที่ต้องการ แล้วเดินเรือในทิศทางที่เข็มทิศชี้ไปทางเดิมเสมอ ซึ่งวิธีนี้ง่ายต่อการนำทางมากกว่าการเดินเรือตามเส้นวงกลมใหญ่ เพราะนักเดินเรือสามารถเดินทางได้โดยไม่ต้องคำนวณตำแหน่งและคอยเปลี่ยนทิศทางอยู่ตลอดเวลา

ในเชิงคณิตศาสตร์ จากมุมมองสมัยใหม่ เส้นรัมบ์เกิดจากการแก้สมการเชิงอนุพันธ์ที่อธิบายการเคลื่อนที่ในทิศทางซึ่งมุมระหว่างเส้นทางเดินเรือกับเส้นเมริเดียนคงที่ ค่ามุมนี้ให้ด้วย β เราสามารถกำหนดเส้นทางนี้เป็นสมการพาราเมตริกบนทรงกลมได้ดังนี้:

ให้ λ คือเส้นลองจิจูดและ ϕ คือเส้นละติจูด ความสัมพันธ์ระหว่าง λ และ ϕ บนเส้นโลโซโดรมเป็นดังนี้

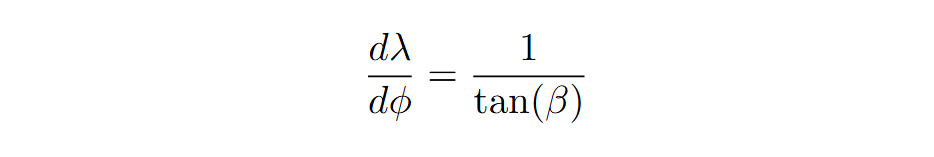
สมการนี้บอกว่าอัตราส่วนระหว่างการเปลี่ยนแปลงของเส้นแวงต่อเส้นละติจูดเป็นค่าคงที่ ซึ่งกำหนดโดยมุมคงที่ β เมื่อเรือแล่นไปตามเส้นโลโซโดรม มุมที่มันทำกับเส้นเมริเดียนจะไม่เปลี่ยนแปลงเลย

เราสามารถแปลงสมการข้างต้นให้เป็นสมการเชิงฟังก์ชันได้ดังนี้:

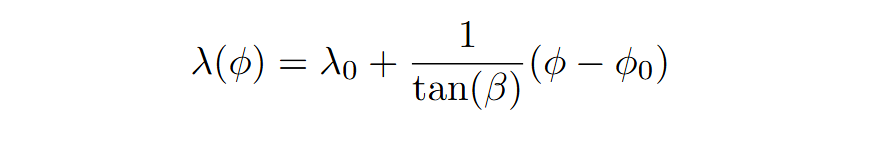
อย่างไรก็ตาม ในยุคของคุณนูเนสนั้นวิชาแคลคูลัสยังไม่ถือกำเนิดขึ้น และเขายังไม่มีเครื่องมืออย่างสมการเชิงอนุพันธ์สำหรับใช้อธิบายเส้นโลโซโดรม นูเนสจึงเข้าหาปัญหานี้ด้วยเรขาคณิต โดยอาศัยหลักการของเรขาคณิตบนทรงกลม เขาตระหนักว่าเส้นโลโซโดรมคือเส้นทางที่ตัดเส้นเมริเดียนด้วยมุมคงที่ ซึ่งเป็นแนวคิดสำคัญต่อการนำทางทางทะเล นูเนสอาจใช้วิธีเชิงประจักษ์และการสังเกตอย่างละเอียดจากการนำทางโดยดวงดาว ควบคู่กับเรขาคณิตของทรงกลมและความจำเป็นที่จะต้องรักษาทิศเข็มทิศให้คงที่ มากกว่าการใช้เครื่องมือทางคณิตศาสตร์แบบเป็นทางการที่เราใช้กันในปัจจุบัน

และแม้ว่าการเดินทางตามเส้นรัมบ์จะใช้ระยะทางมากกว่าเส้นวงกลมใหญ่ แต่มันช่วยให้นักเดินเรือสามารถใช้เครื่องมือที่มีอยู่ในยุคนั้น เช่น เข็มทิศ และแผนที่แบบเมอร์เคเตอร์ (Mercator Projection) ที่พัฒนาโดยคุณเคราร์ดุส เมอร์เคเตอร์ (Gerardus Mercator) ในศตวรรษที่ 16 ซึ่งแสดงเส้นรัมไลน์เป็นเส้นตรง ทำให้นักเดินเรือสามารถใช้เส้นทางนี้ได้ง่ายกว่าการคำนวณเส้นวงกลมใหญ่

หากใครมีโอกาสได้แวะไปเที่ยวลิสบอน เมืองหลวงของประเทศโปรตุเกส ก็จะพบกับอนุสาวรีย์ของเปโดร นูนส์ ที่สร้างขึ้นเพื่อเป็นเกียรติแก่คุณูปการณ์ที่เขาค้นพบเส้นรัมไลน์ ซึ่งมีประโยชน์อย่างมากในยุคสำรวจ เพราะช่วยให้การเดินเรือในมหาสมุทรทำได้ง่ายขึ้น มีรูปปั้นของเขาเป็นหนึ่งใน 33 รูปปั้นบุคคลสำคัญที่อนุสาวรีย์แห่งการค้นพบ (Monument to the Discoveries) ริมแม่น้ำทากัส ในย่านเบเล็ม โดยถ้าเรายืนมองอนุสาวรีย์แห่งนี้ทางฝั่งตะวันออก นูเนสจะยืนอยู่ลำดับที่ 5 สังเกตง่าย ๆ ว่าเป็นผู้ชายที่ถือลูกโลกอยู่ในมือ

หรือที่ปลายด้านใต้ของสวนคัมโป กรานเด (Campo Grande) จะมีงานศิลปะหน้าตาเป็นลูกกลม ๆ ที่มีลากเส้นเป็นแถบ ๆ สำหรับคนทั่วไป นี่อาจจะดูเหมือนก็เป็นแค่งานศิลปะสักชิ้นหนึ่งเท่านั้น เพราะมันไม่ได้มีคำอธิบายหรือป้ายอะไรบอกอยู่เลย แต่สำหรับคนที่รู้ จริง ๆ แล้วทรงกลมที่เห็นนั้นคือลูกโลก และเส้นที่เห็นว่าลากเป็นเกลียวรอบ ๆ มันนั้นคือเส้นรัมบ์นั่นเอง

การเดินทางตามเส้นวงกลมใหญ่สั้นที่สุดนั้นเพิ่งเริ่มได้รับความนิยมอย่างแท้จริงในช่วงปลายศตวรรษที่ 19 และต้นศตวรรษที่ 20 นี้เอง จากการพัฒนาเครื่องมือระบุตำแหน่งที่แม่นยำขึ้น เช่น นาฬิกาทะเล (Marine Chronometer) ระบบนำทางแบบเรดิโอ (Radio Navigation) และในยุคปัจจุบัน ระบบ GPS ซึ่งทำให้สามารถคำนวณและติดตามเส้นทางที่สั้นที่สุดได้อย่างแม่นยำ

เรื่องราวของเรขาคณิตบนผิวทรงกลมและการเดินทางนี้แสดงให้เห็นว่า คณิตศาสตร์ที่แม้จะดูเป็นเรื่องนามธรรมและไกลตัว แท้จริงแล้วอยู่ใกล้ตัวและสำคัญกับเรามากกว่าที่คิด มนุษยชาติศึกษาคณิตศาสตร์เพื่อทำความเข้าใจและแก้ปัญหา การเรียนคณิตศาสตร์จึงไม่ใช่แค่เรื่องของทฤษฎี แต่มันยังเป็นเครื่องมือสำคัญที่ช่วยขับเคลื่อนการค้นคว้าและนวัตกรรม เพื่อพัฒนาให้สิ่งต่าง ๆ ดีขึ้น

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง
https://www.cim.pt/magazines/bulletin/3/article/31/pdf
http://cvc.instituto-camoes.pt/ciencia_eng/e42.html
https://getlisbon.com/discovering/mathematics-campo-grande-garden/
https://www.atractor.pt/mat/loxodromica/saber_parametrizacao1-_en.html
https://link.springer.com/chapter/10.1007/978-3-642-04833-3_16