เซตคืออะไร

เซตคืออะไร เป็นคำถามโลกแตกที่ผมเลี่ยงจะตอบเสมอเวลาถูกถาม ไม่ใช่เพราะว่าไม่รู้ แต่เพราะว่ามันยาว เข้าใจยาก และมีรายละเอียดเยอะ กลัวพูดแล้วผิด แต่วันนี้ไม่รู้นึกครึ้มอะไร จะลองดูสักตั้งแล้วกันฮะ

แต่ก่อนจะไปคุยกันว่าเซตคืออะไร เอาให้ชัดก่อนว่าเซตนั้นไม่ใช่ 'กลุ่มของอะไรสักอย่าง' ตามที่คนชอบพูดกัน แม้ในบางโอกาสผมเองก็พูด เพราะนั่นมันคือวิธีการอธิบายความหมายเซตที่เห็นภาพได้ง่ายที่สุด เซตของสระในภาษาอังกฤษก็คือ {a, e, i, o, u} เซตของจำนวนเต็มบวกคู่ก็คือ {2, 4, 6, ...} แต่นั่นไม่ใช่ความหมายที่ถูกต้องของคำว่าเซต

เซตจะหมายถึงกลุ่มของอะไรก็ได้ไม่ได้ เพราะถ้าเซตหมายถึงกลุ่มของอะไรก็ได้จริง งั้นถ้าเรานิยามให้ R เป็นเซตของบรรดาเซตทั้งหมดที่ไม่ได้เป็นสมาชิกของตัวเอง

คำถามคือ แล้ว R เป็นสมาชิกของตัวมันเองรึเปล่า

ถ้า R เป็นสมาชิกของตัวเอง แปลว่ามันไม่ควรเป็นสมาชิกของตัวเอง และถ้ามันไม่เป็นสมาชิกของตัวเอง แปลว่ามันควรเป็นสมาชิกของตัวเอง ข้อขัดแย้งนี้ถูกยกขึ้นมาโดยคุณ Bertrand Russell ซึ่งทำให้นักคณิตศาสตร์ในยุคนั้นได้รู้ว่าความเข้าใจเกี่ยวกับเซตในอดีตนั้นยังมีปัญหาและต้องได้รับการแก้ไขให้รัดกุมขึ้น เซตไม่ใช่แค่กลุ่มของอะไรก็ได้ แต่มันต้องการเงื่อนไขบางอย่าง ที่ทำให้เซตเป็นเซต

ยัง ผมยังเข้าเรื่องไม่ได้ คุณยังไม่พร้อมรู้ว่าเซตคืออะไร มีอีกอย่างที่คุณต้องรู้จักก่อน นั่นคือคำว่า Axiom หรือภาษาไทยว่าสัจพจน์ ซึ่งถ้าคุณได้อ่านบทความชุด Why Abstraction? คุณน่าจะเคยได้ยินคำนี้มาแล้ว

สำหรับคนที่ไม่ได้อ่าน สัจพจน์คือข้อความที่ถือกันว่าจริงโดยไม่ต้องพิสูจน์ ซึ่งนักคณิตศาสตร์ไม่ชอบ เพราะนักคณิตศาสตร์ชอบอะไรที่พิสูจน์ได้ ดังนั้นการมีสัจพจน์เยอะ ๆ จึงแปลว่ามีของที่เราต้องเชื่อว่าจริงโดยไม่พิสูจน์อยู่เยอะ ดังนั้นนักคณิตศาสตร์จะพยายามสร้างระบบให้มีสัจพจน์น้อยข้อที่สุด และแต่ละข้อนั้นควรจะสั้น กระชับ และเห็นว่าควรเป็นจริงโดยไม่เกิดการถกเถียง ไม่อย่างนั้นสัจพจน์ก็จะไม่เป็นสัจพจน์ถูกไหมฮะ

เซตถูกนิยามด้วยสัจพจน์หลายข้อ ซึ่งเวอร์ชันที่ใช้กันอย่างแพร่หลายที่สุดนั้นเรียกกันว่า สัจพจน์ของ Zermelo–Fraenkel ตามชื่อของนักคณิตศาสตร์สองคนที่ออกแบบระบบนี้ขึ้นมาในช่วงปี 19 นิด ๆ โดยพวกเขาไม่ได้บอกตรง ๆ ว่า 'เซตคืออะไร' แต่บอกว่า 'อะไรบ้างคือเซต'

โดยข้อแรกสุดบอกว่า

มีเซตที่ไม่มีสมาชิกอยู่เลย

และข้อสองบอกว่า

เซตสองเซตจะเท่ากัน เมื่อมันมีสมาชิกเหมือนกันทุกตัว

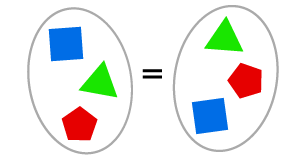
ซึ่งเมื่อเราสมมติว่าสองข้อนี้จริง เราจะได้ว่า 'เซตที่ไม่มีสมาชิกอยู่เลย' นั้นมีเซตเดียว เพราะหากเราหยิบเซตที่ไม่มีสมาชิกอยู่เลยมาสองอัน มันจะต้องเท่ากันตามสัจพจน์ข้อสอง ดังนั้นพอมั่นใจว่ามันมีอันเดียว เราก็ตั้งชื่อและกำหนดสัญลักษณ์ให้มันได้ เรียกมันว่าเซตว่าง และใช้สัญลักษณ์คือ ∅

ถึงตรงนี้เราเพิ่งมีเซตแค่เซตเดียวเองคือเซตว่าง และเพื่อให้เราสามารถสร้างเซตชนิดอื่น ๆ ได้นั้น เราต้องการ สัจพจน์การจับคู่ ที่บอกว่า

ถ้า A และ B เป็นเซต เราจะได้ว่า {A, B} นั้นก็เป็นเซตด้วย

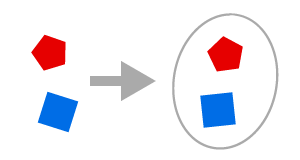
ตอนนี้เรารู้แล้วนี่นาว่า ∅ เป็นเซต ดังนั้นโดยสัจพจน์การจับคู่เราจะได้ว่า {∅, ∅} นั้นก็เป็นเซต แต่ด้วยความที่ ∅ นั้นมีตัวเดียว ดังนั้นจึงเขียนแค่ {∅} ก็พอ

คราวนี้เราก็สนุกใหญ่เลยสิฮะ เพราะโดยสัจพจน์การจับคู่เราจะได้ว่า {∅, {∅}} นั้นเป็นเซต {∅, {{∅}}} ก็เป็นเซต โห เหมือนจะสร้างเซตได้เยอะแยะไปหมดเลย แต่ถ้าดูดี ๆ เราจะเห็นว่า โดยสัจพจน์การจับคู่เราสร้างได้แค่เซตที่มีสมาชิก 2 ตัวเท่านั้น แม้แต่เซตง่าย ๆ อย่าง {∅, {∅}, {{∅}}} เรายังสร้างไม่ได้เลย จึงเป็นที่มาของสัจพจน์ข้อถัดมาที่ชื่อว่า สัจพจน์การรวม ที่บอกว่า

การเอาสมาชิกจาก 'หลาย ๆ' เซตมารวมกันนั้นยังเป็นเซต

เช่นจากเดิมที่เรารู้ว่า {∅, {∅}} และ {{{∅}}} นั้นเป็นเซต เราก็สามารถเอาสมาชิกของทั้งสองเซตมารวมกันกลายเป็นเซตใหม่คือ {∅, {∅}, {{∅}}} ซึ่งมีสมาชิกสามตัวได้

คราวนี้สนุกกว่าเดิมอีก เพราะจะเอาเซตกี่เซตมารวมกัน สร้างเป็นเซตที่มีสมาชิกกี่ตัวก็ได้

ซึ่งอ่านมาถึงตรงนี้ ถ้าคุณคิดตามดี ๆ คุณจะเริ่มเอะใจว่า ถ้าสัจพจน์การรวมทำให้เราสร้างเซตที่มีสมาชิกที่มีขนาดกี่ตัวก็ได้อยู่แล้ว งั้นทำไมเราถึงยังต้องการสัจพจน์การจับคู่ที่สร้างได้แค่เซตขนาดสองตัวอยู่อีกล่ะ ไหนว่านักคณิตศาสตร์ไม่ชอบให้มีสัจพจน์เยอะ ๆ ไง แล้วจะใส่สัจพจน์การจับคู่ที่เหมือนเป็นแค่กรณีเฉพาะของสัจพจน์การรวมมาด้วยทำไม

คำตอบก็คือ เพราะถ้าเราข้ามสัจพจน์การจับคู่ แล้วเอาสัจพจน์การรวมมาเป็นสัจพจน์ข้อสาม เราจะสร้างเซตอะไรเพิ่มจากเซตว่างไม่ได้เลย เพราะถ้าลองย้อนกลับไปอ่านดี ๆ จะเห็นว่าการจะใช้สัจพจน์การรวมได้นั้น เราต้องมีเซตที่มีสมาชิกอยู่ข้างในอยู่ก่อน ซึ่งเซตว่างไม่มีสมาชิก ดังนั้นเราจึงต้องใช้สัจพจน์การจับคู่เพื่อสร้างเซตที่สมาชิกอยู่ข้างในขึ้นมาก่อน แล้วค่อยใช้สัจพจน์การรวมมาสร้างเซตที่มีขนาดใหญ่ขึ้นต่อไป

มาถึงตรงนี้เหมือนว่าเราจะสร้างเซตที่มีขนาดเท่าไรก็ได้ตามใจเราหมดแล้ว เพราะอยากสร้างเซตที่มีขนาดเท่าไร ก็แค่ค่อย ๆ ขยายขนาดมันขึ้นไปด้วยสัจพจน์การรวม แต่ไม่ใช่ฮะ เรายังสร้างเซตขนาดนึงไม่ได้ นั่นคือเซตที่มีขนาดเป็นอนันต์

ในโลกความเป็นจริงเรารู้จักกับเซตอนันต์เยอะมาก อย่างเซตของจำนวนนับหรือจำนวนเต็ม ซึ่งด้วยสัจพจน์ทั้งสี่ข้อที่เรามีอยู่ตอนนี้ เรายังไม่สามารถพูดว่าเซตอนันต์นั้นมีจริงได้ ดังนั้นเราจึงต้องการสัจพจน์ข้อถัดมาที่บอกว่า

{∅, {∅}, {∅,{∅}}, {∅,{∅},{∅,{∅}}}, …} นั้นเป็นเซต

ใจเย็น ๆ คุณอย่าเพิ่งตื่นกลัว ค่อย ๆ ดูสมาชิกแต่ละตัว เริ่มต้นจากตัวแรกคือ ∅ ส่วนตัวที่สองซึ่งคือ {∅} นั้นมองได้ว่าเป็นการเอา ∅ มารวมกับ {∅} ส่วนตัวที่สามซึ่งคือ {∅, {∅}} นั้นมันคือการเอา {∅} มารวมกับ {{∅}} หรือพูดเป็นกรณีทั่วไปคือ ถ้าตัวก่อนหน้าคือ X ตัวถัดไปจะเป็น X รวมกับ {X} แบบนี้ไปเรื่อย ๆ นั่นเอง

สัจพจน์ข้อนี้ถูกเรียกว่า สัจพจน์อนันต์ เพราะมันคือสัจพจน์ที่ทำให้เรารู้จักเซตอนันต์เป็นครั้งแรก ซึ่งต่อมาเซตอนันต์แรกที่เรารู้จักนี้จะถูกเรียกว่าเซตของจำนวนนับ โดยมองว่า

∅ คือเลข 0
{∅} คือเลข 1
{∅,{∅}} คือเลข 2
{∅,{∅},{∅,{∅}}} คือเลข 3
และไปเรื่อย ๆ

นั่นจึงเป็นเหตุผลที่นักคณิตศาสตร์บางคน โดยเฉพาะที่ใกล้ชิดกับวิชาทฤษฎีเซต ถึงนิยมนับว่าศูนย์เป็นจำนวนนับตัวแรก แทนที่จะเป็นหนึ่งอย่างที่เราคุ้นเคย

ความจริงแล้วสัจพจน์ของ Zermelo–Fraenkel ไม่ได้หมดแค่นี้นะฮะ มันยังมีอีก แม้ว่าด้วยห้าข้อนี้ที่เรามีมันถึงมันจะสร้างเซตอนันต์อย่างจำนวนนับได้แล้ว แต่มันยังสร้างเซตอนันต์ที่ใหญ่กว่านั้นอย่างเซตของจำนวนจริงไม่ได้เลย จึงต้องมีสัจพจน์ข้ออื่น ๆ ตามมาอีกนิดหน่อย ซึ่งผมจะขออนุญาตหยุดตรงนี้แล้วทิ้งไว้ให้ไปหาอ่านกันต่อ

เราเรียกกลุ่มของอะไรสักอย่างที่ไม่เป็นเซตว่า proper class ซึ่งอันที่โด่งดังก็เช่น กลุ่มของเซตทั้งหมด กลุ่มของ group ทั้งหมด หรือกลุ่มของ vector space ทั้งหมด

แน่นอนว่าในทางปฏิบัติ เวลาพูดว่าเซตผมก็จะนึกภาพถึง 'กลุ่มของอะไรสักอย่าง' อยู่ดีนั่นแหละ เพราะเซตที่คนทั่ว ๆ ไปมีเหตุให้ต้องข้องเกี่ยวด้วยนั้นไม่ได้อยู่ในจุดที่สุ่มเสี่ยงจะไม่เป็นสักหน่อยนี่นา

แต่เหตุผลที่ผมหยิบเรื่องนี้มาเล่าให้ฟังก็เพื่อให้ทุกคนได้เห็นว่า จริง ๆ แล้วสิ่งที่เราคิดว่าง่าย ๆ และเหมือนจะตรงไปตรงมาอย่าเซต พอเราตั้งใจมองและศึกษาให้ลึกลงไป กลับพบว่ามันซับซ้อนและมีอะไรให้ต้องละเอียดกว่าที่คิดเยอะ

และถ้าหลังจากนี้ ทุกครั้งที่คุณพูดว่าเซตคือกลุ่มของอะไรสักอย่าง แล้วแอบกระซิบกับตัวเองในใจว่า จริง ๆ แล้วมันไม่ใช่กลุ่มของอะไรก็ได้นะ แค่นี้ผมก็ถือว่าบทความนี้ของผมประสบความสำเร็จแล้วครับ

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

เอกสารอ้างอิง
https://www.chulabook.com/test-prep/20349
https://plato.stanford.edu/entries/set-theory/index.html
https://people.math.ethz.ch/~halorenz/4students/LogikGT/Ch13.pdf
https://link.springer.com/chapter/10.1007/978-3-030-52279-7_13