ทำไมเพื่อนของเราถึงมีเพื่อนเยอะกว่าเราตลอดเลย

เคยรู้สึกกันไหมว่าทำไมเพื่อนของเราส่วนใหญ่ถึงดูเหมือนว่าจะมีเพื่อนเยอะกว่าเราเสมอเลย เวลาเดินไปไหนมาไหน ก็จะเห็นว่าเพื่อนเรามันทักคนนั้นคนนี้ที่เราไม่รู้จัก หรือในวงสนทนาเดี๋ยวมันก็พูดถึงเพื่อนที่อื่นที่เราไม่รู้จักขึ้นมาอีกแล้ว อย่างกับเพื่อนเราทุกคนดูเหมือนจะมีเพื่อนที่ไหนก็ไม่รู้อีกเยอะแยะไปหมดเลย ในขณะที่เรามีเพื่อนแค่นิดเดียวเอง

คำอธิบายที่ฟังดูเป็นวิชาการหน่อยเกี่ยวกับปรากฎการณ์นี้คือเรื่องของ Sampling Bias หรือการสุ่มตัวอย่างที่มีอคติ คืออธิบายว่าจริง ๆ ในโลกนี้มันก็มีเพื่อนที่ทั้งเพื่อนเยอะและน้อยกว่าเรานั่นแหละ แต่เราไม่ค่อยได้โฟกัสไปที่เพื่อนที่ไม่ค่อยมีเพื่อนไง เพราะว่าคนพวกนั้นมันก็ไม่ค่อยจะมาเป็นเพื่อนเราด้วยแหละ พอเรามัวแต่โฟกัสแต่คนที่เพื่อนเยอะ ๆ เราก็เลยเผลอคิดไปเองว่าเพื่อนส่วนใหญ่มีเพื่อนมากกว่าเรานั่นเอง

ครับ แม้คำอธิบายนี้จะฟังดูเข้าท่าและดูเหมือนเราคิดไปเอง แต่ความจริงไม่ใช่เช่นนั้น เราไม่ได้คิดไปเอง โดยส่วนใหญ่แล้วเพื่อนของเรามีเพื่อนมากกว่าเราจริง ๆ

เราเรียกปรากฏการณ์นี้ว่า Friendship Paradox ครับ ที่มันถูกเรียกว่า Paradox ก็เพราะมันช่างฟังดูขัดกับสามัญสำนึกเหลือเกิน ลองนึกภาพว่าในโลกนี้มันก็ต้องมีคนที่เพื่อนเยอะและเพื่อนน้อยกว่าเรากระจายกันไปถูกไหมฮะ แล้วโดยส่วนใหญ่แล้วเพื่อนของทุกคนจะมีเพื่อนมากกว่าเจ้าตัวเสมอได้ยังไง

เจ้า Paradox นี้ถูกพูดถึงครั้งแรกโดย Scott L. Feld นักสังคมวิทยาท่านหนึ่งในบทความเรื่อง Why Your Friends Have More Friends Than You Do เมื่อปี 1991 เค้าค้นพบว่า สมมุติว่าคุณมีเพื่อนอยู่ 50 คน แล้วเพื่อนทั้ง 50 คนของคุณนั้นเค้าก็มีจำนวนเพื่อนของตัวเองเนอะ เอาจำนวนเพื่อนของเพื่อนเขาทั้ง 50 คนนั้นมาเฉลี่ยกัน โดยส่วนใหญ่แล้วเลขที่ได้ออกมาจะมีค่ามากกว่า 50 เสมอ หรือที่แปลว่า “โดยเฉลี่ยแล้วเพื่อนของเราจะมีเพื่อนมากกว่าเรา” นั่นเอง

Paradox อันนี้นั้นสามารถพิสูจน์ให้เห็นได้ว่าจริงด้วยแขนงหนึ่งในคณิตศาสตร์ที่เรียกว่าทฤษฎีกราฟ โดยจำลองคนแต่ละคนเป็นจุดยอด และจำลองความสัมพันธ์ของคนผ่านการโยงเส้นเชื่อม อย่างเช่นตัวอย่างในรูปด้านล่าง จะเห็นว่าเราสนใจคน 4 คน คือ A,B,C และ D ซึ่งคนคู่ไหนที่มีเส้นเชื่อมกัน ก็แปลว่าเขาเป็นเพื่อนกัน

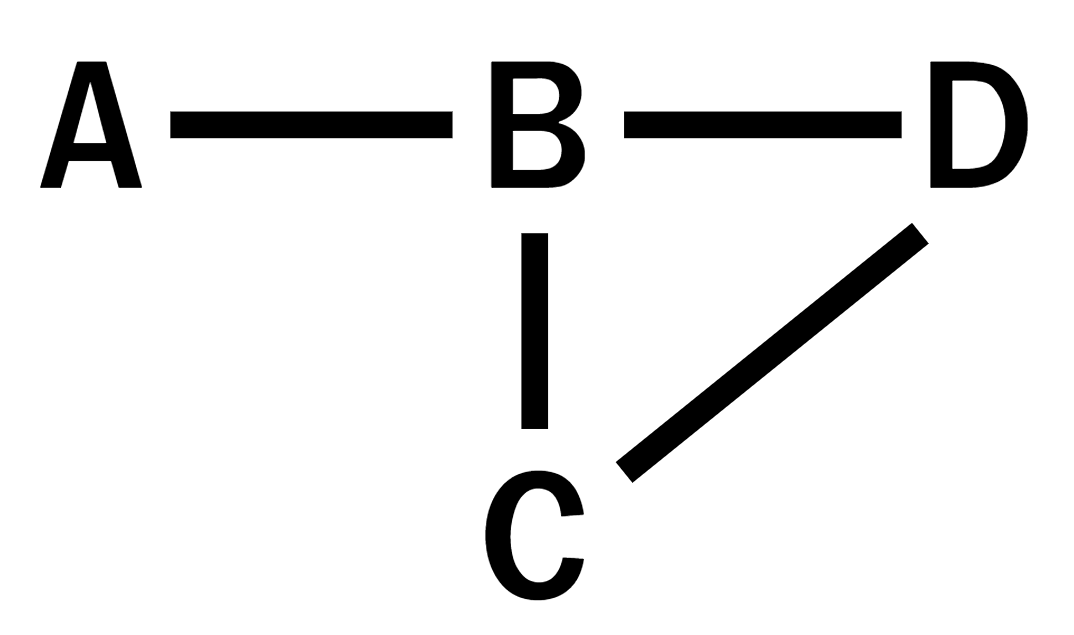
แน่นอนว่าแบบจำลองนี้ก็ไม่ได้สามารถใช้อธิบายความสัมพันธ์ในความเป็นจริงได้ดีนัก เพราะในความจริงคือเราอาจจะต้องแยกอีกว่าที่ว่าเป็นเพื่อนนั้นคือเพื่อนสนิท เพื่อน หรือแค่คนรู้จักเฉย ๆ หรืออาจจะมีกรณีเศร้า ๆ อย่างคิดไปเองว่าเป็นเพื่อนใครฝ่ายเดียว แต่ถ้าเราลองคิดถึงกรณีง่าย ๆ อย่างการเป็นเพื่อนกันใน Facebook แบบจำลองนี้ก็น่าจะใช้ได้ดีทีเดียว

กลับมาที่กลุ่มเพื่อน A, B, C และ D เมื่อสักครู่นี้

ลองเริ่มคำนวณจากของ A ดูก่อน จากกราฟจะเห็นว่า A นั้นมีเพื่อน 1 คน ซึ่งคือ B แต่ด้วยความที่ B มีเพื่อน 3 คน ดังนั้นจำนวนเพื่อนเฉลี่ยของเพื่อน A จึงเท่า 3 คน นั่นเอง

ลองคิดของ B ดูบ้าง เขามีเพื่อน 3 คน คือ A C และ D ซึ่งแต่ละคนมีเพื่อนเท่ากับ 1 2 และ 2 ตามลำดับ เฉลี่ยออกมาได้ 1.67 ซึ่งคือจำนวนเพื่อนเฉลี่ยของเพื่อน B นั่นเอง

คุณลองคำนวณของ C และ D ดูเอง แต่ผมแอบสปอยด์ว่าได้ 2.5 ดังนั้นจึงได้ตารางออกมาดังนี้

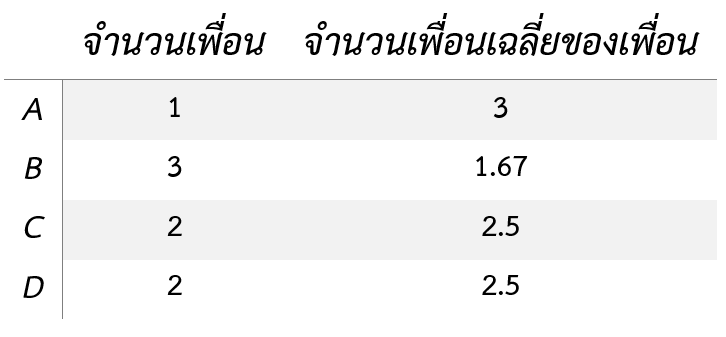
ซึ่งสิ่งที่คุณจะเห็นได้ก็คือ มีแค่ B เท่านั้น ที่มีจำนวนเพื่อนมากกว่าจำนวนเพื่อนเฉลี่ยของเพื่อนของตัวเอง ส่วน A C และ D นั้นมีเพื่อนน้อยกว่าจำนวนเพื่อนเฉลี่ยของเพื่อนของตัวเองหมดเลย ตรงกับที่ Friendship Paradox บอกว่าเป๊ะ ๆ

เราสามารถพิสูจน์ได้ว่า Friendship Paradox นั้นจริงในกรณีทั่ว ๆ ไป หมายความว่าในกราฟความสัมพันธ์ของคนกลุ่มไหนก็ตาม นั่นคือคนส่วนใหญ่ในกลุ่มจะมีเพื่อนน้อยกว่าจำนวนเพื่อนเฉลี่ยของเพื่อนของตัวเองกันทั้งนั้น โดยบทพิสูจน์ต้องใช้พื้นฐานทฤษฏีกราฟ แล้วก็ความอดทนทำความเข้าใจนิดหน่อย เดี๋ยวผมจะแปะเอาไว้ให้ท้ายบทความ

หนึ่งหลักฐานเชิงประจักษ์ที่มาสนับสนุนเจ้า Friendship Paradox นี้คือผลสำรวจโดยสถาบันวิจัยพิวหรือ Pew Research Center เมื่อปี 2011 ซึ่งพบว่าโดยเฉลี่ยแล้วคนใน Facebook จะมีเพื่อนใน friend list อยู่ 245 คน แต่จำนวนเพื่อนเฉลี่ยของเพื่อนแต่ละคนนั้นอยู่ที่ 359 คน ซึ่งก็สอดคล้องกับ Friendship Paradox เป็นอย่างดี

เพราะฉะนั้นใครที่กำลังรู้สึกสงสัยว่าเรานั้นไม่ค่อยฮอตรึเปล่า ทำไมไม่เห็นมีเพื่อนเยอะเหมือนเพื่อน ๆ ของเราเลย ก็จงรู้ไว้ว่า คุณอาจจะไม่ได้รู้สึกไปเอง มันอาจจะเป็นอย่างนั้นจริง ๆ แต่ก็ไม่ต้องน้อยใจไป คนส่วนใหญ่ก็เป็นแบบนั้นกันทั้งนั้นแหละ

Friendship Paradox ถูกเอาไปประยุกต์ใช้ในหลากหลายวงการ ตั้งแต่การวิเคราะห์สังคมออนไลน์เพื่อทำการตลาด การสุ่มตัวอย่างเพื่อทำแบบสำรวจ ไปจนถึงการยับยั้งการแพร่กระจายของโรคระบาดอีกด้วย

ในคณิตศาสตร์มี Paradox ที่หมายถึงข้อเท็จจริงที่ขัดกับความรู้สึกของเราแบบนี้อยู่อีกมากมาย และ Paradox เหล่านี้ก็คอยเตือนพวกเราว่าว่า บางครั้งสามัญสำนึกของคนเราก็อาจจะไม่ได้ถูกต้องเสมอไป การพิสูจน์ทางคณิตศาสตร์ที่รัดกุมเท่านั้นที่จะบอกได้ว่าอะไรจริงหรือไม่จริงกันแน่

และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ

แหล่งอ้างอิง
https://qubeshub.org/resources/740/download/ModuleFPQ.pdf
https://mindyourdecisions.com/blog/2012/09/04/why-your-friends-have-more-friends-than-you-the-friendship-paradox/
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0012948
https://arxiv.org/html/2412.02061v1
https://kdd.org/kdd2023/wp-content/uploads/2023/11/yang2023friendship.pdf