เกม XO นั้นน่าเบื่อมาก ถึงจะเพิ่มเป็น 3 มิติแล้วก็เถอะ

ตอนเด็ก ๆ ผมว่าทุกคนน่าจะเคยเล่นเกม XO หรือ Tic-Tac-Toe กันมาทั้งนั้นแหละ กติกาก็ง่ายมาก วาดกระดาน 3×3 ขึ้นมา แล้วก็แค่ผลัดกันเขียน X กับ O ลงในช่อง แล้วพยายามเรียงให้ได้สามตัวติดกันในแนวตรง แนวนอน หรือแนวทแยง ซึ่งถ้าใครเคยเล่นบ่อย ๆ ก็จะรู้ว่า ส่วนใหญ่แล้วเกมมักจะจบด้วยการเสมอ
สิ่งนี้ไม่ได้เป็นแค่ความรู้สึกส่วนตัวเท่านั้น แต่สามารถพิสูจน์ทางคณิตศาสตร์ได้ด้วยว่า ถ้าทั้งสองคนเล่นอย่างไม่พลาดเลย หรือที่เรียกว่าเล่นแบบ perfect play เกม XO แบบ 3×3 นั้นจะจบด้วยการเสมอเสมอ จะมีฝ่ายใดฝ่ายหนึ่งชนะได้เมื่ออีกฝ่ายเล่นพลาดเท่านั้น
นั่นจึงทำให้เกม XO ก็จะกลายเป็นเกมน่าเบื่อเมื่อเล่นไปสักพัก เพราะถ้าเล่นเก่งกันทั้งคู่ เล่นไปยังไงก็ไม่มีใครชนะ
แล้วถ้าเราลองขยับขึ้นไปในสามมิติบ้างล่ะ คือแทนที่จะวาง X กับ O ในตาราง 3×3 ธรรมดา เราเปลี่ยนมาวางในลูกบาศก์ขนาด 3×3×3 แทน โดยกติกาการชนะยังเหมือนเดิมคือใครวางตัวเองเรียงกันในแนวตรง 3 ช่องก่อนก็ชนะ

ข้อดีอย่างหนึ่งของ XO แบบ 3×3×3 ก็คือ เราสามารถพิสูจน์ได้ว่า มันจะไม่มีวันจบด้วยการเสมอ ซึ่งฟังดูดีมาก เพราะเกมน่าจะไม่น่าเบื่ออีกต่อไปแล้ว แต่เปล่าเลย เพราะเกมนี้มันมีวิธีที่ทำให้คนเริ่มก่อนชนะได้ตลอด เพียงคนเริ่มก่อนเริ่มต้นจากการลงที่ตำแหน่งกลางของลูกบาศก์ และเล่นอย่างไม่พลาด เขาจะสามารถบังคับเกมให้ตัวเองชนะได้ทุกครั้ง
ดังนั้นมันจึงน่าเบื่ออีกเช่นกัน เพราะถ้าทั้งสองคนเก่งพอ เรารู้ผลตั้งแต่ยังไม่เริ่มเล่นเลย
เพื่อจะแก้ปัญหานี้ บางคนจึงเสนอให้เปลี่ยนขนาดกระดานจาก 3×3×3 ไปเป็น 4×4×4 แล้วเปลี่ยนเงื่อนไขการชนะจากเรียง 3 ตัวเป็น เรียง 4 ตัว แทน แบบนี้น่าจะช่วยลดความได้เปรียบของผู้เริ่มก่อนลง เพราะไม่มีจุดกลางที่ได้เปรียบเกินไปแล้ว

มีใครอยากลองเล่นไหมฮะ แวะไปเล่นก่อน แล้วค่อยกลับมาอ่านต่อก็ได้ https://www.3dttt.app/
เหมือนจะฟังดูดีขึ้น แต่ความจริงคือ 4×4×4 ก็ยังไม่เวิร์กอยู่ดี เพราะถ้าทั้งคู่เล่นไม่พลาดเลย ก็ยังพบว่ามีวิธีที่ผู้เล่นที่เริ่มก่อนจะชนะได้เสมออยู่ดี
มาถึงตรงนี้ เราจะเห็นว่า ไม่ว่าจะเป็น XO ในสองมิติอย่าง 3×3 หรือในสามมิติอย่าง 3×3×3 และ 4×4×4 ทุกแบบล้วนมีจุดจบที่ล็อกผลไว้แล้ว คือมีไม่จบด้วยการเสมอ ก็จบแบบที่คนแรกชนะแน่นอน
คำถามคือ แล้วถ้าเริ่มเพิ่มขนาดหรือเพิ่มมิติขึ้นไปอีกล่ะจะเป็นยังไง
ความเจ๋งก็คือ เราสามารถพิสูจน์ได้ว่า สำหรับเกม XO ขนาด n ช่องใน k มิติใด ๆ ก็ตาม ผลลัพธ์ของเกมมีเพียงสองแบบเท่านั้นคือ จบที่เสมอ หรือจบที่ผู้เล่นคนแรกชนะแน่นอน เป็นไปได้แค่สองแบบเท่านั้น หรือแปลไทยเป็นไทยคือ เราไม่มีทางที่เราจะมีเกม XO ที่ ทั้งสองฝ่ายจะผลัดกันแพ้ชนะได้อย่างเท่าเทียมด้วยฝีมือได้จริง ๆ
ยิ่งไปกว่านั้น ยังมีทฤษฎีบททางคณิตศาสตร์ที่บอกว่า สำหรับ XO ขนาด n ช่องใด ๆ ก็ตาม มันจะมีจำนวนมิติ kₙ ที่ทำให้เกม XO ในมิตินั้นกลายเป็นเกมที่คนเริ่มก่อนชนะทุกครั้ง ได้อีกด้วย ทฤษฎีนี้ชื่อว่า Hales–Jewett Theorem ซึ่งเป็นหนึ่งในผลลัพธ์ที่น่าทึ่งในแขนงหนึ่งของวิชา Combinatoric ที่ชื่อว่า Ramsey Theory
จุดอ่อนสำคัญของ Hales–Jewett Theorem ก็คือ มันบอกแค่ว่า สำหรับเกมใน n ช่องใด ๆ ก็ตาม มันจะมีจำนวนมิติ kₙ ที่ทำให้เกมจบด้วยการเสมอ แต่ตัวทฤษฎีไม่ได้บอกว่าจะหาจำนวนมิติ kₙ ที่ว่านั้นยังไง และไม่ได้บอกด้วยว่า ก่อนหน้าจะถึง kₙ นั้น เกม XO ในมิติก่อนหน้าจะจบแบบกรณีไหน
ตารางด้านล่างแสดงจุดจบของเกม XO สำหรับ n และ k ต่าง ๆ โดย D หมายถึงจบด้วยการเสมอ W จบด้วยการที่คนเริ่มก่อนชนะแน่นอน และเครื่องหมาย ? แสดงให้เห็นว่าน่าจะเป็นแบบนั้นแต่ยังพิสูจน์ไม่ได้
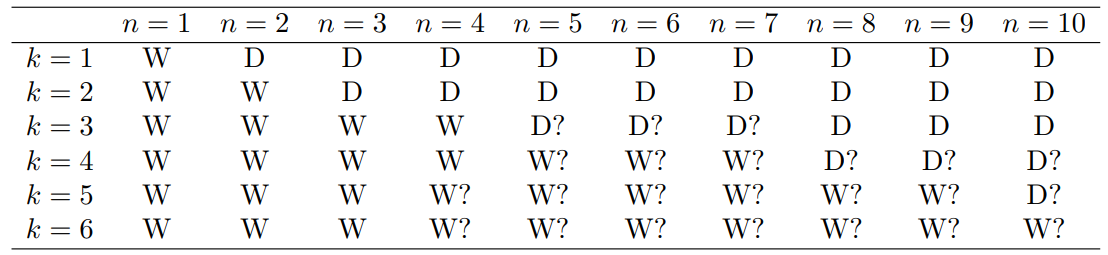
งานที่วิจัยที่ผมอ้างอิงนี้นั้นจริง ๆ ก็เก่าแล้ว ไม่แน่ใจเหมือนกันว่ามี ? ตัวไหนที่พิสูจน์ได้บ้างแล้วหรือยัง ผมพยายามหางานที่อัพเดทกว่าแต่ก็ไม่เจอ ใครที่เจอสามารถเอามาแชร์กันได้นะฮะ
สรุปก็คือ แม้ว่าสุดท้ายเราจะสรุปได้ว่าเกม XO นั้นน่าเบื่อมาก ๆ ในฐานะของเกม แต่ในเชิงคณิตศาสตร์เหมือนมันจะไม่น่าเบื่อเท่าไร การตั้งคำถามเกี่ยวกับมันให้ลึกซึ้งก็พาเราไปสู่คำถามที่น่าสนใจมากมาย ทั้งที่ถูกหาคำตอบได้แล้ว และที่ยังคงเป็นปริศนาของโลกนี้อยู่
และเช่นเดิม ใครที่อยากสนับสนุนเพจเว็บไซต์ของเรา ให้ผลิตคอนเทนต์คณิตศาสตร์แบบนี้ต่อไป ก็สามารถสมัครเป็นสมาชิกรายเดือนได้โดยกดปุ่ม 'สมัครสมาชิก' ได้เลยนะฮะ
เอกสารอ้างอิง
https://opentext.uleth.ca/Ramsey/sec_Intro.html
https://users.monash.edu/~normd/documents/Mathellaneous-05.pdf
https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=71b4da2401ff266ffb4c53712f9a63f6a509292f
https://www.youtube.com/watch?v=FwJZa-helig